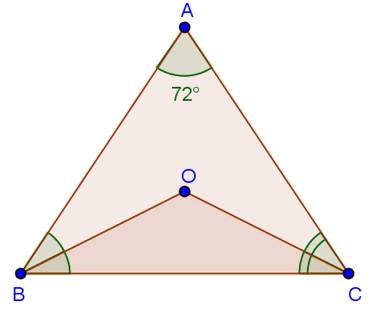
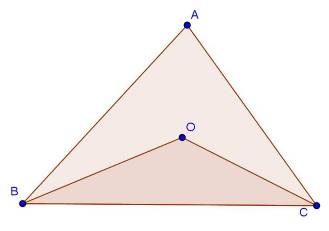
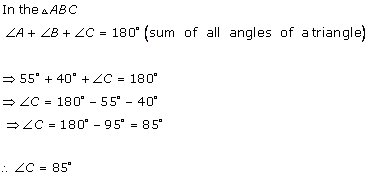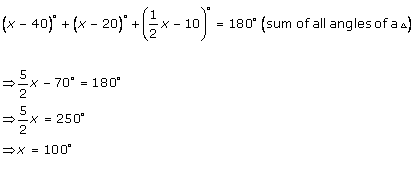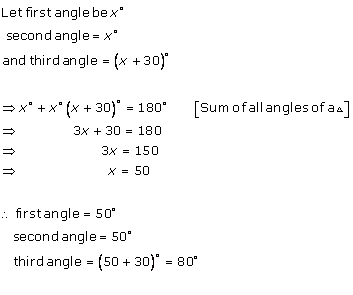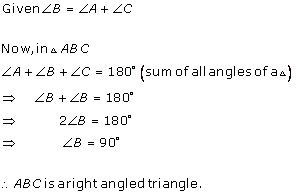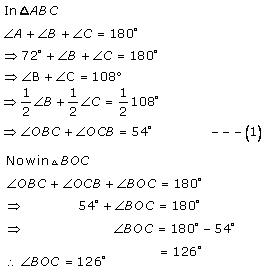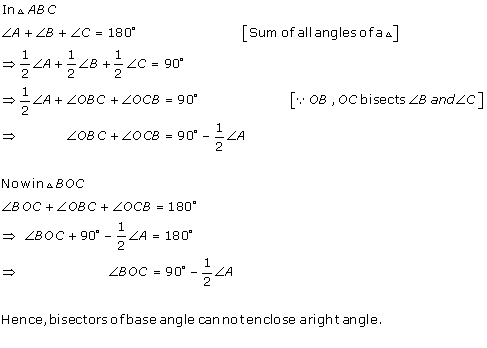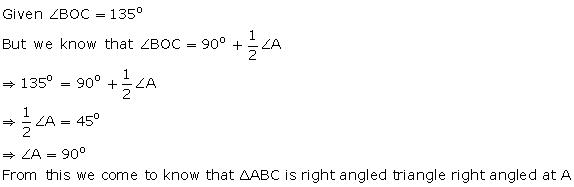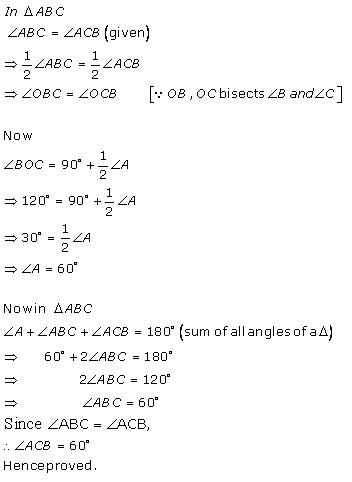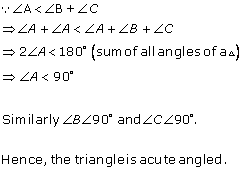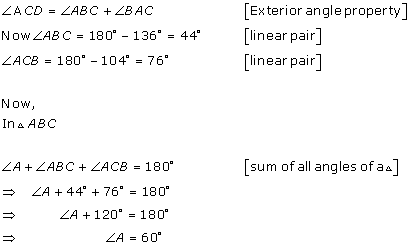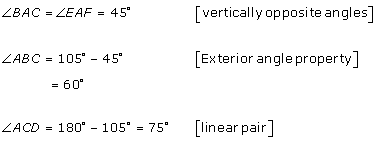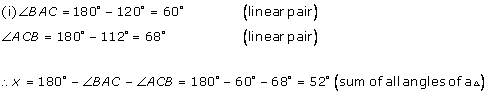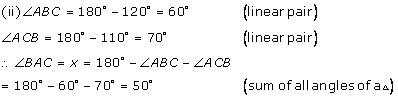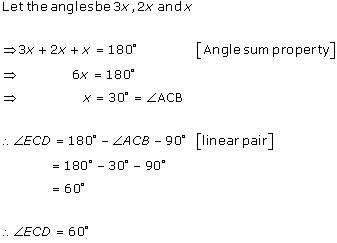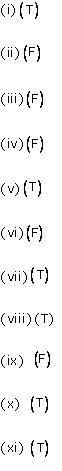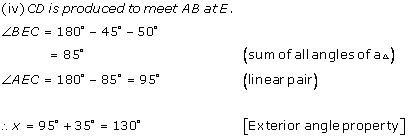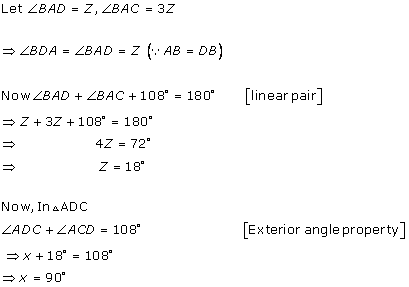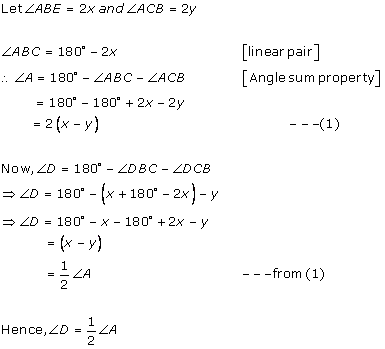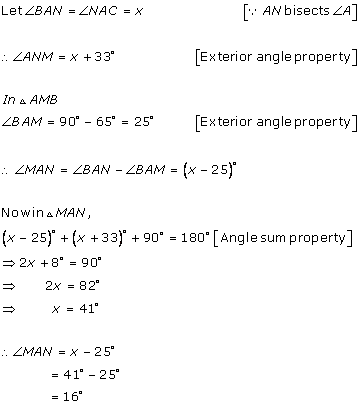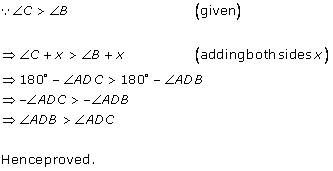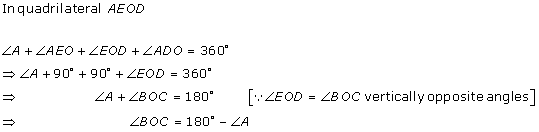Class 9 RD SHARMA Solutions Maths Chapter 11 - Triangle and its Angles
Triangle and its Angles Exercise Ex. 11.1
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
(i) No
As two right angles would sum up to 180o, and we know that the sum of all three angles of a triangle is 180o, so the third angle will become zero. This is not possible, so a triangle cannot have two right angles.
(ii) No
A triangle cannot have 2 obtuse angles, since then the sum of those two angles will be greater than 180o which is not possible as the sum of all three angles of a triangle is 180o.
(iii) Yes
A triangle can have 2 acute angles.
(iv) No
The sum of all the internal angles of a triangle is 180o. Having all angles more than 60o will make that sum more than 180o, which is impossible.
(v) No
The sum of all the internal angles of a triangle is 180o. Having all angles less than 60o will make that sum less than 180o, which is impossible.
(vi) Yes
The sum of all the internal angles of a triangle is 180o. So, a triangle can have all angles as 60o. Such triangles are called equilateral triangles.
Solution 7

Solution 8
Solution 9
Solution 10
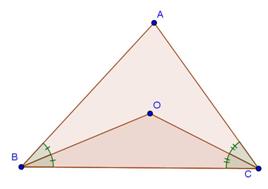
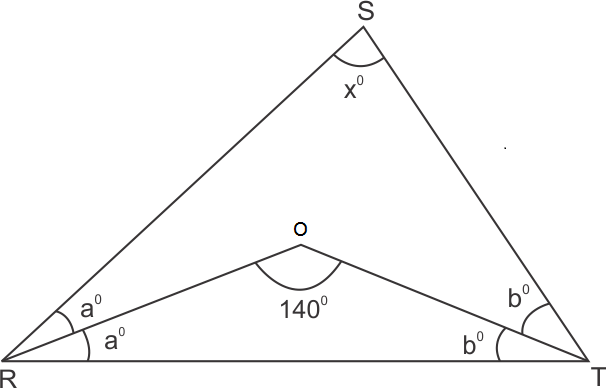
Solution 11
Solution 12
Triangle and its Angles Exercise Ex. 11.2
Solution 1
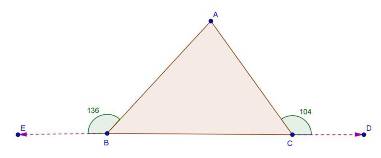
Solution 2
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
Solution 4
![]()
Solution 5
Solution 6
Solution 7
(i) 180o
(ii) interior
(iii) greater
(iv) one
(v) one
Solution 8

Solution 9
Solution 10
Solution 11
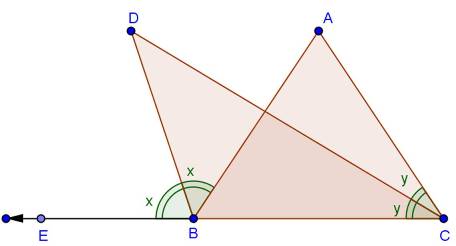
Solution 12
Solution 13
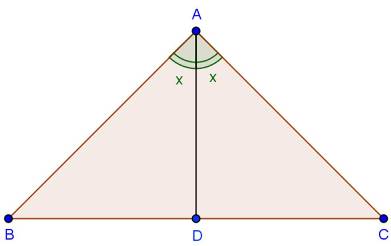
Solution 14
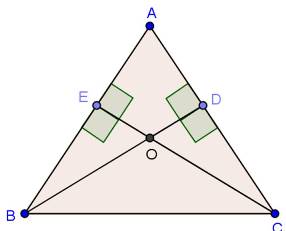
Solution 15
Triangle and its Angles Exercise 11.25
Solution 1
Let the measure of each angle be x°.
Now, the sum of all angles of any triangle is 180°.
Thus, x° + x° + x° = 180°
i.e. 3x° = 180°
i.e. x° = 60°
Hence, correct option is (c).
Solution 2
Let the measure of each acute angle of a triangle be x°.
Then, we have
x° + x° + 90° = 180°
i.e. 2x° = 90°
i.e. x° = 45°
Hence, correct option is (b).
Solution 3

Solution 4
Let the three angles of a triangle be A, B and C.
Now, A + B + C = 180°
If A = B + C
Then A + (A) = 180°
i.e. 2A = 180°
i.e. A = 90°
Since, one of the angle is 90°, the triangle is a Right triangle.
Hence, correct option is (d).
Solution 5

Solution 6
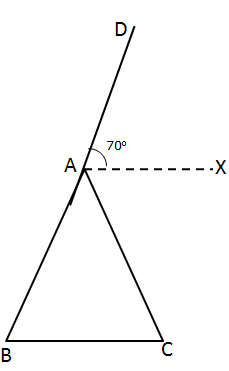

Solution 7

Solution 8
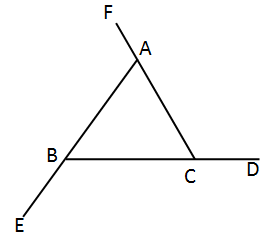

Solution 9


Solution 10


Solution 11
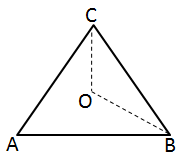

Solution 12
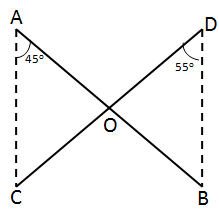

Triangle and its Angles Exercise 11.26
Solution 13

Solution 14

Solution 15

Solution 16

Triangle and its Angles Exercise 11.27
Solution 17

Solution 18


Solution 19
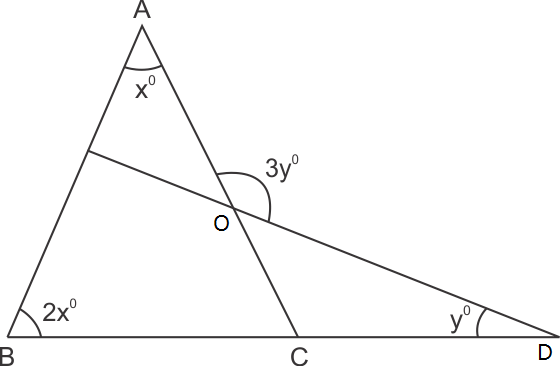

Solution 20

Triangle and its Angles Exercise 11.28
Solution 21
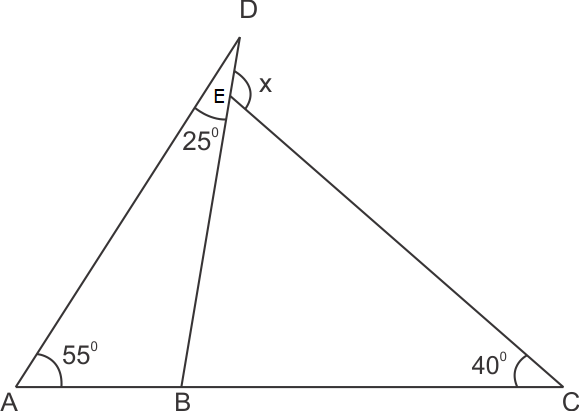

Solution 22
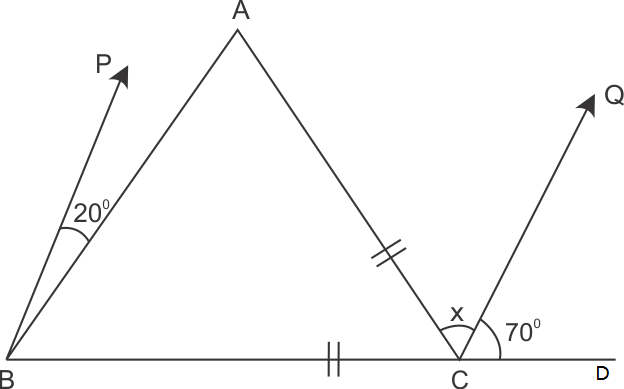

Solution 23
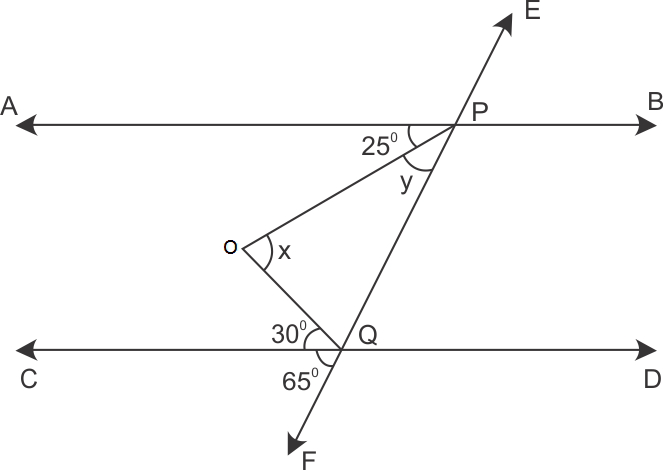

Solution 24
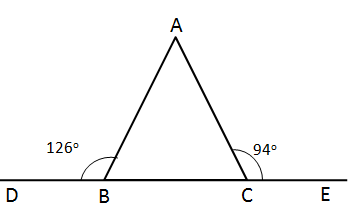

Triangle and its Angles Exercise 11.29
Solution 25
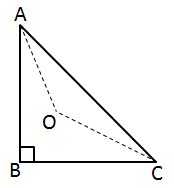

Solution 26
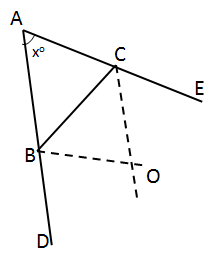

Solution 27
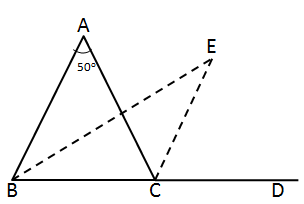

Solution 28
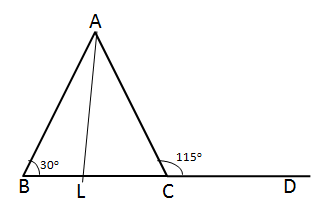

Solution 29


Solution 30