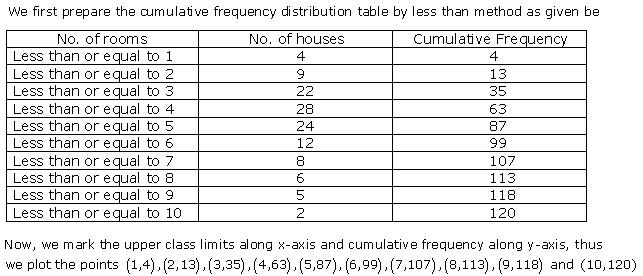
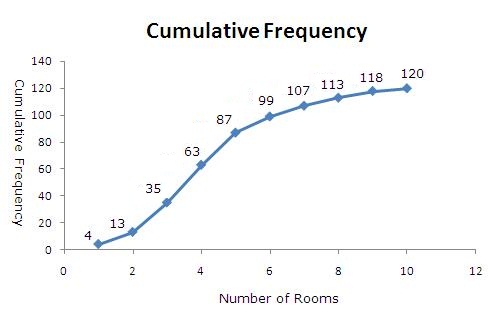
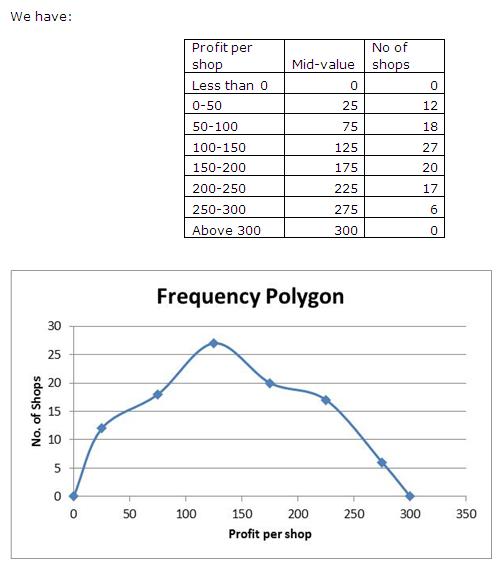
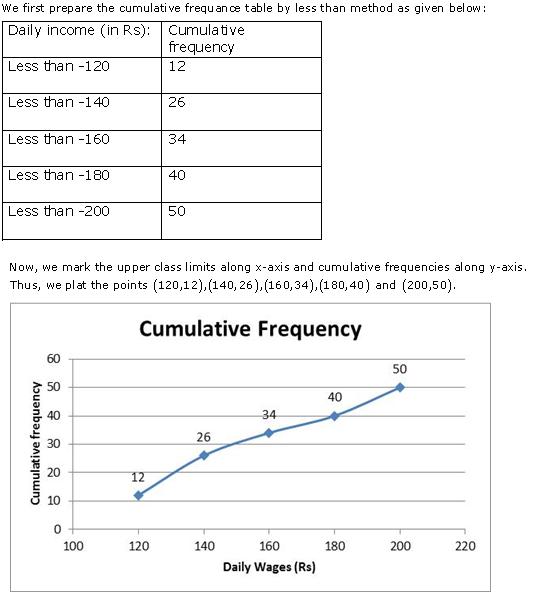
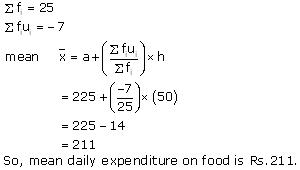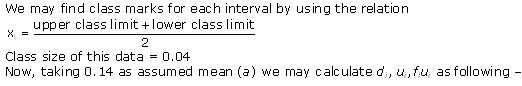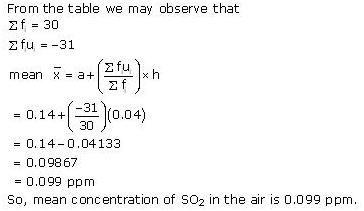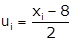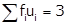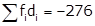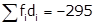Class 10 RD SHARMA Solutions Maths Chapter 15 - Statistics
Statistics Exercise Ex. 15.1
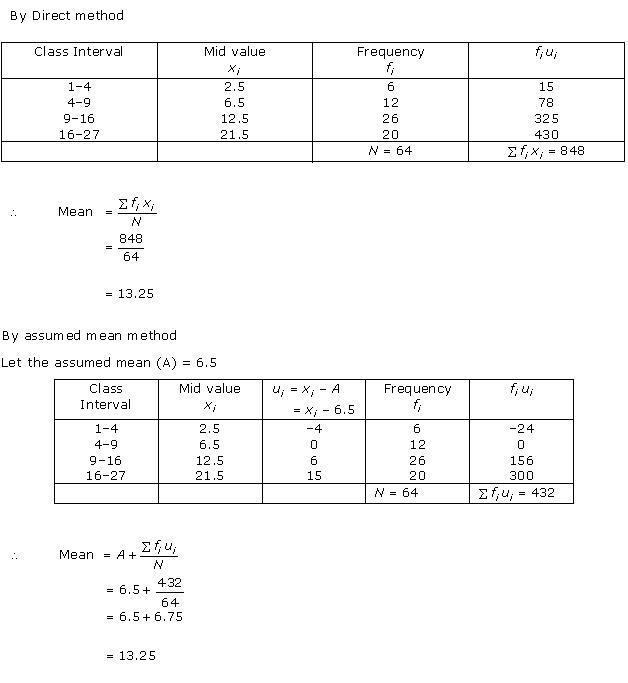
Solution 1
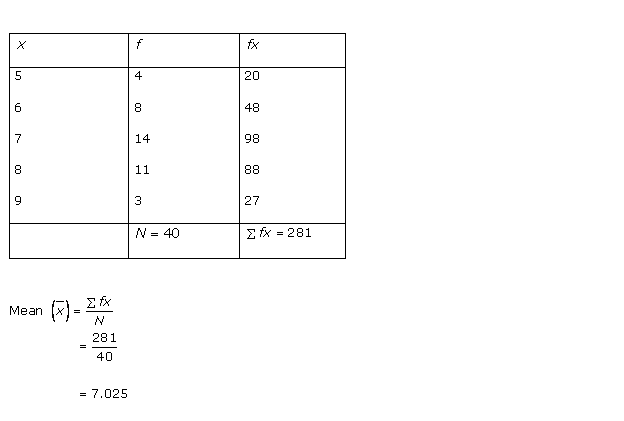
Solution 2
Solution 3
Solution 4
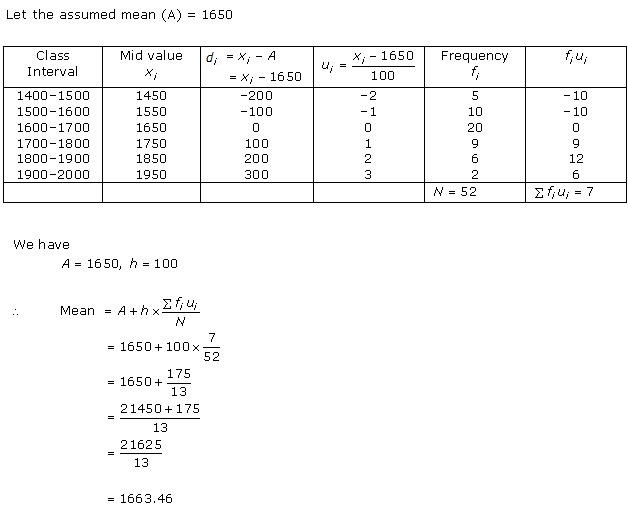
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
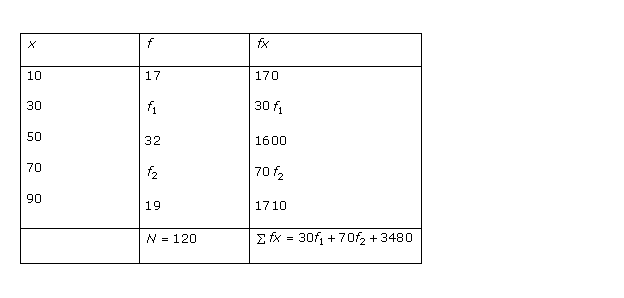
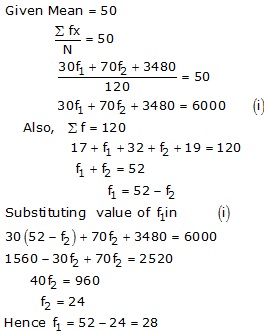
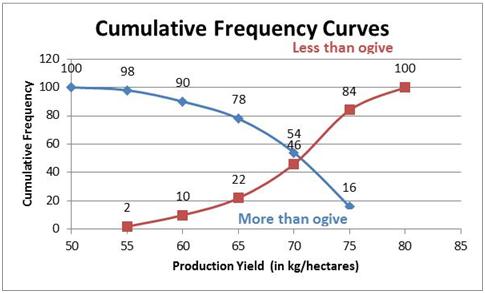
Statistics Exercise Ex. 15.2
Solution 1
Solution 2
Solution 3
Solution 4
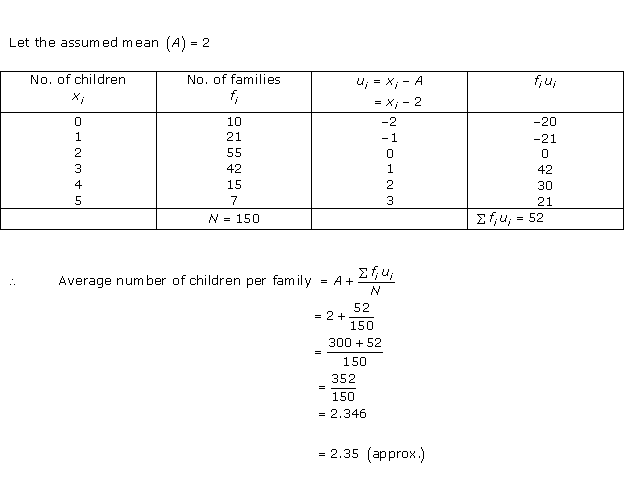
Solution 5
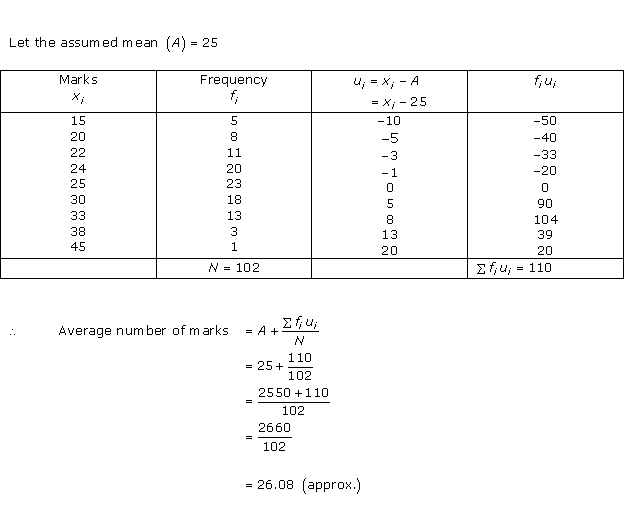
Solution 6
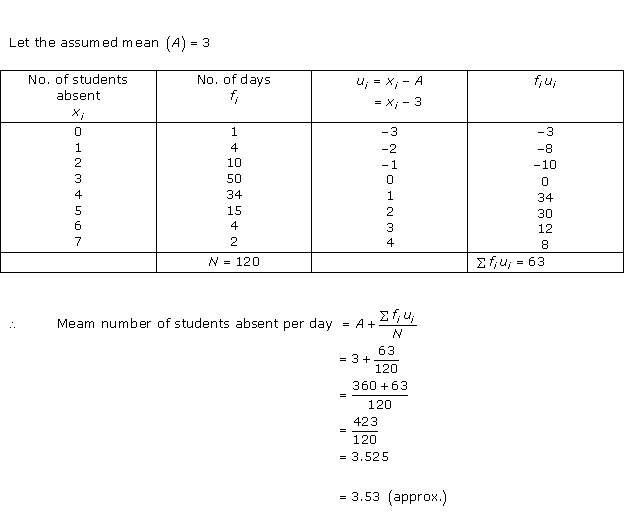
Solution 7
Solution 8
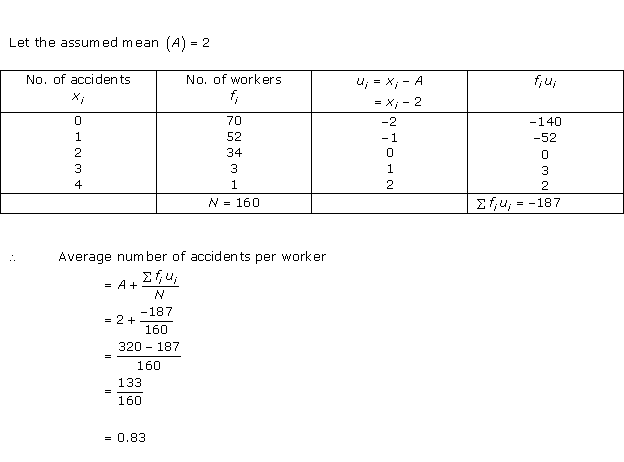
Solution 9
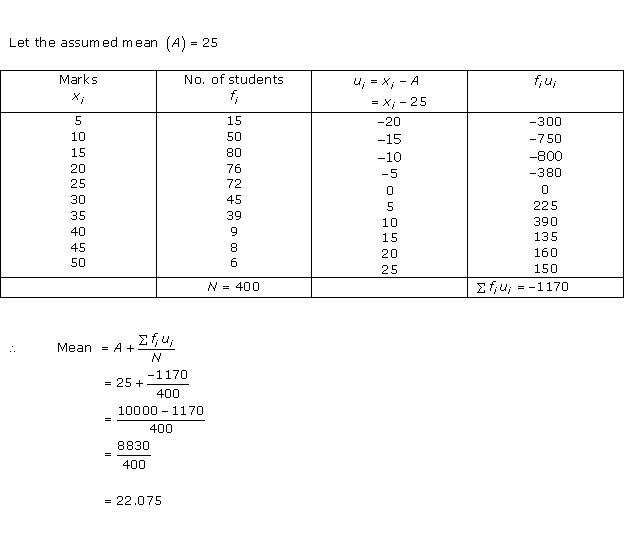
Statistics Exercise Ex. 15.3
Solution 1
Solution 2
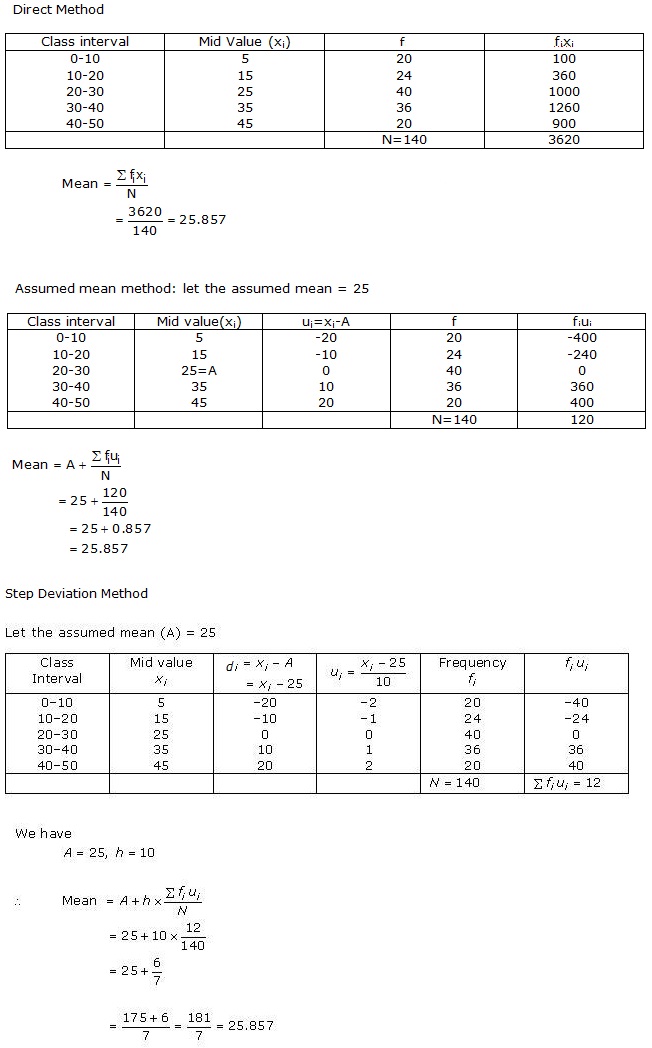
Let us find class marks (xi) for each interval by using the relation. 
Now we may compute xi and fixias following
| Number of plants | Number of houses (fi) | xi | fixi |
| 0 - 2 | 1 | 1 | 1 x 1 = 1 |
| 2 - 4 | 2 | 3 | 2 x 3 = 6 |
| 4 - 6 | 1 | 5 | 1 x 5 = 5 |
| 6 - 8 | 5 | 7 | 5 x 7 = 35 |
| 8 - 10 | 6 | 9 | 6 x 9 = 54 |
| 10 - 12 | 2 | 11 | 2 x 11 = 22 |
| 12 - 14 | 3 | 13 | 3 x 13 = 39 |
| Total | 20 | 162 |
From the table we may observe that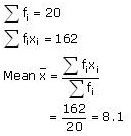 
So, mean number of plants per house is 8.1.
We have used here direct method as values of class marks (xi) and fi are small.
Solution 3
Solution 4
We may find class mark of each interval (xi) by using the relation. 
Class size h of this data = 3
Now taking 75.5 as assumed mean (a) we may calculate di, ui, fiui as following.
| Number of heart beats per minute | Number of women fi | xi | di = xi -75.5 |  |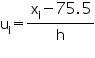
fiui |
| 65 - 68 | 2 | 66.5 | - 9 | - 3 | - 6 |
| 68 - 71 | 4 | 69.5 | - 6 | - 2 | - 8 |
| 71 - 74 | 3 | 72.5 | - 3 | - 1 | - 3 |
| 74 - 77 | 8 | 75.5 | 0 | 0 | 0 |
| 77 - 80 | 7 | 78.5 | 3 | 1 | 7 |
| 80 - 83 | 4 | 81.5 | 6 | 2 | 8 |
| 83 - 86 | 2 | 84.5 | 9 | 3 | 6 |
| Total | 30 | 4 |
Now we may observe from table that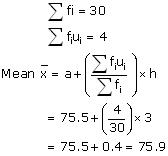 
So mean hear beats per minute for these women are 75.9 beats per minute.
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
| Number of mangoes | Number of boxes fi |
| 50 - 52 | 15 |
| 53 - 55 | 110 |
| 56 - 58 | 135 |
| 59 - 61 | 115 |
| 62 - 64 | 25 |
We may observe that class intervals are not continuous. There is a gap of 1 between two class intervals. So we have to add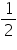 
to upper class limit and subtract from lower class limit of each interval.
And class mark (xi) may be obtained by using the relation 
Class size (h) of this data = 3
Now taking 57 as assumed mean (a) we may calculate di, ui, fiui as follows:
| Class interval | fi | xi | di = xi - 57 |  |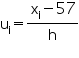
fiui |
| 49.5 - 52.5 | 15 | 51 | -6 | -2 | -30 |
| 52.5 - 55.5 | 110 | 54 | -3 | -1 | -110 |
| 55.5 - 58.5 | 135 | 57 | 0 | 0 | 0 |
| 58.5 - 61.5 | 115 | 60 | 3 | 1 | 115 |
| 61.5 - 64.5 | 25 | 63 | 6 | 2 | 50 |
| Total | 400 | 25 |
Now, we have: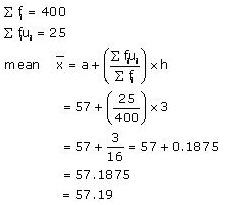
Clearly mean number of mangoes kept in a packing box is 57.19.
Note: We have chosen step deviation method here as values of fi, di are big and also there is a common multiple between all di.
Solution 22
We may calculate class mark (xi) for each interval by using the relation 
Class size = 50
Now taking 225 as assumed mean (a) we may calculate di, ui, fiui as follows:
| Daily expenditure (in Rs) | fi | xi | di = xi - 225 |  |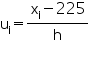
fiui |
| 100 - 150 | 4 | 125 | -100 | -2 | -8 |
| 150 - 200 | 5 | 175 | -50 | -1 | -5 |
| 200 - 250 | 12 | 225 | 0 | 0 | 0 |
| 250 - 300 | 2 | 275 | 50 | 1 | 2 |
| 300 - 350 | 2 | 325 | 100 | 2 | 4 |
| Total | -7 |
Now we may observe that - 
Solution 23
| Concentration of SO2 (in ppm) | Frequency | Class mark xi | di = xi - 0.14 |  |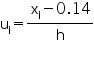
fiui |
| 0.00 - 0.04 | 4 | 0.02 | -0.12 | -3 | -12 |
| 0.04 - 0.08 | 9 | 0.06 | -0.08 | -2 | -18 |
| 0.08 - 0.12 | 9 | 0.10 | -0.04 | -1 | -9 |
| 0.12 - 0.16 | 2 | 0.14 | 0 | 0 | 0 |
| 0.16 - 0.20 | 4 | 0.18 | 0.04 | 1 | 4 |
| 0.20 - 0.24 | 2 | 0.22 | 0.08 | 2 | 4 |
| Total | 30 | -31 |
Solution 25
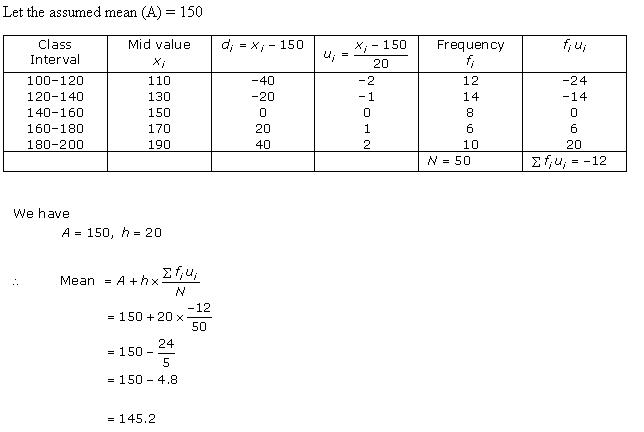
We may find class marks by using the relation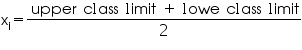 
Class size (h) for this data = 10
Now taking 70 as assumed mean (a) we may calculate di, ui, and fiui as follows:
Literacy rate (in %) |
Number of cities fi |
xi |
di= xi - 70 |
ui =di/10 |
fiui |
45 - 55 |
3 |
50 |
-20 |
-2 |
-6 |
55 - 65 |
10 |
60 |
-10 |
-1 |
-10 |
65 - 75 |
11 |
70 |
0 |
0 |
0 |
75 - 85 |
8 |
80 |
10 |
1 |
8 |
85 - 95 |
3 |
90 |
20 |
2 |
6 |
Total |
35 |
-2 |
Now we may observe that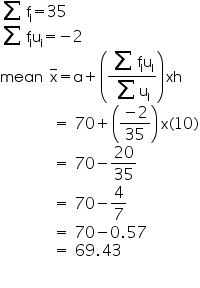 
So, mean literacy rate is 69.43%.
Solution 26
Here, we have cumulative frequency distribution less than type. First we convert it into an ordinary frequency distribution.
Solution 27
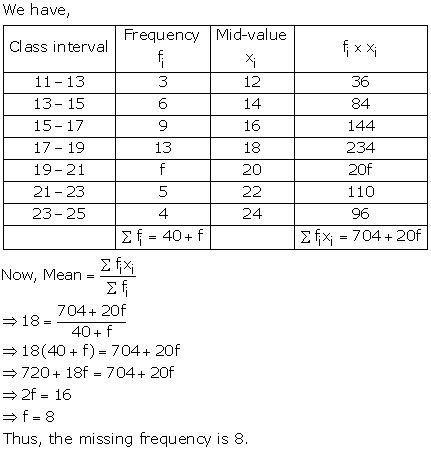
Solution 28
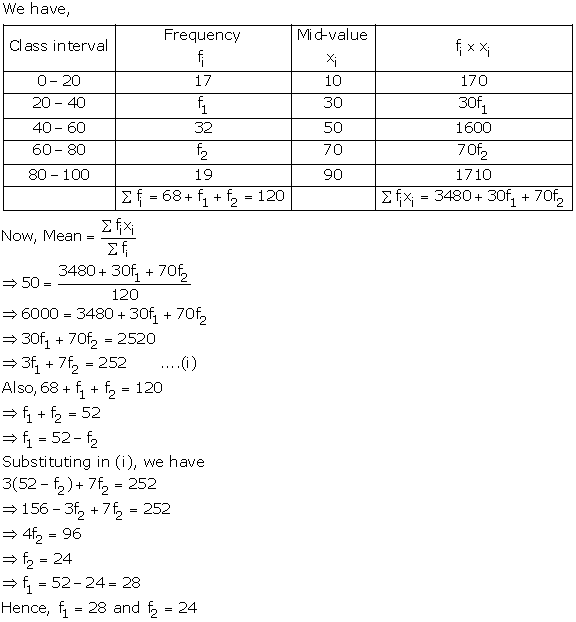
Solution 29
Solution 5
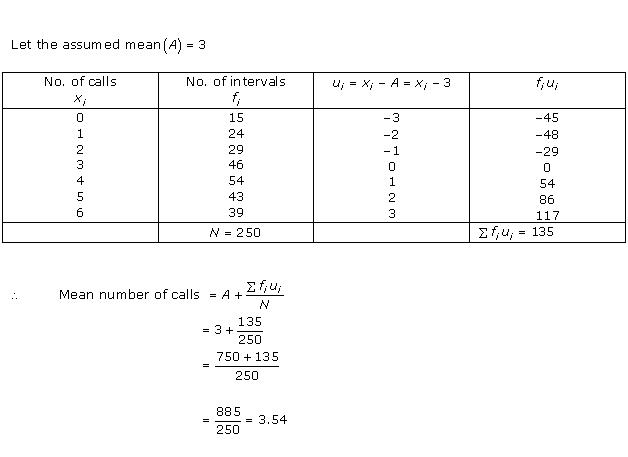
Let the assumed mean be A = 8
Here, h = 2
|
Class interval |
Mid value xi |
di = xi - 8 |
|
fi |
fiui |
|
3 - 5 5 - 7 7 - 9 9 - 11 11 - 13 |
4 6 8 10 12 |
-4 -2 0 2 4 |
-2 -1 0 1 2 |
5 10 10 7 8 |
-10 -10 0 7 16 |
|
|
|
|
|
N = 40 |
|
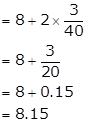
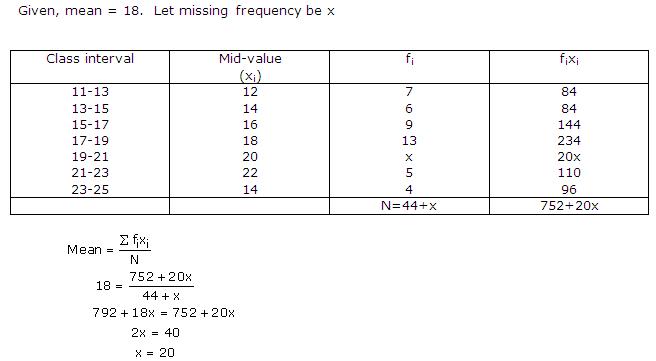
Solution 24 (i)
We may find class mark of each interval by using the relation
|
Number of days |
Number of students fi |
xi |
di = xi - 21 |
fidi |
|
0 - 6 6 - 12 12 - 18 18 - 24 24 - 30 30 - 36 36 - 42 |
10 11 7 4 4 3 1 |
3 9 15 21 27 33 39 |
-18 -12 -6 0 6 12 18 |
-180 -132 -42 0 24 36 18 |
|
|
40 |
|
|
|
Assumed mean A = 21
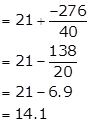
Hence, the number of days a student was absent is 14.1.
Solution 30
We may find class mark of each interval by using the relation
|
Marks |
Number of students fi |
xi |
di = xi - 47.5 |
fidi |
|
30 - 35 35 - 40 40 - 45 45 - 50 50 - 55 55 - 60 60 - 65 |
14 16 28 23 18 8 3 |
32.5 37.5 42.5 47.5 52.5 57.5 62.5 |
-15 -10 -5 0 5 10 15 |
-210 -160 -140 0 90 80 45 |
|
|
110 |
|
|
|
Assumed mean A = 47.5
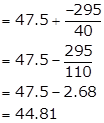
Hence, mean marks of the students is 44.81.
Statistics Exercise Ex. 15.4
Solution 1
Solution 2
The median height of the students is Rs 167.13.
Solution 3
Solution 5
Solution 6
Solution 7
Solution 8
We can find cumulative frequencies with their respective class intervals as below -
Life time |
Number of lamps (fi) |
Cumulative frequency |
1500 - 2000 |
14 |
14 |
2000 - 2500 |
56 |
14 + 56 = 70 |
2500 - 3000 |
60 |
70 + 60 = 130 |
3000 - 3500 |
86 |
130 + 86 = 216 |
3500 - 4000 |
74 |
216 + 74 = 290 |
4000 - 4500 |
62 |
290 + 62 = 352 |
4500 - 5000 |
48 |
352 + 48 = 400 |
Total (n) |
400 |
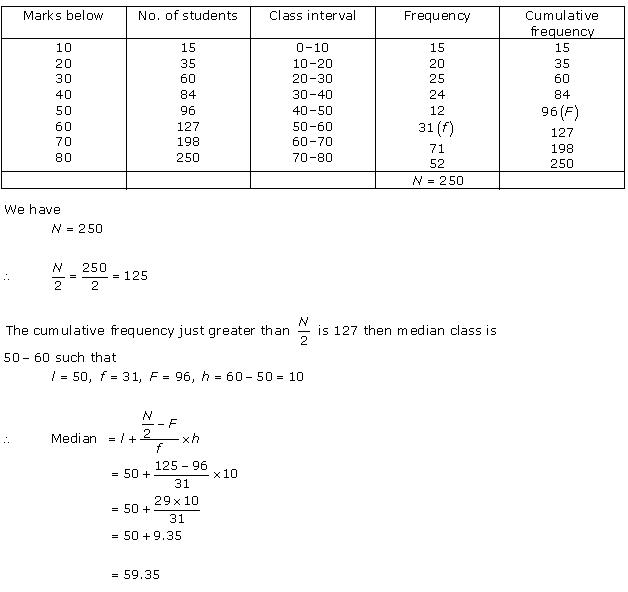
Now we may observe that cumulative frequency just greater than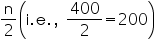 
is 216 belonging to class interval 3000 - 3500.
Median class = 3000 - 3500
Lower limit (l) of median class = 3000
Frequency (f) of median class = 86
Cumulative frequency (cf) of class preceding median class = 130
Class size (h) = 500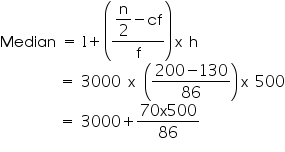 
So, median life time of lamps is 3406.98 hours.
Solution 9
We may find cumulative frequencies with their respective class intervals as below
| Weight (in kg) | 40 - 45 | 45 - 50 | 50 - 55 | 55 - 60 | 60 - 65 | 65 - 70 | 70 - 75 |
| Number of students (f) | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
| c.f. | 2 | 5 | 13 | 19 | 25 | 28 | 30 |
Cumulative frequency just greater than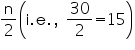 
is 19, belonging to class interval 55 - 60.
Median class = 55 - 60
Lower limit (l) of median class = 55
Frequency (f) of median class = 6
Cumulative frequency (cf) of median class = 13
Class size (h) = 5
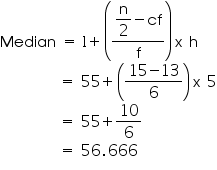
So, median weight is 56.67 kg.
Solution 10
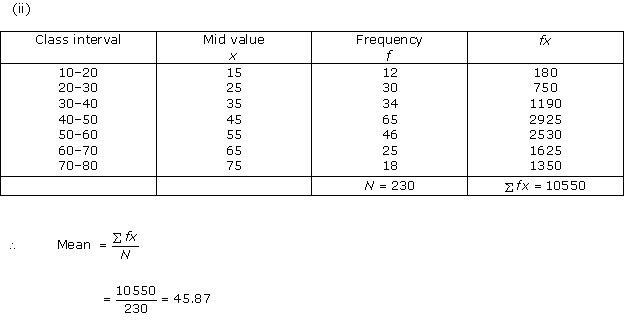
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15(i)
Solution 15(ii)
Solution 16
Solution 17
Here class width is not same. There is no need to adjust the frequencies according to class intervals. Now given frequency table is of less than type represented with upper class limits. As policies were given only to persons having age 18 years onwards but less than 60 years, we can define class intervals with their respective cumulative frequency as below
Age (in years) |
Number of policy holders (fi) |
Cumulative frequency (cf) |
18 - 20 |
2 |
2 |
20 - 25 |
6 - 2 = 4 |
6 |
25 - 30 |
24 - 6 = 18 |
24 |
30 - 35 |
45 - 24 = 21 |
45 |
35 - 40 |
78 - 45 = 33 |
78 |
40 - 45 |
89 - 78 = 11 |
89 |
| 45 - 50 | 92 - 89 = 3 |
92 |
50 - 55 |
98 - 92 = 6 |
98 |
55 - 60 |
100 - 98 = 2 |
100 |
Total (n) |
|
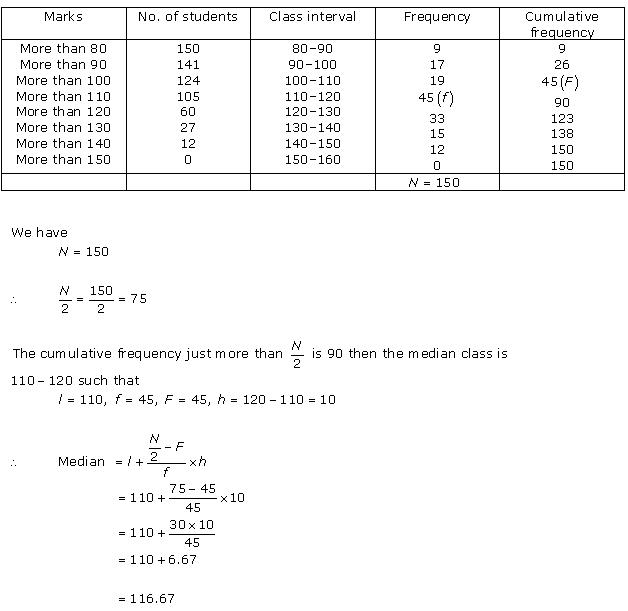
Now from table we may observe that n = 100.
Cumulative frequency (cf) just greater than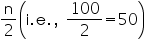 
is 78 belonging to interval 35 - 40
So, median class = 35 - 40
Lower limit (l) of median class = 35
Class size (h) = 5
Frequency (f) of median class = 33
Cumulative frequency (cf) of class preceding median class = 45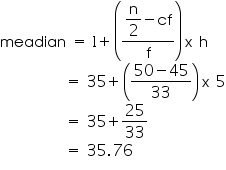 
So, median age is 35.76 years.
Solution 18
The given data is not having continuous class intervals. We can observe that difference between two class intervals is 1. So, we have to add and subtract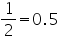 
to upper class limits and lower class limits.
Now continuous class intervals with respective cumulative frequencies can be represented as below:
Length (in mm) |
Number or leaves fi |
Cumulative frequency |
117.5 - 126.5 |
3 |
3 |
126.5 - 135.5 |
5 |
3 + 5 = 8 |
135.5 - 144.5 |
9
|
8 + 9 = 17 |
144.5 - 153.5 |
12 |
17 + 12 = 29 |
153.5 - 162.5 |
5
|
29 + 5 = 34 |
162.5 - 171.5 |
4 |
34 + 4 = 38 |
171.5 - 180.5 |
2 |
38 + 2 = 40 |
From the table we may observe that cumulative frequency just greater then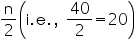 
is 29, belonging to class interval 144.5 - 153.5.
Median class = 144.5 - 153.5
Lower limit (l) of median class = 144.5
Class size (h) = 9
Frequency (f) of median class = 12
Cumulative frequency (cf) of class preceding median class = 17
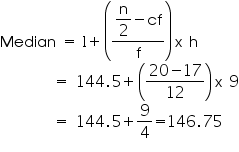
So, median length of leaves is 146.75 mm.
Solution 19
Solution 20
Solution 21
Solution 4
The cumulative frequency table is
|
Salary |
Frequency fi |
Cumulative frequency (c.f.) |
|
5 - 10 10 - 15 15 - 20 20 - 25 25 - 30 30 - 35 35 - 40 40 - 45 45 - 50 |
49 133 63 15 6 7 4 2 1 |
49 182 245 260 266 273 277 279 280 |
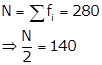
The cumulative frequency greater than and nearest to 140 is 182.
So, median class is 10 - 15
Lower limit (l) = 10, class size (h) = 5, c.f. = 49
Frequency of median class = 133
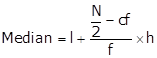
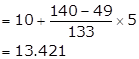
Hence, mean median salary is Rs. 13421.
Statistics Exercise Ex. 15.5
Solution 1
Solution 2
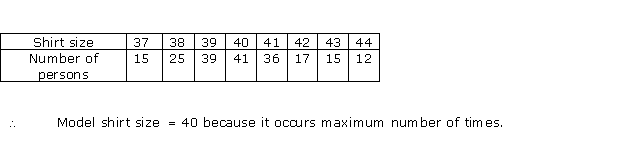
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
Solution 4
Solution 5
Solution 6
Solution 7
We may compute class marks (xi) as per the relation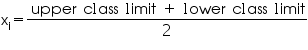
Now taking 30 as assumed mean (a) we may calculate di and fidi as follows.
Age (in years) |
Number of patients fi |
class mark xi |
di= xi - 30 |
fidi |
5 - 15 |
6 |
10 |
-20 |
-120 |
15 - 25 |
11 |
20 |
-10 |
-110 |
25 - 35 |
21 |
30 |
0 |
0 |
35 - 45 |
23 |
40 |
10 |
230 |
45 - 55 |
14 |
50 |
20 |
280 |
55 - 65 |
5 |
60 |
30 |
150 |
Total |
80 |
430 |
From the table we may observe that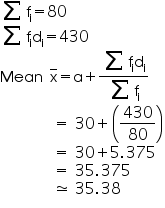 
Clearly, mean of this data is 35.38. It represents that on an average the age of a patient admitted to hospital was 35.38 years.
As we may observe that maximum class frequency is 23 belonging to class interval 35 - 45.
So, modal class = 35 - 45
Lower limit (l) of modal class = 35
Frequency (f1) of modal class = 23
Class size (h) = 10
Frequency (f0) of class preceding the modal class = 21
Frequency (f2) of class succeeding the modal class = 14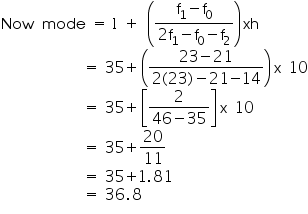 
Clearly mode is 36.8.It represents that maximum number of patients admitted in hospital were of 36.8 years.
Solution 8
From the data given as above we may observe that maximum class frequency is 61 belonging to class interval 60 - 80.
So, modal class = 60 - 80
Lower class limit (l) of modal class = 60
Frequency (f1) of modal class = 61
Frequency (f0) of class preceding the modal class = 52
Frequency (f2) of class succeeding the modal class = 38
Class size (h) = 20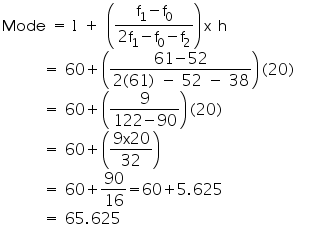 
So, modal lifetime of electrical components is 65.625 hours.
Solution 9
Solution 10
We may observe from the given data that maximum class frequency is 10 belonging to class interval 30 - 35.
So, modal class = 30 - 35
Class size (h) = 5
Lower limit (l) of modal class = 30
Frequency (f1) of modal class = 10
Frequency (f0) of class preceding modal class = 9
Frequency (f2) of class succeeding modal class = 3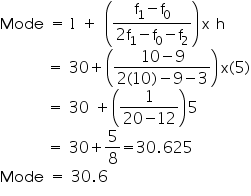 
It represents that most of states/U.T have a teacher - student ratio as 30.6
Now we may find class marks by using the relation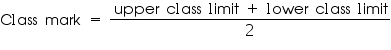 
Now taking 32.5 as assumed mean (a) we may calculate di, ui and fiui as following.
Number of students per teacher |
Number of states/U.T (fi) |
xi |
di = xi - 32.5 |
ui |
fiui |
15 - 20 |
3 |
17.5 |
-15 |
-3 |
-9 |
20 - 25 |
8 |
22.5 |
-10 |
-2 |
-16 |
25 - 30 |
9 |
27.5 |
-5 |
-1 |
-9 |
30 - 35 |
10 |
32.5 |
0 |
0 |
0 |
35 - 40 |
3 |
37.5 |
5 |
1 |
3 |
40 - 45 |
0 |
42.5 |
10 |
2 |
0 |
45 - 50 |
0 |
47.5 |
15 |
3 |
0 |
50 - 55 |
2 |
52.5 |
20 |
4
|
8 |
Total |
35
|
-23 |
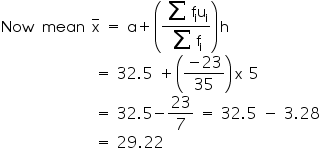
So mean of data is 29.2
It represents that on an average teacher - student ratio was 29.2.
Solution 11
Solution 12
From the given data we may observe that maximum class frequency is 20 belonging to 40 - 50 class intervals.
So, modal class = 40 - 50
Lower limit (l) of modal class = 40
Frequency (f1) of modal class = 20
Frequency (f0) of class preceding modal class = 12
Frequency (f2) of class succeeding modal class = 11
Class size = 10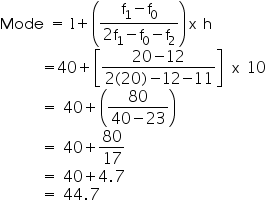 
So mode of this data is 44.7 cars.
Solution 13
Solution 14
Solution 15
Solution 16
We may observe from the given data that maximum class frequency is 40 belonging to 1500 - 2000 intervals.
So, modal class = 1500 - 2000
Lower limit (l) of modal class = 1500
Frequency (f1) of modal class = 40
Frequency (f0) of class preceding modal class = 24
Frequency (f2) of class succeeding modal class = 33
Class size (h) = 500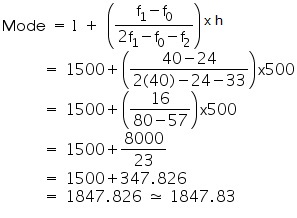 
So modal monthly expenditure was Rs. 1847.83
Now we may find class mark as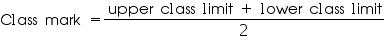 
Class size (h) of give data = 500
Now taking 2750 as assumed mean (a) we may calculate di, ui and fiui as follows:
Expenditure (in Rs) |
Number of families fi |
xi |
di = xi - 2750 |
ui |
fiui
|
1000 - 1500 |
24 |
1250 |
-1500 |
-3 |
-72 |
1500 - 2000 |
40 |
1750 |
-1000 |
-2 |
-80 |
2000 - 2500 |
33 |
2250 |
-500 |
-1
|
-33 |
2500 - 3000 |
28 |
2750 |
0 |
0 |
0 |
3000 - 3500 |
30 |
3250 |
500 |
1 |
30 |
3500 - 4000 |
22 |
3750 |
1000 |
2 |
44 |
4000 - 4500 |
16 |
4250 |
1500 |
3 |
48 |
4500 - 5000 |
7 |
4750 |
2000 |
4 |
28 |
Total |
200 |
-35 |
Now from table may observe that
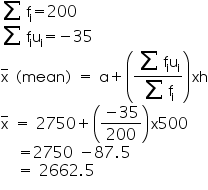
So, mean monthly expenditure was Rs. 2662.50.
Solution 17
From the given data we may observe that maximum class frequency is 18 belonging to class interval 4000 - 5000.
So, modal class = 4000 - 5000
Lower limit (l) of modal class = 4000
Frequency (f1) of modal class = 18
Frequency (f0) of class preceding modal class = 4
Frequency (f2) of class succeeding modal class = 9
Class size (h) = 1000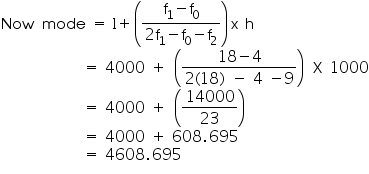 
So mode of given data is 4608.7 runs.
Solution 18
Solution 19
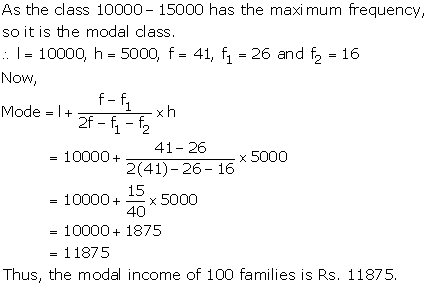
Solution 3 (iv)
The cumulative frequency table is
|
Salary |
Frequency fi |
|
0 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 60 - 70 |
8 10 10 16 12 6 7 |
Modal class is 30 - 40
Lower limit (l) = 30, class size (h) = 10, f = 16, f1 = 10 and f2 = 12
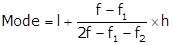
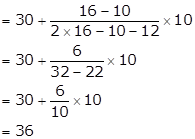
Hence, the mode is 36.
Statistics Exercise Ex. 15.6
Solution 1
Solution 2
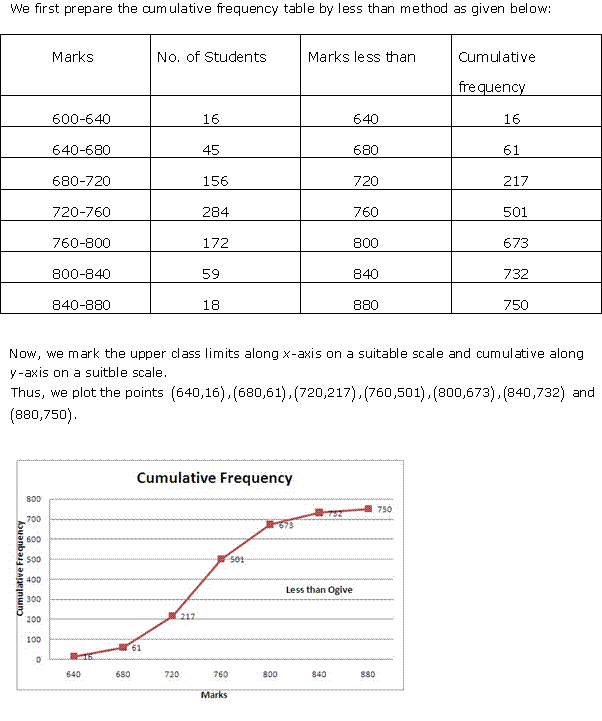
Solution 3
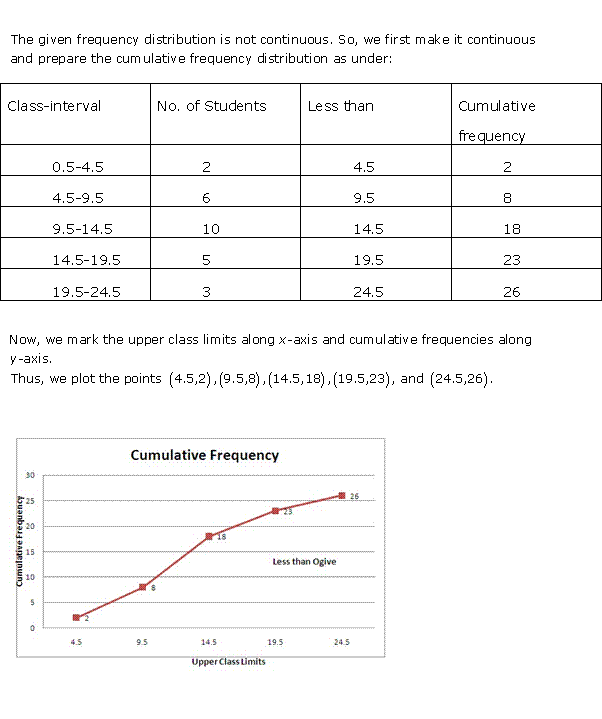
Solution 4
Solution 5
Solution 6
Solution 7
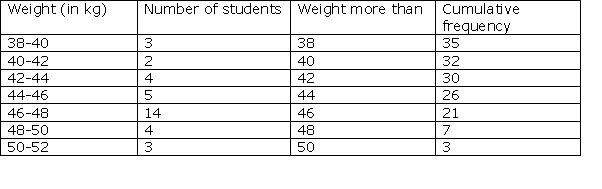
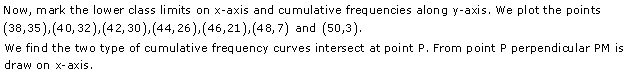
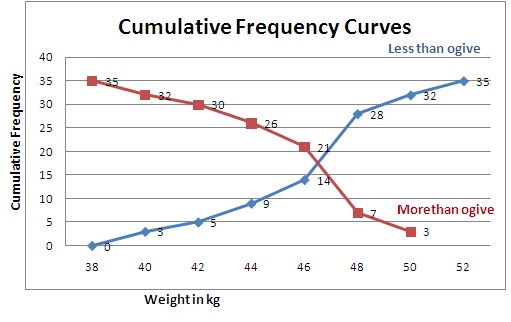
Solution 8
Less Than Series:
|
Class interval |
Cumulative Frequency |
|
Less than 10 |
22 |
|
Less than 20 |
32 |
|
Less than 30 |
40 |
|
Less than 40 |
55 |
|
Less than 50 |
60 |
|
Less than 60 |
66 |
We plot the points (10, 22), (20, 32), (30, 40), (40, 55), (50, 60) and (60, 66) to get 'less than type' ogive.
More Than Series:
|
Class interval |
Frequency |
|
More than 0 |
66 |
|
More than 10 |
44 |
|
More than 20 |
34 |
|
More than 30 |
26 |
|
More than 40 |
11 |
|
More than 50 |
6 |
We plot the points (0, 66), (10, 44), (20, 24), (30, 26), (40, 11), and (50, 6) to get more than ogive.
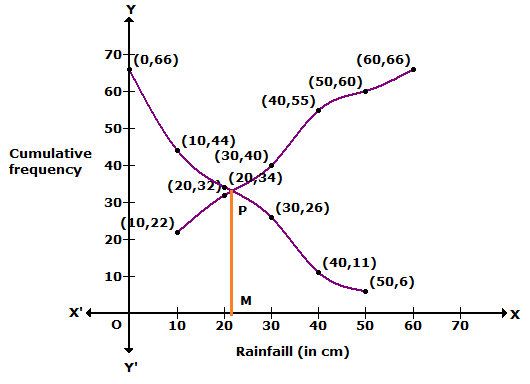
From the graph, median = 21.25 cm
Solution 9
More than type frequency distribution is given by
|
Class interval |
Frequency fi |
Cumulative frequency |
|
More than 20 More than 30 More than 40 More than 50 More than 60 More than 70 More than 80 |
10 8 12 24 6 25 15 |
100 90 82 70 46 40 15 |
So, more than type frequency curve is
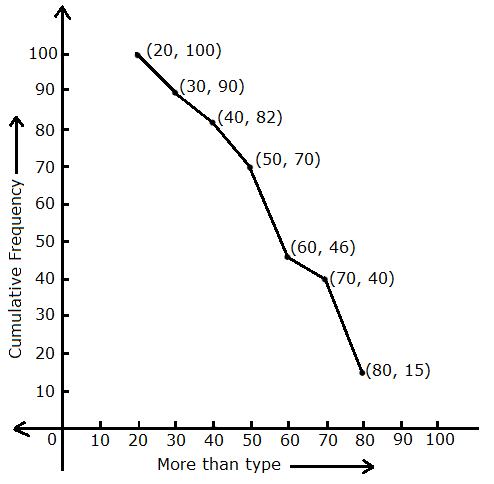
Solution 10
Less than type frequency distribution is given by
|
Class interval |
Frequency fi |
Cumulative frequency |
|
Less than 220 Less than 240 Less than 260 Less than 280 Less than 300 |
12 14 8 6 10 |
12 26 34 40 50 |
So, less than type frequency curve is
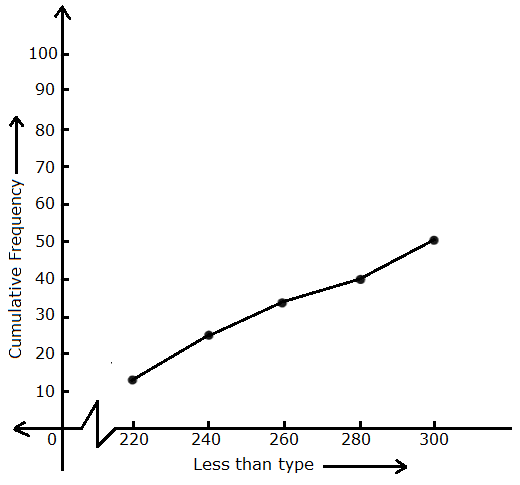
Statistics Exercise 15.66
Solution 1
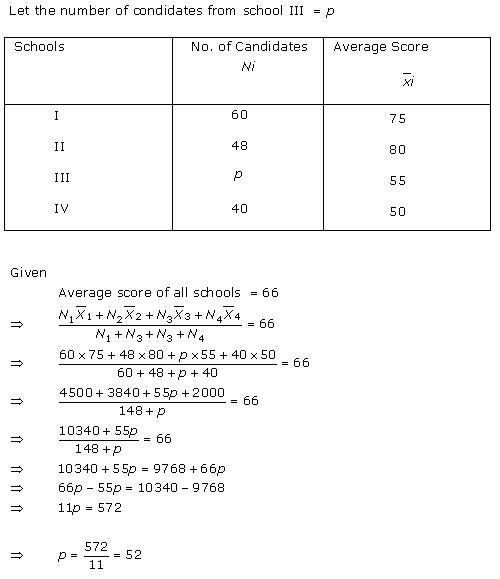
There are three main measure of central tendency the mode, the median and the mean.
Each of these measures describes a different indication of the typical or central value in the distribution.
The mode is the most commonly occuring value in a distribution.
Median is middle value of distribution.
While standard deviation is a measure of dispersion of a set of data from its mean.
So, the correct option is (d).
Solution 2
Solution 3
Solution 4
It is well known that relation between mean, median and mode 1 s
3 median = mode + 2 mean
Mode = 3 median - 2 mean
So, the correct option is (a).
Solution 5
Mean is an average value of any given data which cannot be determined by a graph.
Value of median and mode can easily be calculated by graph.
Median is middle value of a distribution and mode is highest frequent value of a given distribution.
So, the correct option is (a).
Solution 6
The median of a series may be determined through the graphical presentation of data in the forms of Ogives.
Ogive is a curve showing the cummulative frequency for a given set of data.
To get the median we present the data graphically in the form of 'less than' ogive or 'more than' ogive
Then the point of intersection of the two graphs gives the value of the median.
So, the correct option is (d).
Solution 7
Histogram is used to plot the distribution of numerical data or frequency of occurrences of data.
Mode is the most commonly occurring value in the data.
So in distribution or Histogram, the value of the x-coordinate corresponding to the peak value on y - axis, is the mode.
So, the correct option is (a).
Solution 8
Mode is the most frequent value in the data.
Mode is the value which occurs the most number of times.
So, the correct option is (c).
Solution 9
Solution 10
We know that the relation between mean, median & mode is
3 Median = Mode + 2 Mean
Hence, Mode = 3 Median - 2 Mean
So, the correct option is (c).
Statistics Exercise 15.67
Solution 11
Solution 12
We know that the relation between mean, median & mode is
3 Median = mode + 2 Mean
Hence, mode = 3 Median - 2 Mean
So, the correct option is (d).
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Mode is the number in observation data is that which repeats most number of time
In the given data 48 comes twice and 43 comes twice but mode is 43.
Hence if x = 43 then 43 comes thrice.
So x + 3 = 43 + 3 = 46
So, the correct option is (c).
Solution 19
In the given data 15, 16, 17 comes twice but given 15 is mode.
Hence 15 comes more than 16, 17.
This is only possible if x = 15.
So, the correct option is (a).
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Statistics Exercise 15.68
Solution 25
We know, 3 Median = Mode + 2 Mean
mean = 24
mode = 12
3 median = 12 + 2 × 24
= 12 + 48
= 60
median = 20
So, the correct option is (c).
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32
Solution 33
Solution 34
Solution 35
Solution 36
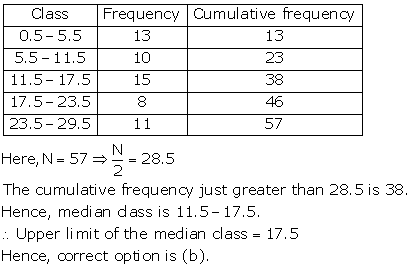
While computing the mean of the grouped data, we assume that the frequencies are centred at the class marks of the classes.
Hence, correct option is (b).
Solution 37
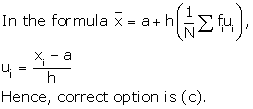
Statistics Exercise 15.69
Solution 38
Solution 39
Solution 40
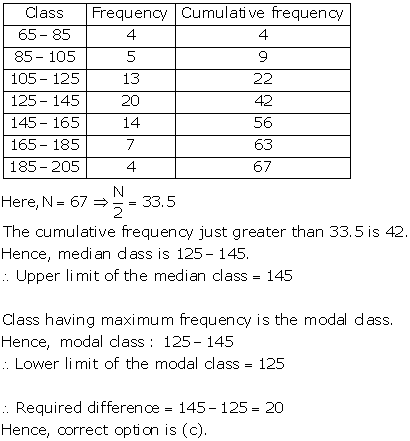
Solution 41
di's are the deviations from a of mid-points of classes.
Hence, correct option is (c).
Solution 42
The abscissa of the point of intersection of less than type and of the more than type cumulative frequency curves of a grouped data given its median.
Hence, correct option is (b).
Solution 43
