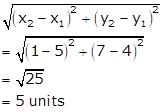Class 10 SELINA Solutions Maths Chapter 13 - Section and Mid-Point Formula
The Indian Certificate of Secondary Education Board emphasises academic excellence, holistic development, and practical application of student's knowledge, and hence it is recognised globally. The board aims to provide a well-rounded education with a curriculum that helps students develop a strong foundation, critical thinking, and problem-solving skills.
The ICSE Class 10 Math Chapter – Section and Midpoint formula is one of the most important concepts in Coordinate Geometry. They are used to find the coordinates of a point dividing a line segment or finding the midpoint of a line segment. Solving such problems allows students to understand the practical applications of the formulas and their significance in geometry.
Selina Solutions for Section and Midpoint Formula helps students prepare for their exams and future academic pursuits. They extensively cover the section and midpoint formulas and provide step-by-step explanations and solutions for each question in the textbook. Thus, students understand the underlying concepts and techniques required to apply the formulas. These solutions completely align with the ICSE exam pattern and marking scheme so that students can effectively prepare and improve their performance.
At TopperLearning, we aim to provide a comprehensive and personalised learning experience. We offer Selina Solutions for Classes 9 and 10 for Maths, Physics, Chemistry, and Biology. Designed by subject matter experts, these solutions enable students to grasp all challenging chapters in an easy manner. Our Ask a Doubt feature enables interactive learning that helps students clarify their doubts and improve their academic performance. In addition to that, we also offer a range of resources such as video lessons, study materials, practice tests, revision notes, etc. Thus, we empower students to excel academically and gain confidence in their abilities.
Section and Mid-Point Formula Exercise Ex. 13(A)
Solution 1
(i) Let the co-ordinates of the point P be (x, y).
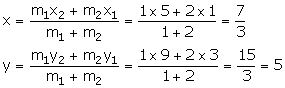
Thus,
the co-ordinates of point P are![]() .
.
(ii) Let the co-ordinates of the point P be (x, y).
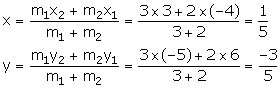
Thus,
the co-ordinates of point P are![]() .
.
Solution 2
Let the line joining points A (2, -3) and B (5, 6) be divided by point P (x, 0) in the ratio k: 1.
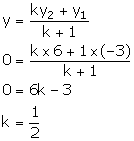
Thus, the required ratio is 1: 2.
Solution 3
Let the line joining points A (2, -4) and B (-3, 6) be divided by point P (0, y) in the ratio k: 1.
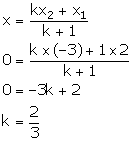
Thus, the required ratio is 2: 3.
Solution 4
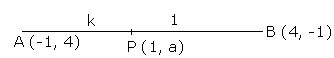
Let the point P (1, a) divides the line segment AB in the ratio k: 1.
Using section formula, we have:

Solution 5
Let the point P (a, 6) divides the line segment joining A (-4, 3) and B (2, 8) in the ratio k: 1.
Using section formula, we have:

Solution 6
Let the point P (x, 0) on x-axis divides the line segment joining A (4, 3) and B (2, -6) in the ratio k: 1.
Using section formula, we have:
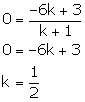
Thus, the required ratio is 1: 2.
Also, we have:
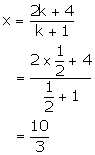
Thus,
the required co-ordinates of the point of intersection are ![]() .
.
Solution 7
![]()
Let S (0, y) be the point on y-axis which divides the line segment PQ in the ratio k: 1.
Using section formula, we have:
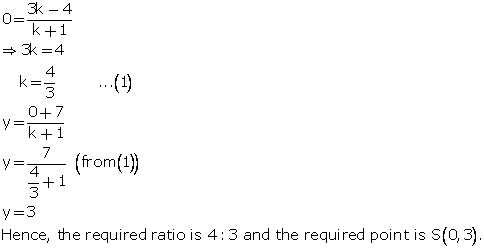
Solution 8

Point A divides PO in the ratio 1: 4.
Co-ordinates of point A are:
![]()
Point B divides PO in the ratio 2: 3.
Co-ordinates of point B are:
![]()
Point C divides PO in the ratio 3: 2.
Co-ordinates of point C are:
![]()
Point D divides PO in the ratio 4: 1.
Co-ordinates of point D are:
![]()
Solution 9
Let the co-ordinates of point P are (x, y).
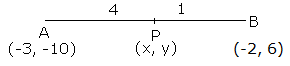
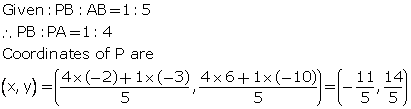
Solution 10
5AP = 2BP
![]()
The co-ordinates of the point P are
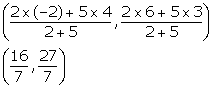
Solution 11
The co-ordinates of every point on the line x = 2 will be of the type (2, y).
Using section formula, we have:

Thus, the required ratio is 5: 3.
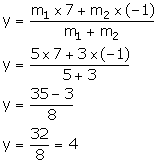
Thus, the required co-ordinates of the point of intersection are (2, 4).
Solution 12
The co-ordinates of every point on the line y = 2 will be of the type (x, 2).
Using section formula, we have:
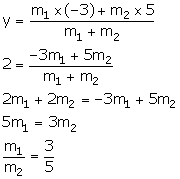
Thus, the required ratio is 3: 5.
Solution 13
Point A lies on x-axis. So, let the co-ordinates of A be (x, 0).
Point B lies on y-axis. So, let the co-ordinates of B be (0, y).
P divides AB in the ratio 2: 5.
We have:
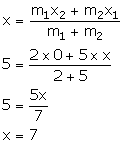
Thus, the co-ordinates of point A are (7, 0).
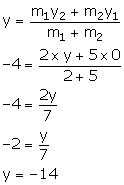
Thus, the co-ordinates of point B are (0, -14).
Solution 14
Let P and Q be the points of trisection of the line segment joining the points A(-3, 0) and B(6, 6).
So, AP = PQ = QB
We have AP: PB = 1: 2
Co-ordinates of the point P are

We have AQ: QB = 2: 1
Co-ordinates of the point Q are

Solution 15
Let P and Q be the points of trisection of the line segment joining the points A (-5, 8) and B (10, -4).
So, AP = PQ = QB
We have AP: PB = 1: 2
Co-ordinates of the point P are
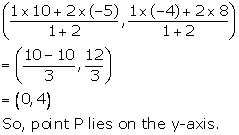
We have AQ: QB = 2: 1
Co-ordinates of the point Q are

So, point Q lies on the x-axis.
Hence, the line segment joining the given points A and B is trisected by the co-ordinate axes.
Solution 16
Let A and B be the point of trisection of the line segment joining the points P (2, 1) and Q (5, -8).
So, PA = AB = BQ
We have PA: AQ = 1: 2
Co-ordinates of the point A are
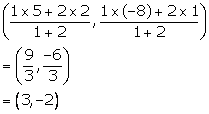
Hence, A (3, -2) is a point of trisection of PQ.
We have PB: BQ = 2: 1
Co-ordinates of the point B are

Solution 17
(i) A (-4,3) and B (8, -6)
AB =![]()

(ii) Let P be the point on the x-axis which divides AB in the ratio k : 1.
Therefore, y-co-ordinate of P = 0.
![]()
![]() = 0
= 0
![]() -6k + 3 = 0
-6k + 3 = 0
![]() k =
k =![]()
Hence, required ratio is 1: 2.
Solution 18
Since, point L lies on y-axis, its abscissa is 0.
Let the co-ordinates of point L be (0, y). Let L divides MN in the ratio k: 1.
Using section formula, we have:

Thus, the required ratio is 5: 3.

Solution 19
(i) Co-ordinates of P are

Co-ordinates of Q are

(ii) Using distance formula, we have:
BC
= ![]()
PQ
= ![]()
Hence,
PQ = ![]() BC.
BC.
Solution 20
BP: PC = 2: 3
Co-ordinates of P are
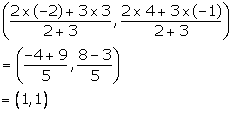
Using distance formula, we have:
![]()
Solution 21
Since, point K lies on x-axis, its ordinate is 0.
Let the point K (x, 0) divides AB in the ratio k: 1.
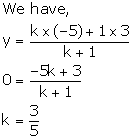
Thus, K divides AB in the ratio 3: 5.
Also, we have:
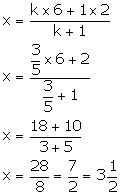
Thus,
the co-ordinates of the point K are ![]() .
.
Solution 22
Since, point K lies on y-axis, its abscissa is 0.
Let the point K (0, y) divides AB in the ratio k: 1.
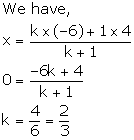
Thus, K divides AB in the ratio 2: 3.
Also, we have:
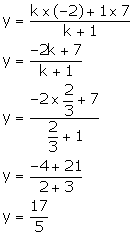
Thus,
the co-ordinates of the point K are ![]() .
.
Solution 23
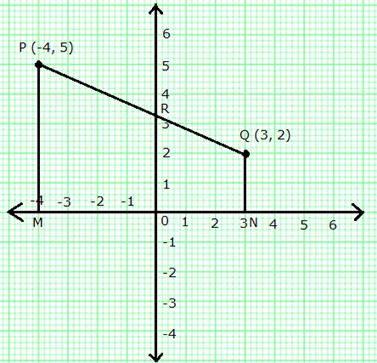
(i) Let point R (0, y) divides PQ in the ratio k: 1.
We have:
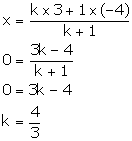
Thus, PR: RQ = 4: 3
(ii) Also, we have:
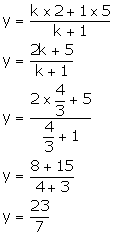
Thus,
the co-ordinates of point R are ![]() .
.
(iii) Area of quadrilateral PMNQ
=
![]() (PM + QN)
(PM + QN) ![]() MN
MN
=
![]() (5 + 2)
(5 + 2) ![]() 7
7
=
![]() 7
7 ![]() 7
7
= 24.5 sq units
Solution 24
Given, A lies on x-axis and B lies on y-axis.
Let the co-ordinates of A and B be (x, 0) and (0, y) respectively.
Given, P is the point (-4, 2) and AP: PB = 1: 2.
Using section formula, we have:
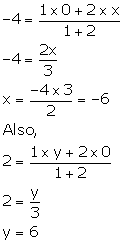
Thus, the co-ordinates of points A and B are (-6, 0) and (0, 6) respectively.
Solution 25
(i)

(ii)
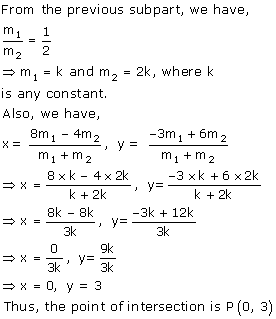
(iii)

Solution 26
Take (x1 , y1) = (-3, 3a + 1) ; (x2 , y2) = (5, 8a) and
(x, y) = (-b, 9a - 2)
Here m1 = 3 and m2 =1
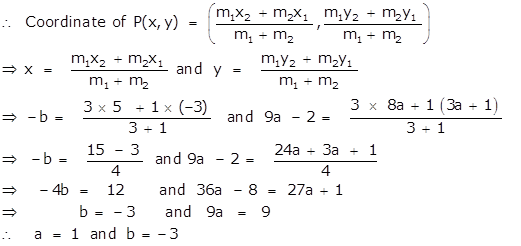
Section and Mid-Point Formula Exercise Ex. 13(B)
Solution 1
(i) A (-6, 7) and B (3, 5)
Mid-point of AB = ![]()
(ii) A (5, -3) and B (-1, 7)
Mid-point of AB = ![]()
Solution 2
Mid-point of AB = (2, 3)
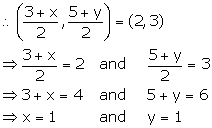
Solution 3
Given, L is the mid-point of AB and M is the mid-point of AC.
Co-ordinates of L are
![]()
Co-ordinates of M are
![]()
Using distance formula, we have:

Solution 4
(i) Let the co-ordinates of A be (x, y).
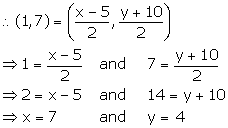
Hence, the co-ordinates of A are (7, 4).
(ii) Let the co-ordinates of B be (x, y).
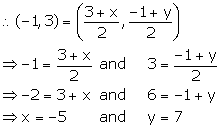
Hence, the co-ordinates of B are (-5, 7).
Solution 5
Point A lies on y-axis, so let its co-ordinates be (0, y).
Point B lies on x-axis, so let its co-ordinates be (x, 0).
P (-3, 2) is the mid-point of line segment AB.
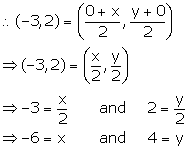
Thus, the co-ordinates of points A and B are (0, 4) and (-6, 0) respectively.
Solution 6
Point A lies on x-axis, so let its co-ordinates be (x, 0).
Point B lies on y-axis, so let its co-ordinates be (0, y).
P (4, 2) is mid-point of line segment AB.
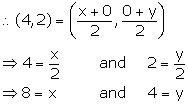
Hence, the co-ordinates of points A and B are (8, 0) and (0, 4) respectively.
Solution 7
Let A (-5, 2), B (3, -6) and C (7, 4) be the vertices of the given triangle.
Let AD be the median through A, BE be the median through B and CF be the median through C.

We know that median of a triangle bisects the opposite side.
Co-ordinates of point F are
![]()
Co-ordinates of point D are
![]()
Co-ordinates of point E are
![]()
The median of the triangle through the vertex B(3, -6) is BE
Using distance formula,
![]()
Solution 8
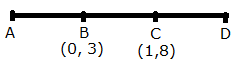
Given, AB = BC = CD
So, B is the mid-point of AC. Let the co-ordinates of point A be (x, y).
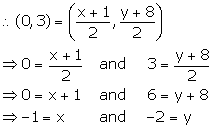
Thus, the co-ordinates of point A are (-1, -2).
Also, C is the mid-point of BD. Let the co-ordinates of point D be (p, q).

Thus, the co-ordinates of point D are (2, 13).
Solution 9
We know that the centre of the circle is the mid-point of diameter.
Let the required co-ordinates of the other end of diameter be (x, y).
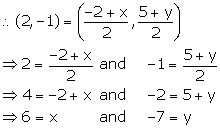
Thus, the required co-ordinates are (6, -7).
Solution 10
Co-ordinates of the mid-point of AC are
![]()
Co-ordinates of the mid-point of BD are
![]()
Since, mid-point of AC = mid-point of BD
Hence, ABCD is a parallelogram.
Solution 11
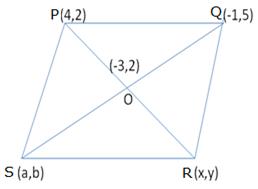
Let the coordinates of R and S be (x,y) and (a,b) respectively.
Mid-point of PR is O.
![]() O(-3,2) =
O(-3,2) = ![]()
![]()
-6 = 4 + x, 4 = 2 + y
x = -10 , y = 2
Hence, R = (-10,2)
Similarly, the mid-point of SQ is O.
![]()
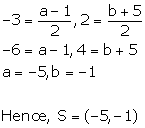
Thus, the coordinates of the point R and S are (-10, 2) and (-5, -1).
Solution 12
Let the co-ordinates of vertex C be (x, y).
ABCD is a parallelogram.
![]() Mid-point of AC = Mid-point of BD
Mid-point of AC = Mid-point of BD

Thus, the co-ordinates of vertex C are (5, 8).
Solution 13
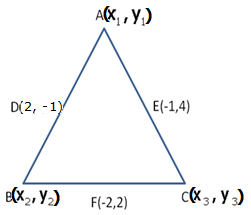
Let A(x1,y1), B![]() and C
and C![]() be the co-ordinates of the vertices of
be the co-ordinates of the vertices of ![]() ABC.
ABC.
Midpoint of AB, i.e. D
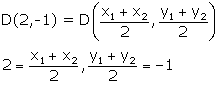
![]()
![]()
Similarly,
![]()
![]()
![]()
![]()
Adding (1), (3) and (5), we get,
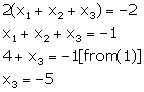
From (3)
![]()
From (5)
![]()
Adding (2), (4) and (6), we get,
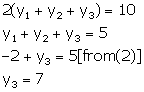
From (4)
![]()
From (6)
![]()
Thus, the co-ordinates of the vertices of ![]() ABC are (3, 1), (1, -3) and (-5, 7).
ABC are (3, 1), (1, -3) and (-5, 7).
Solution 14
Given, AB = BC, i.e., B is the mid-point of AC.

Solution 15
Given, PR = 2QR
Now, Q lies between P and R, so, PR = PQ + QR
![]() PQ + QR = 2QR
PQ + QR = 2QR
![]() PQ = QR
PQ = QR
![]() Q is the
mid-point of PR.
Q is the
mid-point of PR.
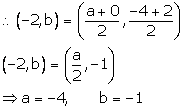
Solution 16
Co-ordinates of the centroid of triangle ABC are
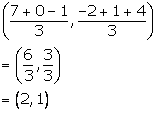
Solution 17
Let G be the centroid of DPQR whose coordinates are (2, -5) and let (x,y) be the coordinates of vertex P.
Coordinates of G are,

6 = x + 5, -15 = y + 13
x = 1, y = -28
Coordinates of vertex P are (1, -28)
Solution 18
Given, centroid of triangle ABC is the origin.

Section and Mid-Point Formula Exercise Ex. 13(C)
Solution 1
Given, BP: PC = 3: 2
Using section formula, the co-ordinates of point P are

Using distance formula, we have:
![]()
Solution 2
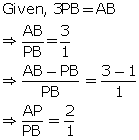
Using section formula,
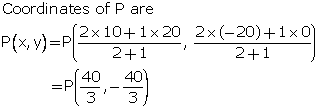
Given, AB = 6AQ

Using section formula,
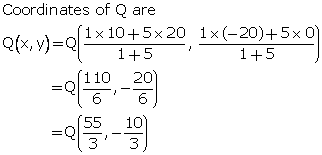
Solution 3
Given that, point P lies on AB such that AP: PB = 3: 5.
The co-ordinates of point P are

Also, given that, point Q lies on AC such that AQ: QC = 3: 5.
The co-ordinates of point Q are

Using distance formula,
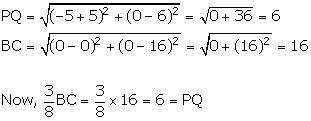
Hence, proved.
Solution 4
Let P and Q be the points of trisection of the line segment joining A (6, -9) and B (0, 0).
P divides AB in the ratio 1: 2. Therefore, the co-ordinates of point P are
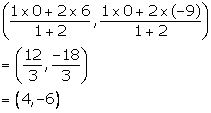
Q divides AB in the ratio 2: 1. Therefore, the co-ordinates of point Q are

Thus, the required points are (4, -6) and (2, -3).
Solution 5
Since, the line segment AB intersects the y-axis at point P, let the co-ordinates of point P be (0, y).
P divides AB in the ratio 1: 3.

Thus,
the value of a is 3 and the co-ordinates of point P are![]() .
.
Solution 6
Let the line segment AB intersects the x-axis at point P (x, 0) in the ratio k: 1.
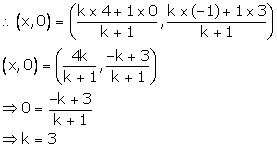
Thus, the required ratio in which P divides AB is 3: 1.
Also, we have:
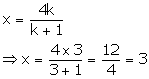
Thus, the co-ordinates of point P are (3, 0).
Solution 7
Since, point A lies on x-axis, let the co-ordinates of point A be (x, 0).
Since, point B lies on y-axis, let the co-ordinates of point B be (0, y).
Given, mid-point of AB is C (4, -3).
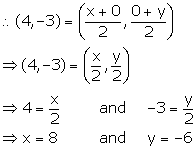
Thus, the co-ordinates of point A are (8, 0) and the co-ordinates of point B are (0, -6).
Solution 8
![]()

Solution 9
Co- ordinates of the centroid of triangle ABC are
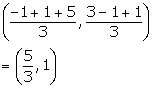
Solution 10
It is given that the mid-point of the line-segment joining (4a, 2b - 3) and (-4, 3b) is (2, -2a).
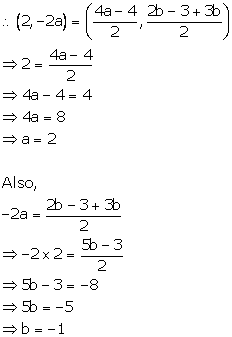
Solution 11
Mid-point of (2a, 4) and (-2, 2b) is (1, 2a + 1), therefore using mid-point formula, we have:
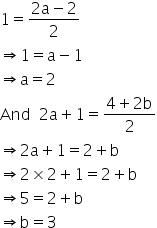
Solution 12
(i) Co-ordinates of point P are

(ii)
OP = ![]()
(iii) Let AB be divided by the point P (0, y) lying on y-axis in the ratio k: 1.

Thus, the ratio in which the y-axis divide the line AB is 4: 17.
Solution 13
We have:
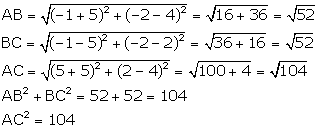
![]() AB = BC and
AB = BC and ![]()
![]() ABC is an isosceles right-angled triangle.
ABC is an isosceles right-angled triangle.
Let the coordinates of D be (x, y).
If ABCD is a square, then,
Mid-point of AC = Mid-point of BD
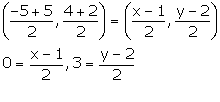
x = 1, y = 8
Thus, the co-ordinates of point D are (1, 8).
Solution 14
Given, M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1).
The co-ordinates of point M are

Also, given that, R (2, 2) divides the line segment joining M and the origin in the ratio p: q.

Thus, the ratio p: q is 1: 2.
Solution 15

Solution 16

Solution 17
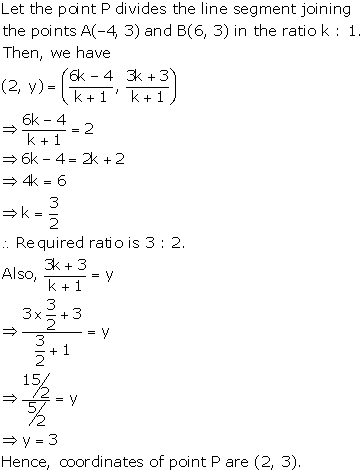
Solution 18
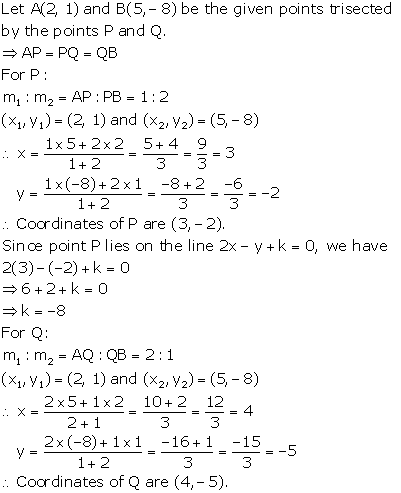
Solution 19
Let A' = (x, y) be the image of the point A(5, -3), under reflection in the point P(-1, 3).
⇒ P(-1, 3) is the mid - point of the line segment AA'.
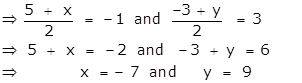
Therefore the image of the point A(5, -3), under reflection in the point P(-1, 3) is A'(-7, 9).
Solution 20

Solution 21

Solution 22
Centroid
of a △ABC
=![]() …… (i)
…… (i)
G(3, 4) is a centroid of △ABC ….. given
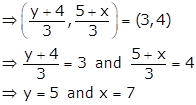
Therefore, the coordinates of B and C are (5, 4) and (1, 7) respectively.
Length of the side BC