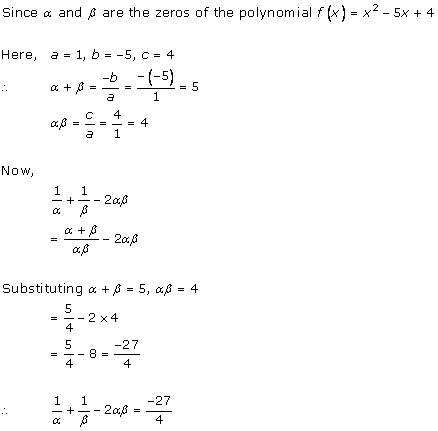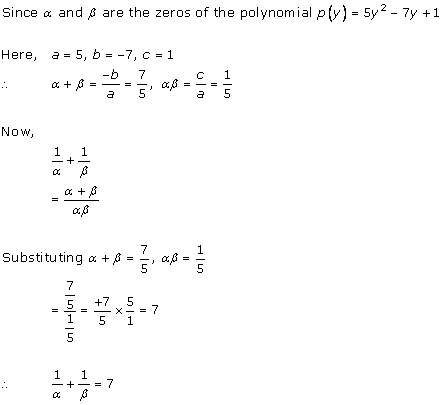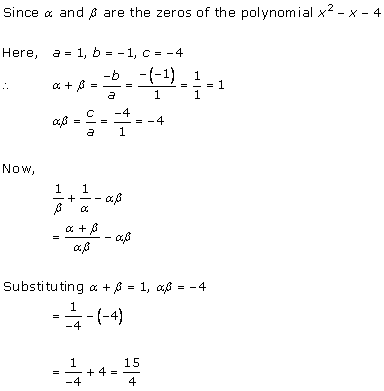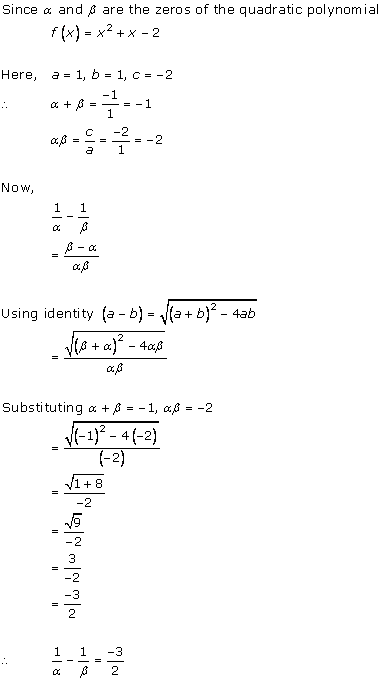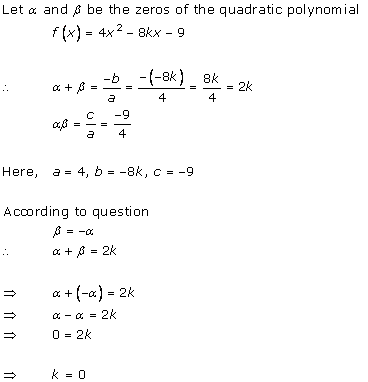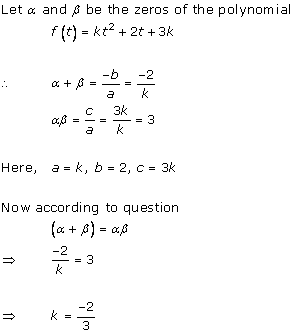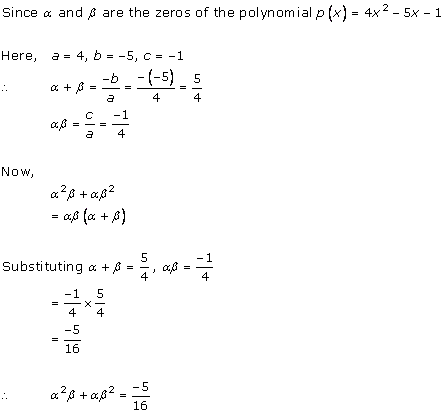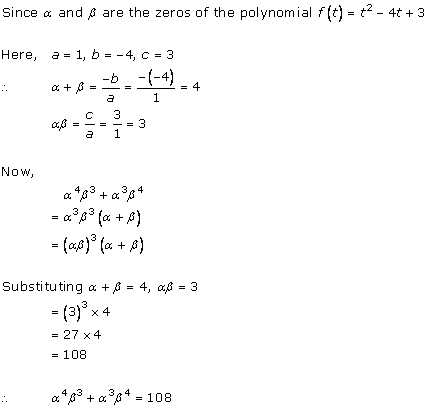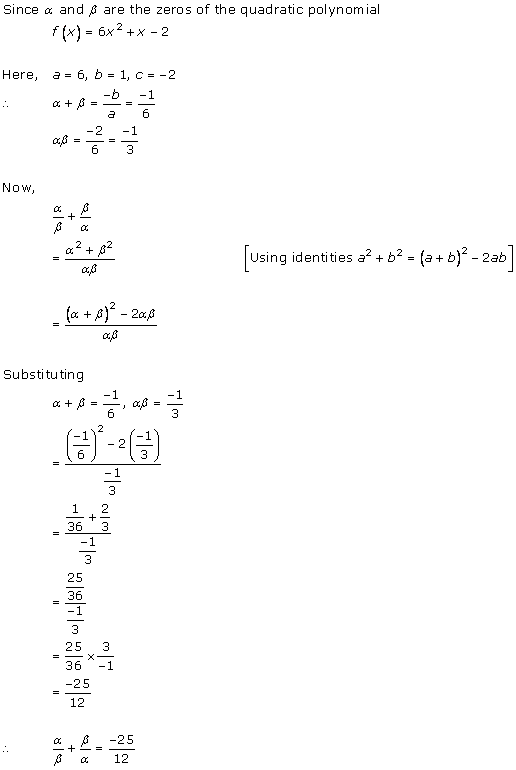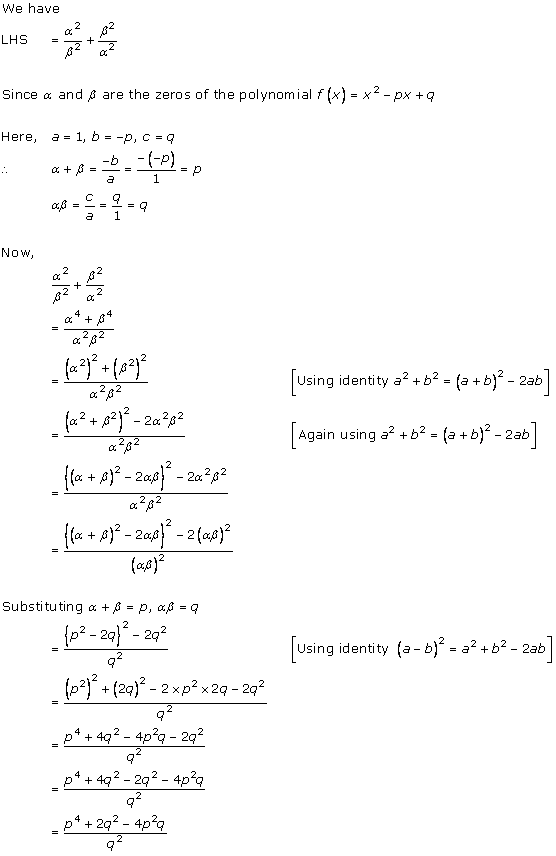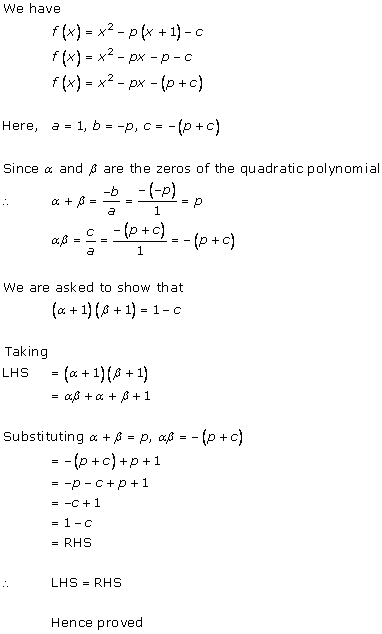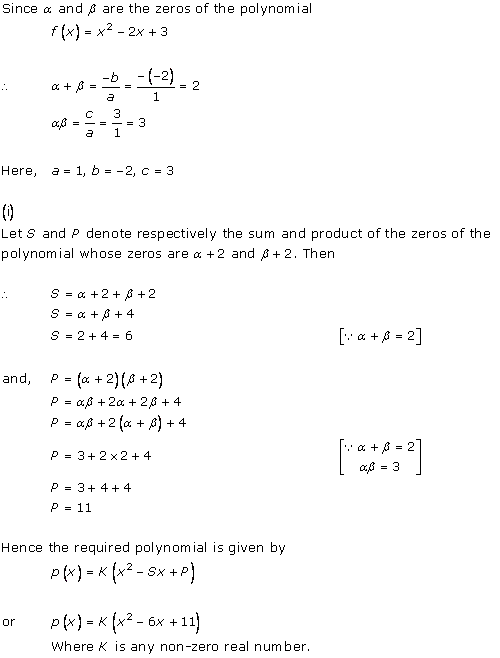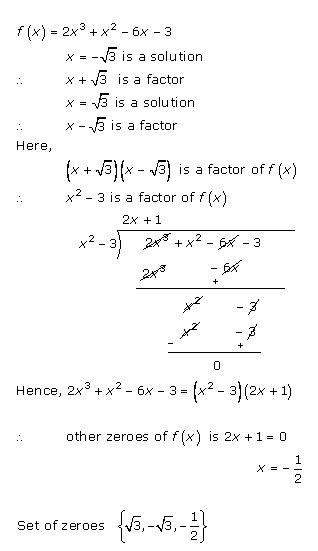Class 10 RD SHARMA Solutions Maths Chapter 2 - Polynomials
Polynomials Exercise Ex. 2.1
Solution 1(i)
x2 - 2x - 8 = x2 - 4x + 2x - 8 = x(x - 4) + 2(x - 4) = (x - 4)(x + 2)
The zeroes of the quadratic equation are 4 and -2.
Let ∝ = 4 and β = -2 Consider f(x) = x2 - 2x - 8
Sum of the zeroes = 
…(i)
Also, ∝ + β = 4 - 2 = 2 …(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = -8 …(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship between the zeroes and their coefficients is verified.
Solution 1(ii)
4s2
- 4s + 1
= 4s2 - 2s - 2s + 1
= 2s(2s - 1) - (2s - 1)
= (2s - 1)(2s - 1)
The zeroes of the quadratic equation are 
and .
Let ∝ = and β =
Consider4s2 - 4s + 1
Sum of the zeroes = 
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(iii)
h (t) = t2 - 15 = (t + √15)(t - √15)
The zeroes of the quadratic equation are
and 
.
Let ∝ = and β =
Considert2 - 15 = t2 - 0t - 15
Sum of the zeroes = 
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(iv)
f(s) = 0
6x2 - 3 - 7x =0 6x2 - 9x + 2x - 3 = 0
3x (2x - 3) + (2x - 3) = 0
(3x + 1) (2x - 3) = 0
The zeroes of a quadratic equation are 
and
.
Let ∝ = and β =
Consider6x2 - 7x - 3 = 0
Sum of the zeroes = 
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(v)
The zeroes of a quadratic equation are 
and 
.
Let ∝ = and β =
Consider
Sum of the zeroes = 
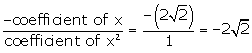…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(vi)
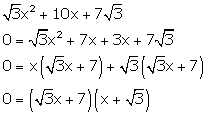The zeroes of a quadratic equation are 
and 
.
Let ∝ = and β =
Consider
Sum of the zeroes = 
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(vii)
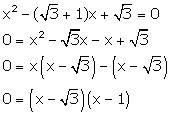The zeroes of a quadratic equation are 
and 1.
Let ∝ = and β = 1
Consider
Sum of the zeroes =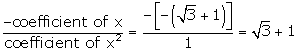
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(viii)
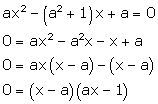The zeroes of a quadratic equation are a and
.
Let ∝ = a and β
=
Consider
Sum of the zeroes =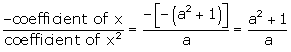
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(ix)
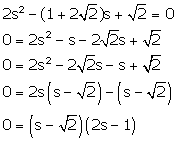The zeroes of a quadratic equation are and .
Let ∝ = and β =
Consider
Sum of the zeroes =
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(x)
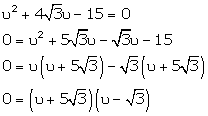The zeroes of a quadratic equation are 
and .
Let ∝ = and β =
Consider
=0
Sum of the zeroes =
…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(xi)
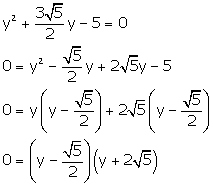The zeroes of a quadratic equation are 
and
.
Let ∝ = and β =
Consider
=0
Sum of the zeroes =
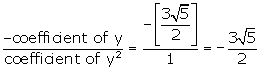…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes = 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 1(xii)
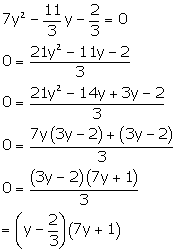The zeroes of a quadratic equation are 
and
.
Let ∝ = and β =
Consider
=0
Sum of the zeroes =
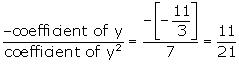…(i)
Also, ∝ + β = 
…(ii)
Product of the zeroes =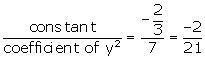 
…(iii)
Also, ∝ β = 
…(iv)
Hence, from (i), (ii), (iii) and (iv),the relationship
between the zeroes and their coefficients is verified.
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
Solution 2(iv)
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
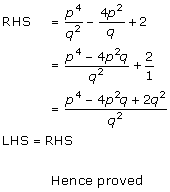
Solution 15
Solution 16
Solution 17
Solution 18
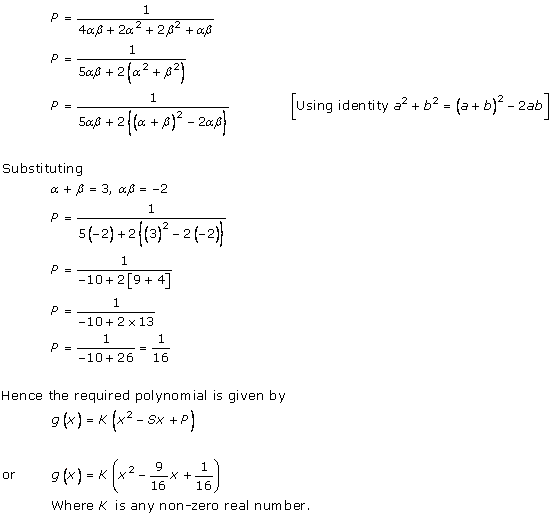
Solution 19
Solution 20
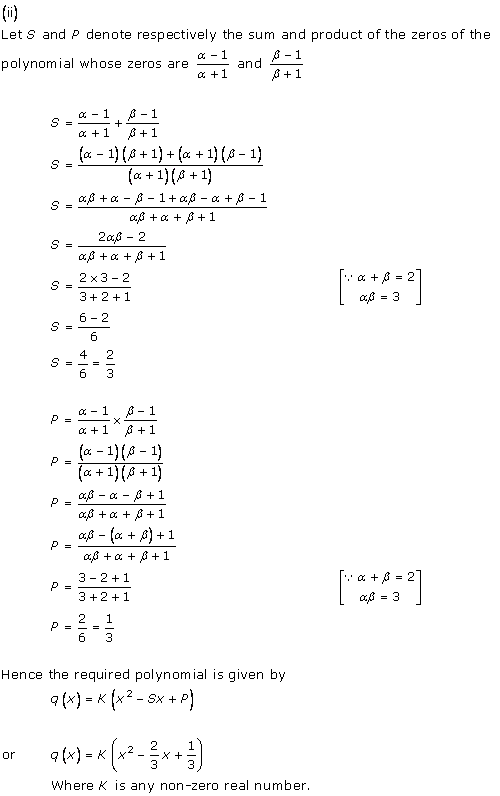
Solution 21
(i) 
(ii) 
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
Polynomials Exercise Ex. 2.2
Solution 1
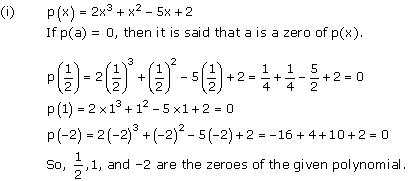
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 2, b = 1, c = -5, d = 2
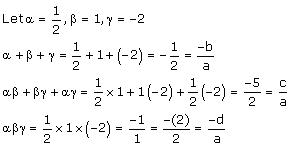
Thus, the relationship between the zeroes and the coefficients is verified.
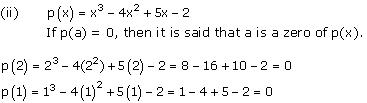
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 1, b = -4, c = 5, d = -2.
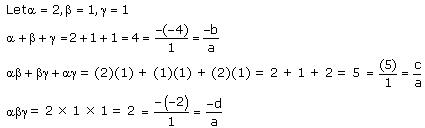
Thus, the relationship between the zeroes and the coefficients is verified.
Concept insight: The zero of a polynomial is that value of the variable which makes the polynomial 0. Remember that there are three relationships between the zeroes of a cubic polynomial and its coefficients which involve the sum of zeroes, product of all zeroes and the product of zeroes taken two at a time.
Solution 2
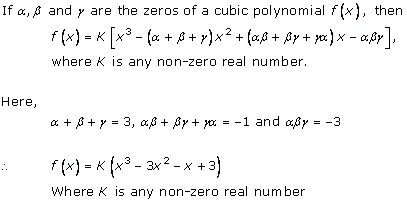
Solution 3
Let f(x) = 3x3 + 10x2 - 9x - 4
As 1 is one of the zeroes of the polynomial, so (x - 1) becomes the factor of f(x).
Dividing f(x) by (x - 1), we have
Hence, the zeroes
are 
Solution 4
Let f(x) = x3 - 3x2 - 10x + 24
As 4 is one of the zeroes of the polynomial, so (x - 4) becomes the factor of f(x).
Dividing f(x) by (x - 4), we have
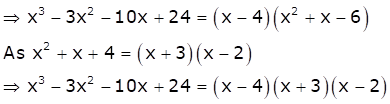
Hence, the zeroes are 4, -3 and 2.
Solution 5
Solution 6
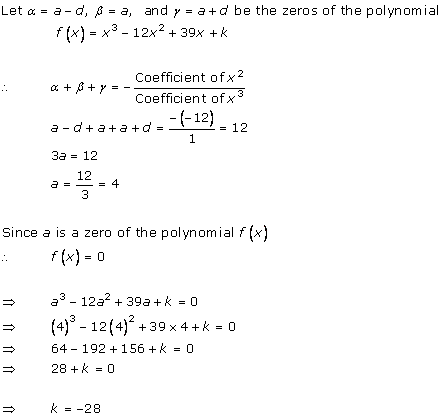
Polynomials Exercise Ex. 2.3
Solution 1 (i)
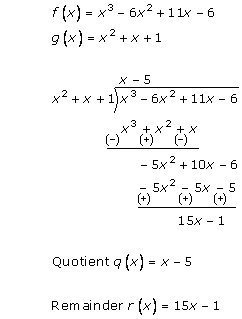
Solution 1 (ii)
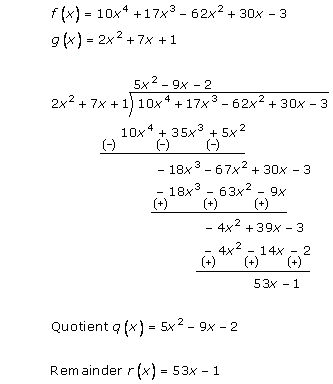
Solution 1 (iii)
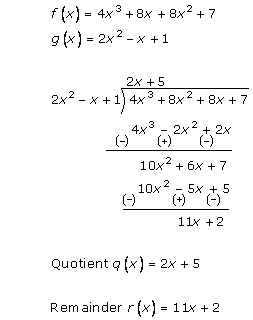
Solution 1 (iv)
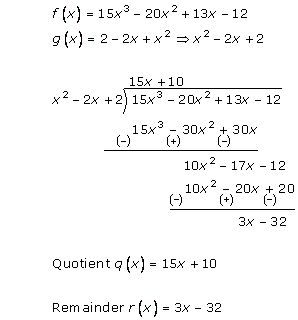
Solution 2
Solution 3
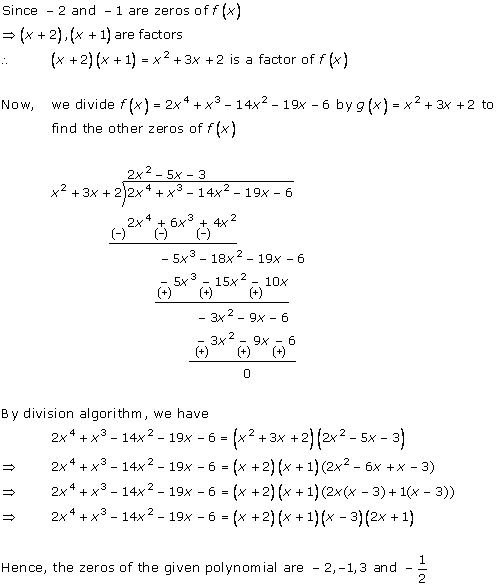
Solution 4
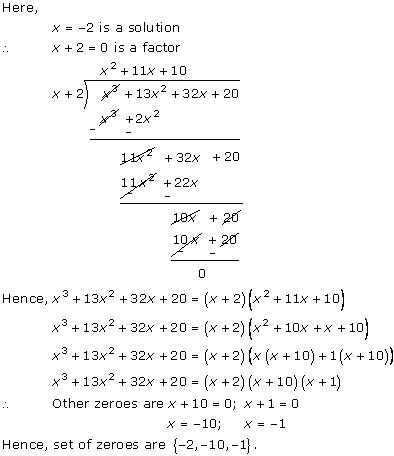
Solution 5
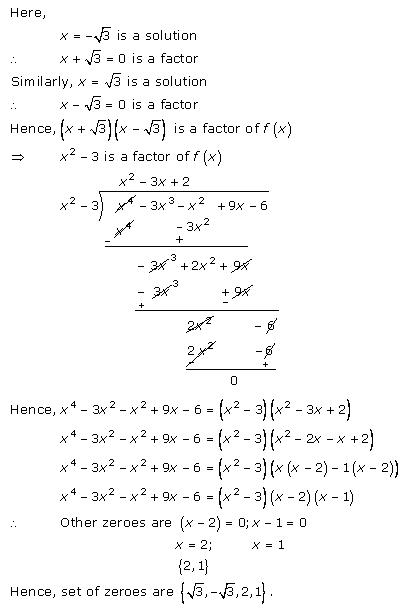
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Let f(x) = 2x4 - 9x3 + 5x2 + 3x - 1
As 
are two of the
zeroes of the polynomial, so 
becomes the factor
of f(x).
Dividing f(x) by 
we have
Hence, the other
zeros 
Solution 12
Let f(x) = 3x4 - 9x3 + x2 + 15x + k
As f(x) is completely divisible by 3x2 - 5, it becomes one of the factors of f(x).
Dividing f(x) by 3x2 - 5, we have
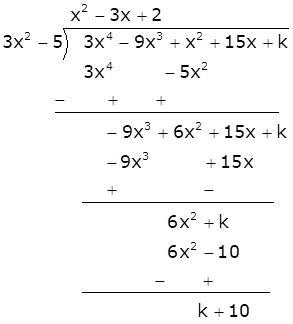
As (3x2 - 5) is one of the factors, the remainder will be 0.
Therefore, k + 10 = 0
Thus, k = -10.
Solution 13
Solution 14
Polynomials Exercise 2.61
Solution 1
Solution 2
So, the correct option is (d).
Solution 3
Polynomials Exercise 2.62
Solution 4
So, the correct option is (b).
Solution 5
Solution 6
Solution 7
Given that (α + 1) (β + 1) = 0
So, the correct option is (a).
Solution 8
We know that, if the quadratic equation ax2 + bx + c = 0 has no real zeros
then
Case 1:
a > 0, the graph of quadratic equation should not intersect x - axis
It must be of the type
Case 2 :
a < 0, the graph will not intersect x - axis and it must be of type
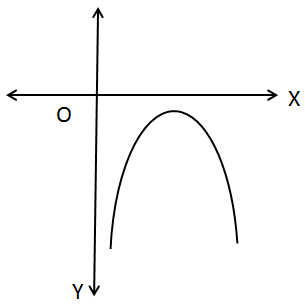
According to the question,
a + b + c < 0
This means,
f(1) = a + b + c
f(1) < 0
Hence, f(0) < 0 [as Case 2 will be applicable]
So, the correct option is (c).
Solution 9
Solution 10
Solution 11
Solution 12
Polynomials Exercise 2.63
Solution 13
So, the correct option is (b).
Solution 14
Solution 15
So, the correct option is (c).
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Polynomials Exercise 2.64
Solution 24
We know that, if α and β are roots of ax2 + bx + c = 0 then they must satisfy the equation.
According to the question, the equation is
x2 - 5x + 4 = 0
If 3 is the root of equation it must satisfy equation.
x2 - 5x + 4 = 0
but f(3) = 32 - 5(3) + 4 = -2
so, 2 has to be added in the equation.
So, the correct option is (b).
Solution 25
We know that, if α and β are roots of ax2 + bx + c = 0, then α and β must satisfy the equation.
According to the question, the equation is
x2 - 16x + 30 = 0
If 15 is a root, then it must satisfy the equation x2 - 16x + 30 = 0,
But f(15) = 152 - 16(15) + 30 = 225 - 240 + 30 = 15
and so 15 should be subtracted from the equation.
So, the correct option is (c).
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
We know that
Dividend = Divisor × quotient + remainder
Then according to question,
Required polynomial
= (-x2 + x - 1) (x - 2) + 3
= -x3 + 2x2 + x2 -2x - x + 2 + 3
= -x3 + 3x2 - 3x + 5
So, the correct option is (c).
Solution 31
Correct option: (d)
The polynomials having -2 and 5 as the zeroes can be written in the form
k(x + 2)(x - 5), where k is a constant.
Thus, number of polynomials with roots -2 and 5 are infinitely many, since k can take infinitely many values.
Solution 32
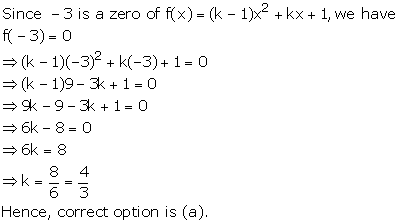
Solution 33
The zeroes of the quadratic polynomial x2 + 99x + 127 are both negative since all terms are positive.
Hence, correct option is (b).
Solution 34
Solution 35
Solution 36
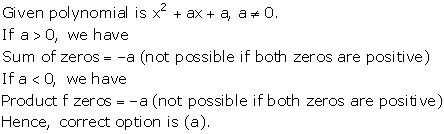
Solution 37
Polynomials Exercise 2.65
Solution 38
Solution 39
Solution 40
It is given that the zeros of the quadratic polynomial ax2 + bx + c, c ≠ 0 are equal.
⇒ Discriminant = 0
⇒ b2 - 4ac = 0
⇒ b2 = 4ac
Now, b2 can never be negative,
Hence, 4ac also can never be negative.
⇒ a and c should have same sign.
Hence, correct option is (c).
Solution 41
Solution 42
The graph of a quadratic polynomial crosses X-axis at atmost two points.
Hence, correct option is (d).
