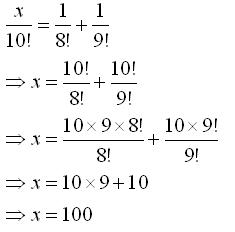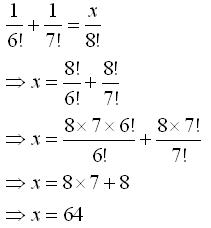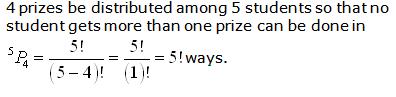Class 11-science RD SHARMA Solutions Maths Chapter 16 - Permutations
Permutations Exercise Ex. 16.1
Solution 1
Solution 2
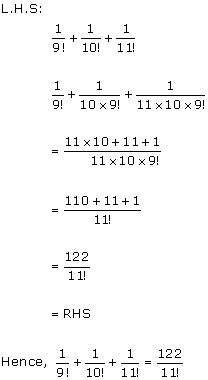
Solution 3(i)
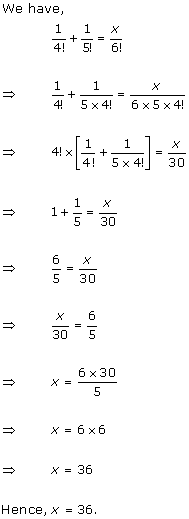
Solution 3(ii)
Solution 3(iii)
Solution 4(i)
Solution 4(ii)
Solution 4(iii)
Solution 4(iv)
Solution 5
Solution 6
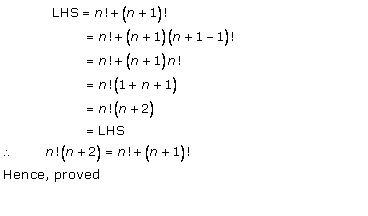
Solution 7
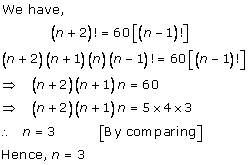
Solution 8
Solution 9
Solution 10
Solution 11(i)
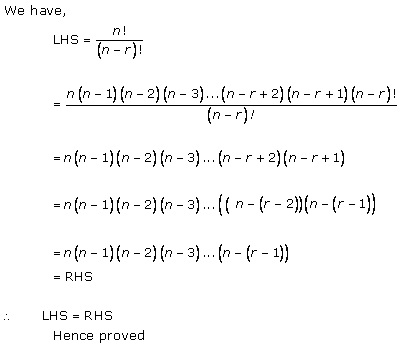
Solution 11(ii)
Solution 12
Permutations Exercise Ex. 16.2
Solution 1
Solution 2
Solution 3
Solution 4
Solution 4
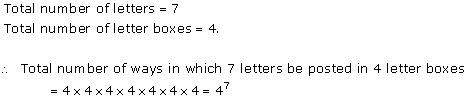
Solution 5
Solution 6
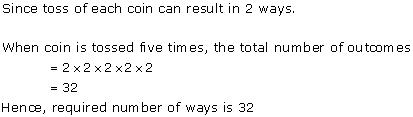
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
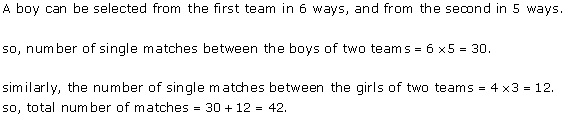
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
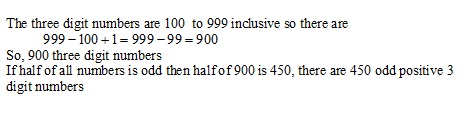
Solution 19(i)
Solution 19(ii)
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
One-digit odd number:
3 possible ways are there. These numbers are 3 or 5 or 7.
Two-digit odd number:
Tens place can be filled up by 3 ways (using any of the digit among 3, 5 and 7) and then the ones place can be filled in any of the remaining 2 digits.
So, there are 3
2 = 6 such 2-digit numbers.Three-digit odd number:
Ignore the presence of zero at ones place for some instance.
Hundreds place can be filled up in 3 ways (using any of any of the digit among 3, 5 and 7), then tens place in 3 ways by using remaining 3 digits (after using a digit, there will be three digits) and then the ones place in 2 ways.
So, there are a total of 3
3 2 = 18 numbers of 3-digit numbers which includes both odd and even numbers (ones place digit are zero). In order to get the odd numbers, it is required to ignore the even numbers i.e. numbers ending with zero. To obtain the even 3-digit numbers, ones place can be filled up in 1 way (only 0 to be filled), hundreds place in 3 ways (using any of the digit among 3, 5, 7) and then tens place in 2 ways (using remaining 2 digits after filling up hundreds place).
So, there are a total of 1
3 2 = 6 even 3-digit numbers using the digits 0, 3, 5 and 7 (repetition not allowed) So, number of three-digit odd numbers using the digits 0, 3, 5 and 7 (repetition not allowed) = 18 - 6 = 12.
Therefore, odd numbers less than 1000 can be formed by using the digits 0, 3, 5, 7 when repetition of digits is not allowed are 3 + 6 + 12 = 21.
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
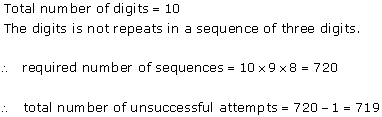
Solution 31
Solution 32
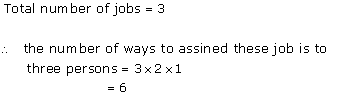
Solution 33
The given digits are 1, 2, 3 and 4. These digits can be repeated while forming the numbers. So, number of required four digit natural numbers can be found as follows.
Consider four digit natural numbers whose digit at thousandths place is 1.
Here, hundredths place can be filled in 4 ways. (Using the digits 1 or 2 or 3 or 4)
Similarly, tens place can be filled in 4 ways. (Using the digits 1 or 2 or 3 or 4)
Ones place can be filled in 4 ways. (Using the digits 1 or 2 or 3 or 4)
Number of four digit natural numbers whose digit at thousandths place is 1 = 4 
4 4 = 64
Similarly, number of four digit natural numbers whose digit at thousandths place is 2 = 4 4 4 = 64
Now, consider four digit natural numbers whose digit at thousandths place is 4:
Here, if the digit at hundredths place is 1, then tens place can be filled in 4 ways and ones place can also be filled in 4 ways.
If the digit at hundredths place is 2, then tens place can be filled in 4 ways and ones place can also be filled in 4 ways.
If the digit at hundredths place is 3 and the digit at tens place is 1, then ones place can be filled in 4 ways.
If the digit at hundredths place is 3 and the digit at tens place is 2, then ones place can be filled only in 1 way so that the number formed is not exceeding 4321.
Number of four digit natural numbers not exceeding 4321 and digit at thousandths place is 3 = 4 4 + 4 4 + 4 + 1 = 37
Thus, required number of four digit natural numbers not exceeding 4321 is 64 + 64 + 64 + 37 = 229.
Solution 34
Solution 35
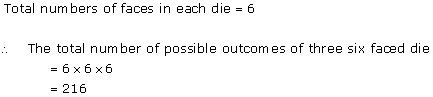
Solution 36
Solution 37
Solution 38
Solution 39
Solution 40
Solution 41
Solution 42
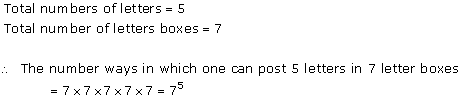
Solution 43
Solution 44
Solution 45
Solution 46
Solution 47(i)
Solution 47(ii)
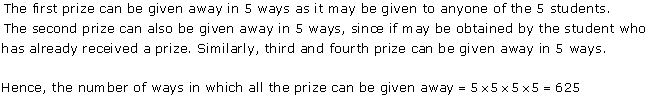
Solution 47(iii)
Solution 48
Each lamps has two possibilities either it can be switched on or off.
There are 10 lamps in the hall.
So the total numbers of possibilities are 210.
To illuminate the hall we require at least one lamp is to be switched on.
There is one possibility when all the lamps are switched off. If all the bulbs are switched off then hall will not be illuminated.
So the number of ways in which the hall can be illuminated is 210-1.
Permutations Exercise Ex. 16.3
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(i)
Solution 2
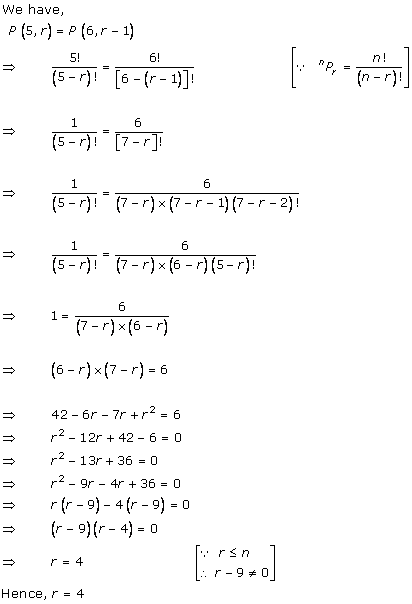
Solution 3
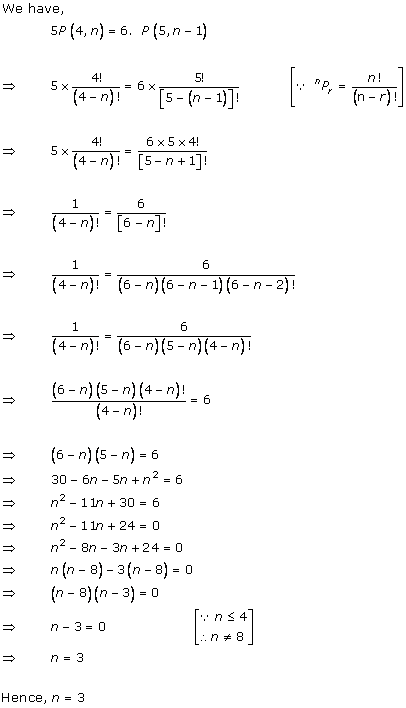
Solution 4
Solution 5
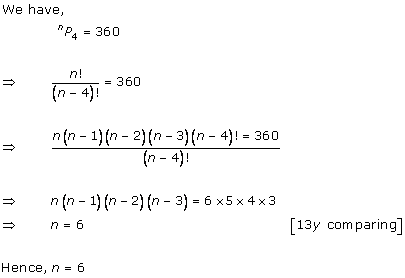
Solution 6
Solution 7
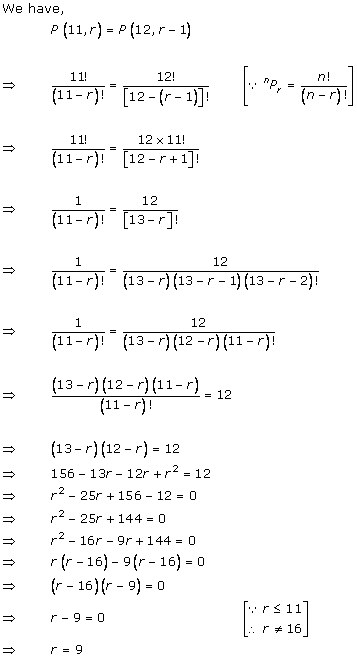
Solution 8
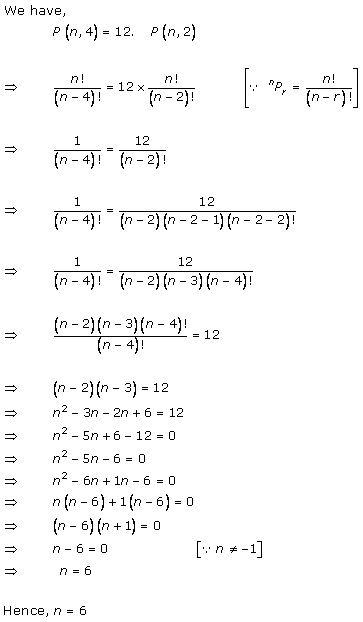
Solution 9
Solution 10
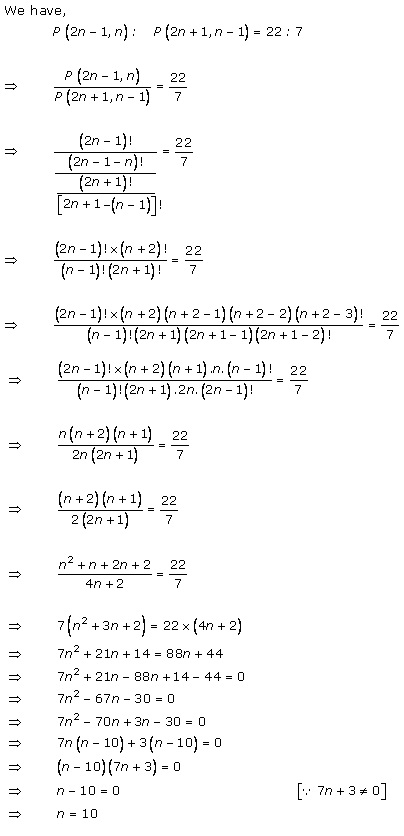
Solution 11
Solution 12
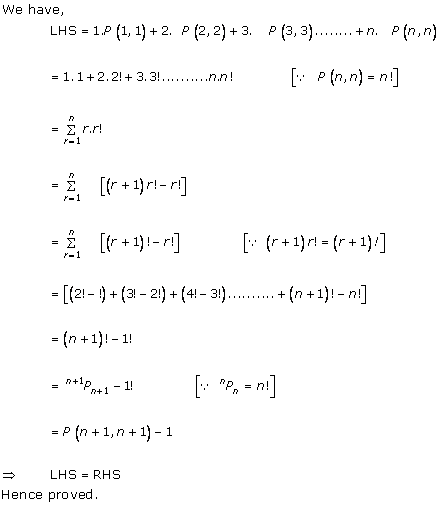
Solution 13
Solution 14
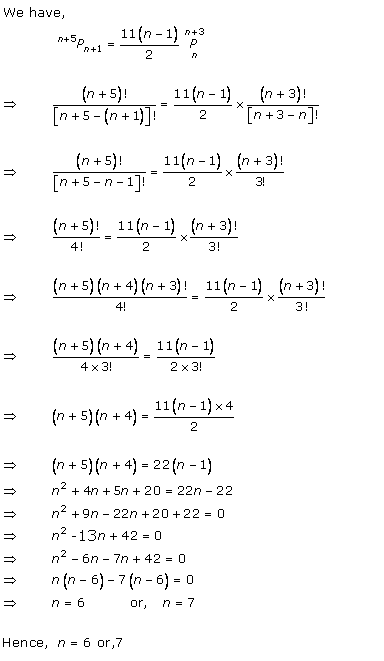
Solution 15
Solution 16
Solution 17
Solution 18
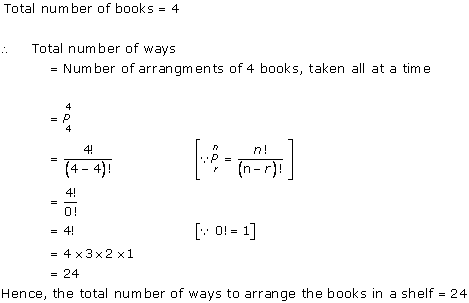
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
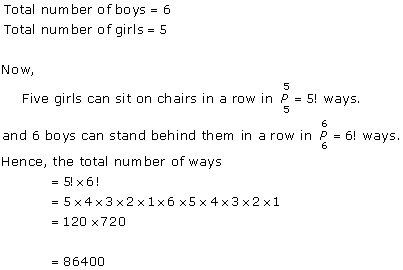
Solution 28
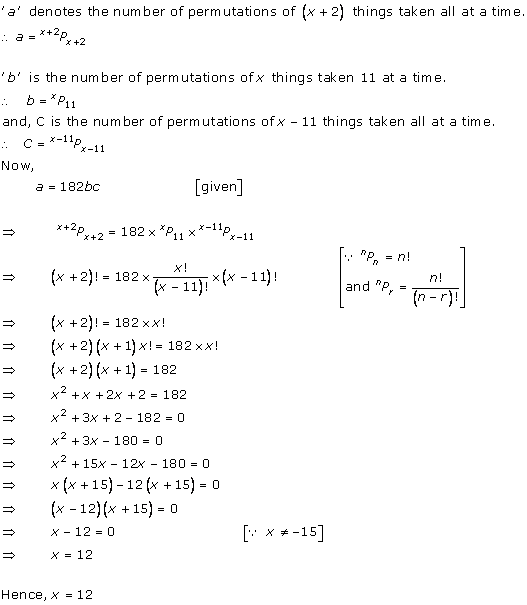
Solution 29
Solution 30
Solution 31
Solution 32
Permutations Exercise Ex. 16.4
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
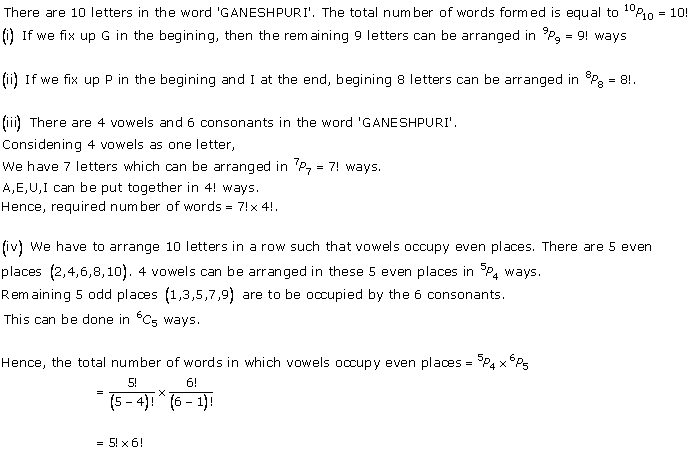
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Permutations Exercise Ex. 16.5
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
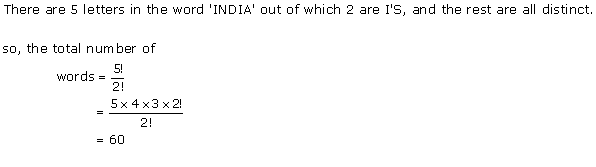
Solution 1(v)
Solution 1(vi)
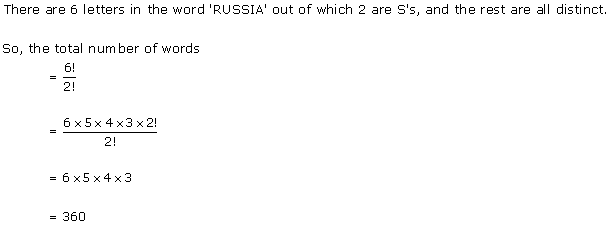
Solution 1(vii)
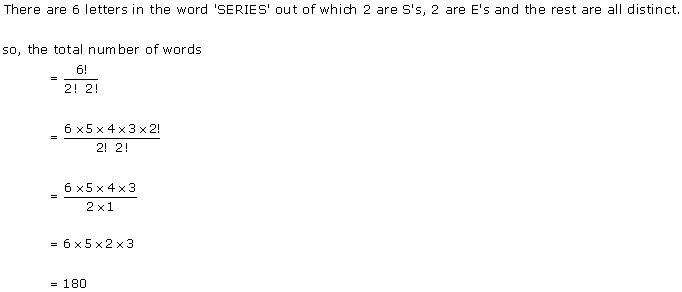
Solution 1(viii)
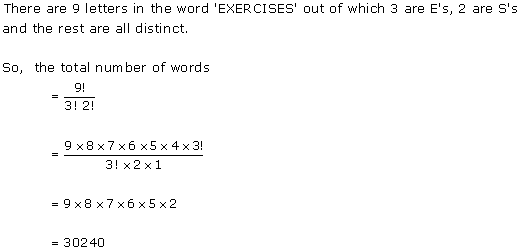
Solution 1(ix)
Solution 2
Solution 3
Solution 4
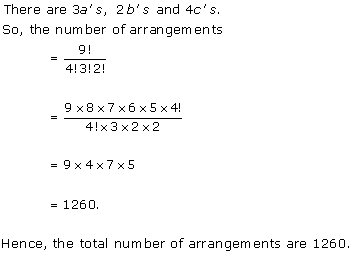
Solution 5
Solution 6
Solution 7
Solution 8
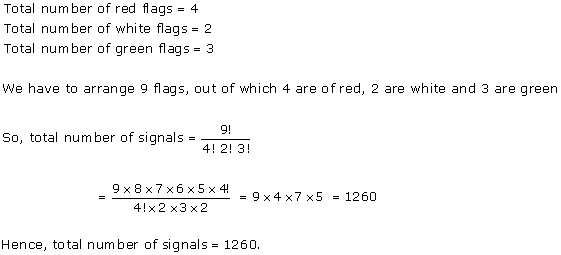
Solution 9
Solution 10
Solution 11
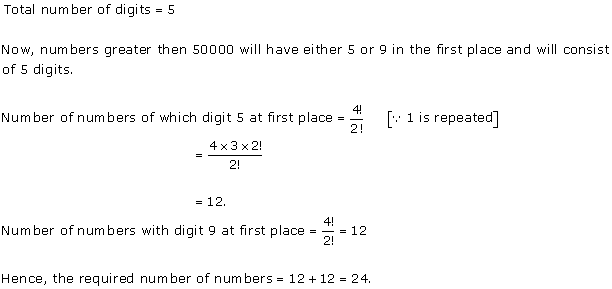
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
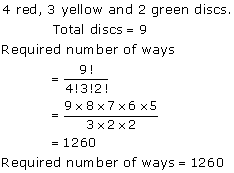
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Permutations Exercise Ex. 16VSAQ
Solution 1
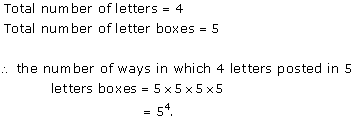
Solution 2
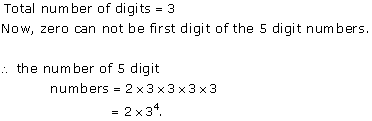
Solution 3
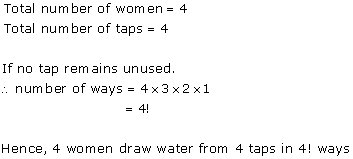
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
First we will find the least factorial term divisible by 14.
As 7!=7x6x5! is divisible by 14 leaving remainder zero.
Hence terms 7! onwards can be written as multiple of 7!.
8!=8x7!, 9!=9x8x7!... like ways 200! can also be written as multiple of 7!.
So all the terms 7! onwards are divisible by 14 leaving remainder zero.
1! + 2! + 3! + 4! + 5! + 6!
=1+2+6+24+120+720
=873
Hence remainder obtained when 1! + 2! + 3! + ….+ 200! is divided by 14 is 5.
Solution 12
Solution 13
