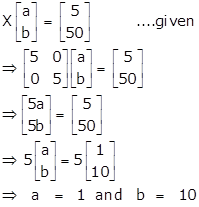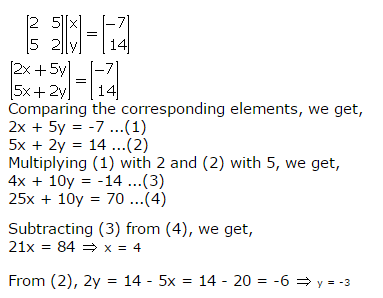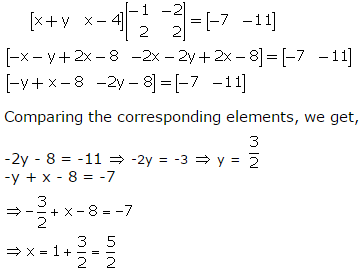Class 10 SELINA Solutions Maths Chapter 9 - Matrices
Matrices Exercise Ex. 9(A)
Solution 1
(i) False
The sum A + B is possible when the order of both the matrices A and B are same.
(ii) True
(iii) False
Transpose of a 2 
1 matrix is a 1 2 matrix.
(iv) True
(v) False
A column matrix has only one column and many rows.
Solution 2
If two matrices are equal, then their corresponding elements are also equal. Therefore, we have:
x = 3,
y + 2 = 1 
y = -1
z - 1 = 2 z = 3
Solution 3
If two matrices are equal, then their corresponding elements are also equal.
(i)
a + 5 = 2 
a = -3
-4 = b + 4 b = -8
2 = c - 1 c = 3
(ii) a= 3
a - b = -1
b = a + 1 = 4
b + c = 2
c = 2 - b = 2 - 4 = -2
Solution 4
(i) A + B =
(ii) B - A 
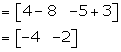
Solution 5
(i)B + C = 
(ii)A - C = 
(iii)A + B - C =
=
= 
(iv)A - B +C =
=
= 
Solution 6
(i) 
(ii) 
(iii) Addition is not possible, because both matrices are not of same order.
Solution 7
(i)
Equating the corresponding elements, we get,
3 - x = 7 and y + 2 = 2
Thus, we get, x = - 4 and y = 0.
(ii)
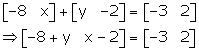
Equating the corresponding elements, we get,
-8 + y = -3 and x - 2 =2
Thus, we get, x = 4 and y = 5.
Solution 8
M =
Mt = 
(i) 
(i) 
Solution 9
We know additive inverse of a matrix is its negative.
Additive inverse of A = 
Additive inverse of B = 
Additive inverse of C = 
Solution 10
(i) X + B = C - A
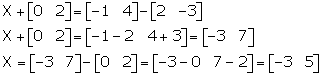
(ii) A - X = B + C
Solution 11
(i) A + X = B
X = B - A
(ii) A - X = B
X = A - B
(iii) X - B = A
X = A + B
Matrices Exercise Ex. 9(B)
Solution 1
Solution 2
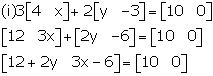
Comparing the corresponding elements, we get,
12 + 2y = 10 and 3x - 6 = 0
Simplifying, we get, y = -1 and x = 2.
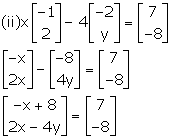
Comparing corresponding the elements, we get,
-x + 8 = 7 and 2x - 4y = -8
Simplifying, we get,
x = 1 and y = 
= 2.5
Solution 3
(i) 2A - 3B + C
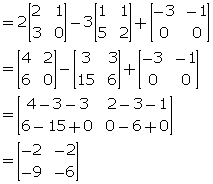
(ii) A + 2C - B
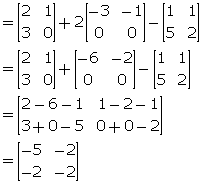
Solution 4
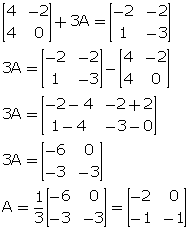
Solution 5
(i)
(ii)
C + B = 
C
= - B = 
Solution 6
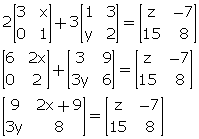
Comparing the corresponding elements, we get,
2x
+ 9 = -7 
2x = -16 x = -8
3y
= 15 y = 5
z = 9
Solution 7
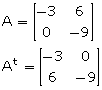
(i) 2A + 3At
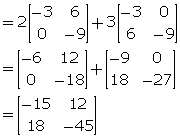
(ii) 2At - 3A
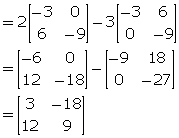
(iii)
(iv)
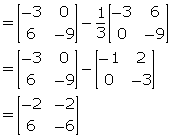
Solution 8
(i) X + 2A = B
X = B - 2A
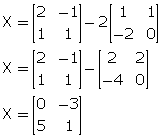
(ii) 3X + B + 2A = O
3X = -2A - B
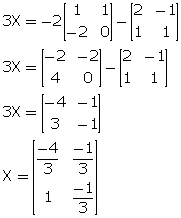
(iii) 3A - 2X = X - 2B
3A + 2B = X + 2X
3X = 3A + 2B
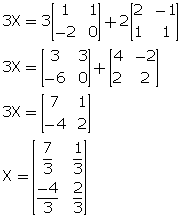
Solution 9
3M + 5N
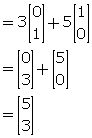
Solution 10
(i)
M - 2I = 
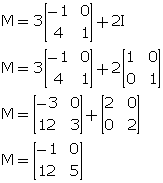
(ii)
5M + 3I = 
Solution 11
2M = 
M = 
Matrices Exercise Ex. 9(C)
Solution 1
The number of columns in the first matrix is not equal to the number of rows in the second matrix. Thus, the product is not possible.
Solution 2
Solution 3
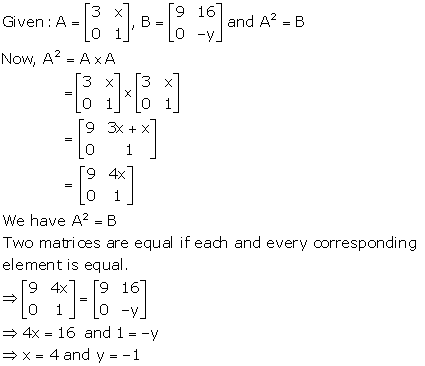
Solution 4
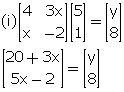
Comparing the corresponding elements, we get,
5x
- 2 = 8 
x = 2
20
+ 3x = y y = 20 + 6 =
26
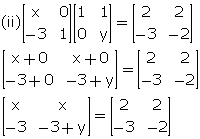
Comparing the corresponding elements, we get,
x = 2
-3
+ y = -2 y = 1
Solution 5
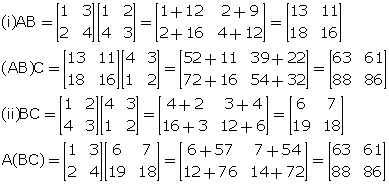
Hence, A(BC) = (AB)C.
Solution 6
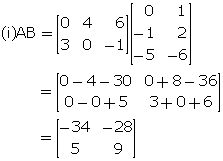
(iii) Product AA (=A2) is not possible as the number of columns of matrix A is not equal to its number of rows.
Solution 7
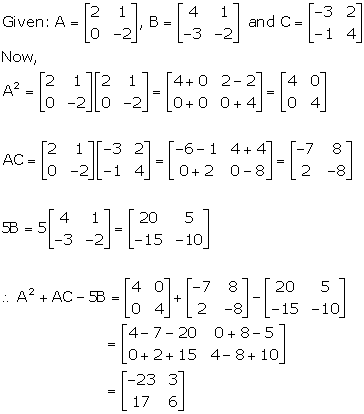
Solution 8
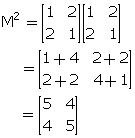
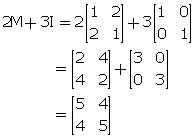
Hence, M2 = 2M + 3I.
Solution 9
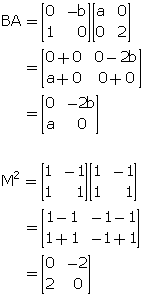
Given, BA = M2
Comparing the corresponding elements, we get,
a = 2 and -2b = -2 
b = 1
Solution 10
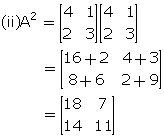
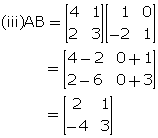
Solution 11
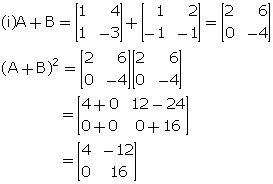
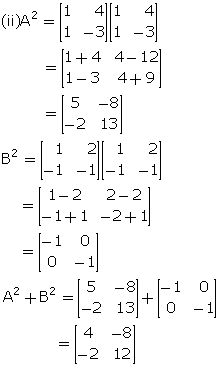
(iii)
Clearly, (A + B)2 
A2
+ B2
Solution 12
B2
= B + 
A
A = B2
- B
A = 2(B2 - B)
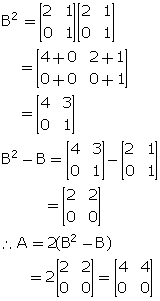
Solution 13
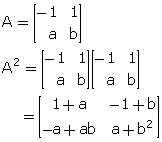
It is given that A2 = I.
Comparing the corresponding elements, we get,
1 + a = 1
Therefore, a = 0
-1 + b = 0
Therfore, b = 1
Solution 14
Solution 15
Solution 16(i)
Solution 16(ii)
Solution 16(iii)
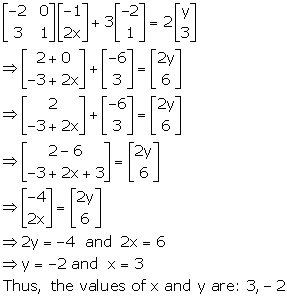
Solution 17
We know, the product of two matrices is defined only when the number of columns of first matrix is equal to the number of rows of the second matrix.
(i) Let the order of matrix M be a x b.
Clearly, the order of matrix M is 1 x 2.
Comparing the corresponding elements, we get,
a = 1 and a + 2b = 2 
2b = 2 - 1 = 1 b = 
(ii) Let the order of matrix M be a x b.
Clearly, the order of matrix M is 2 x 1.
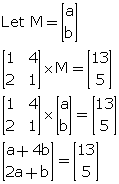
Comparing the corresponding elements, we get,
a + 4b = 13 ....(1)
2a + b = 5 ....(2)
Multiplying (2) by 4, we get,
8a + 4b = 20 ....(3)
Subtracting (1) from (3), we get,
7a = 7 a = 1
From (2), we get,
b = 5 - 2a = 5 - 2 = 3
Solution 18
Solution 19
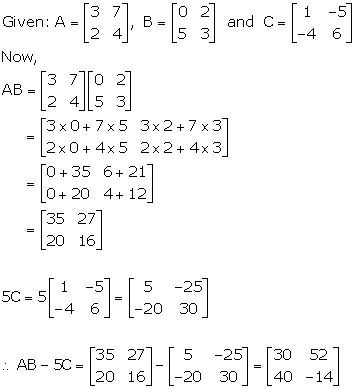
Solution 20
AB = BA = B
We know that I × B = B × I = B, where I is the identity matrix.
Hence, A is an identity matrix.
Solution 21
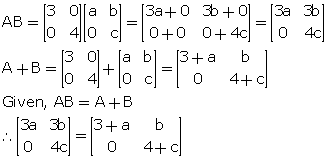
Comparing the corresponding elements, we get,
3a = 3 + a
2a = 3
a = 
3b = b 
b = 0
4c = 4 + c 3c = 4 c = 
Solution 22
Clearly, it can be said that:
(P + Q) (P - Q) = P2 - Q2 not true for matrix algebra.
Solution 23
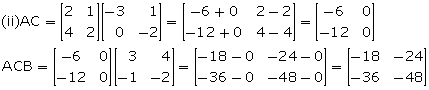
Hence, ABC ≠ ACB.
Solution 24
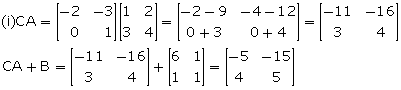
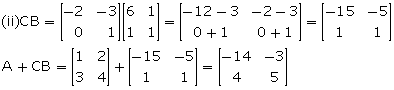
Thus, CA + B 
A + CB
Solution 25
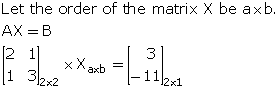
Clearly, the order of matrix X is 2 x 1.
Comparing the two matrices, we get,
2x + y = 3 … (1)
x + 3y = -11 … (2)
Multiplying (1) with 3, we get,
6x + 3y = 9 … (3)
Subtracting (2) from (3), we get,
5x = 20
x = 4
From (1), we have:
y = 3 - 2x = 3 - 8 = -5
Solution 26
Solution 27
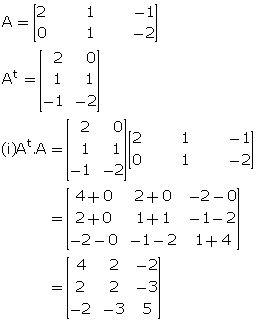
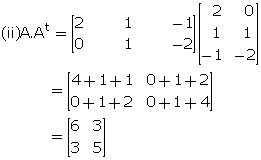
Solution 28
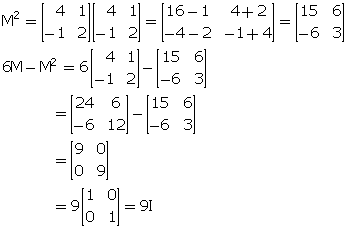
Hence, proved.
Solution 29
Comparing the corresponding elements, we get,
2x + 12 = 0
thus, x = -6
6 + 6y = 0
thus, y = -1
Solution 30
Solution 31
(i) True.
Addition of matrices is commutative.
(ii) False.
Subtraction of matrices is not commutative.
(iii) True.
Multiplication of matrices is associative.
(iv) True.
Multiplication of matrices is distributive over addition.
(v) True.
Multiplication of matrices is distributive over subtraction.
(vi) True.
Multiplication of matrices is distributive over subtraction.
(vii) False.
Laws of algebra for factorization and expansion are not applicable to matrices.
(viii) False.
Laws of algebra for factorization and expansion are not applicable to matrices.
Matrices Exercise Ex. 9(D)
Solution 1
Comparing the corresponding elements, we get,
6x - 10 = 8
6x = 18
x = 3
-2x + 14 = 4y
4y = -6+ 14 = 8
y = 2
Solution 2
Comparing the corresponding elements, we get,
3x + 18 = 15
3x = -3
x = -1
12x + 77 = 10y
10y = -12 + 77 = 65
y = 6.5
Solution 3
(i) x, y Î W (whole numbers)
It can be observed that the above two equations are satisfied when x = 3 and y = 4.
(ii) x, y Î Z (integers)
It can be observed that the above two equations are satisfied when x = 
3 and y = 4.
Solution 4
(i)
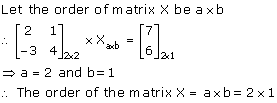
(ii)
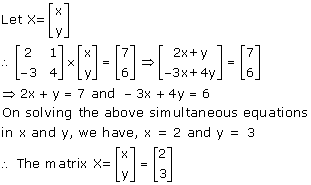
Solution 5
Solution 6
Let the order of matrix M be a x b.
3A x M = 2B
Clearly, the order of matrix M is 2 x 1.
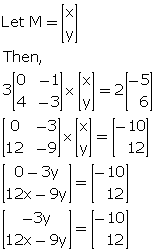
Comparing the corresponding elements, we get,
-3y = -10
y = 
12x - 9y = 12
Solution 7
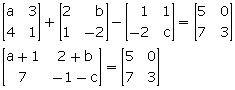
Comparing the corresponding elements, we get,
a + 1 = 5 
a = 4
2 + b = 0 b = -2
-1 - c = 3 c = -4
Solution 8
(i)
(ii)
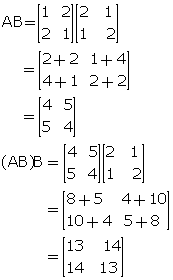
Solution 9
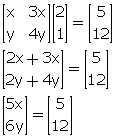
Comparing the corresponding elements, we get,
5x = 5
x = 1
6y = 12 y = 2
Solution 10
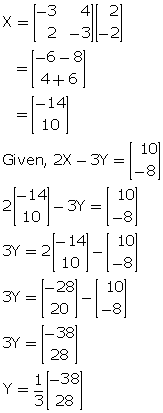
Solution 11
Given, A + X = 2B + C
Solution 12
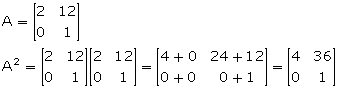
Given, A2 = B
Comparing the corresponding elements, we get,
x = 36
Solution 13
Solution 14
Solution 15
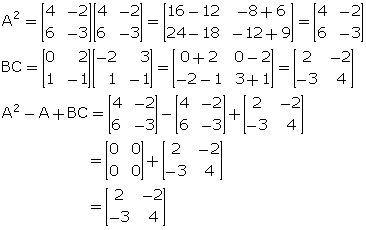
Solution 16
A = 
A2 = A 
A = 
= 
AB = A B = 
=
= 
B2 = B x B = 
= 
= 
A2 + AB + B2 = 
= 
Solution 17
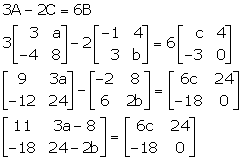
Comparing the corresponding elements, we get,
3a - 8 = 24 
3a = 32 a = 
24 - 2b = 0 2b = 24 b = 12
11 = 6c c = 
Solution 18
A = 
BA = 
C2 = 
BA = C2 
=
By comparing,
-2q = -8 q = 4
And p = 8
Solution 19
AB = 
Solution 20
= 
= 
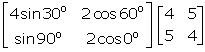
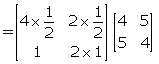
Solution 21
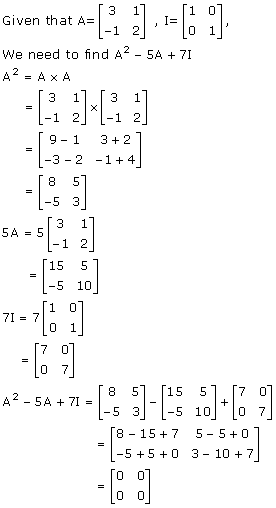
Solution 22
A2 = 9A + MI
⇒ A2 - 9A = mI ….(1)
Now, A2 = AA
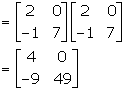
Substituting A2 in (1), we have
A2 - 9A = mI
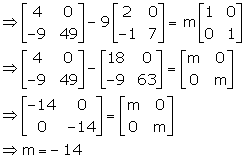
Solution 23
(i) Let the order of matrix X = m × n
Order of matrix A = 2 × 2
Order of matrix B = 2 × 1
Now, AX = B
∴ m = 2 and n = 1
Thus, order of matrix X = m × n = 2 × 1
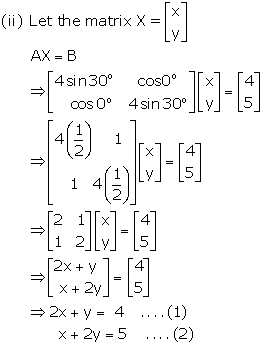
Multiplying (1) by 2, we get
4x + 2y = 8 ….(3)
Subtracting (2) from (3), we get
3x = 3
⇒ x = 1
Substituting the value of x in (1), we get
2(1) + y = 4
⇒ 2 + y = 4
⇒ y = 2
Solution 24
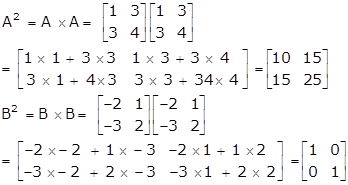
Given: A2 - 5B2 = 5C
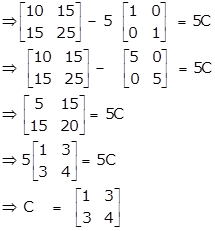
Solution 25
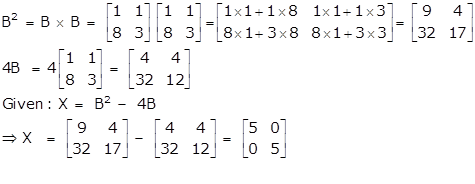
To find: a and b
