Class 10 SELINA Solutions Maths Chapter 16 - Loci (Locus and its Constructions)
Loci (Locus and its Constructions) Exercise Ex. 16(A)
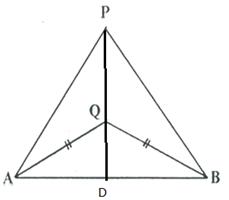
Solution 1
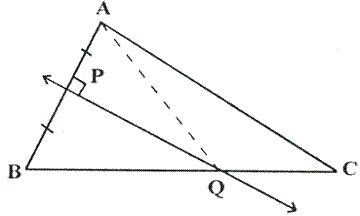
Construction: Join AQ
Proof: In 
and 
,
AP = BP (given)
(Each = 90
)
PQ = PQ (Common)
Hence Q is equidistant from A and B.
Solution 2
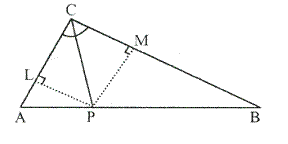
Construction: From P, draw 
and 
Proof: In 
and 
,
Hence, P is equidistant from AC and BC
Solution 3
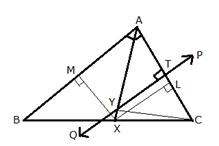
Construction: From X,
draw 
and 
. Also join YC.
Proof:
i) In 
and 
,
Hence, X is equidistant from AB and AC.
ii) In 
and 
,
Hence, Y is equidistant from A and C.
Solution 4
Given: In triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm
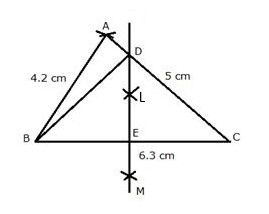
Steps of Construction:
i) Draw a line segment BC = 6.3 cm
ii) With centre B and radius 4.2 cm, draw an arc.
iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
iv) Join AB and AC.
is the required triangle.
v) Again with centre B and C and radius greater than 
, draw arcs which intersects each other at L and M.
vi) Join LM intersecting AC at D and BC at E.
vii) Join DB.
Proof: In 
and 
Hence, D is equidistant from B and C.
Solution 5
Construction: Join PQ which meets AB in D.
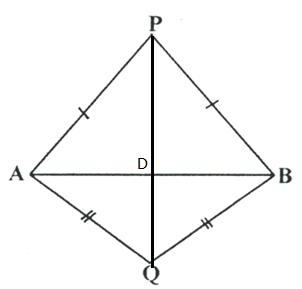
Proof: P is equidistant from A and B.
P lies on the perpendicular
bisector of AB.
Similarly, Q is equidistant from A and B.
Q lies on perpendicular bisector
of AB.
P and Q both lie on the
perpendicular bisector of AB.
PQ is perpendicular bisector of
AB.
Hence, locus of the points which are equidistant from two fixed points, is a perpendicular bisector of the line joining the fixed points.
Solution 6
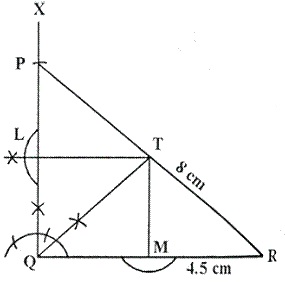
Steps of Construction:
i) Draw a line segment QR = 4.5 cm
ii) At Q, draw a ray QX making an angle of 
iii) With centre R and radius 8 cm, draw an arc which intersects QX at P.
iv) Join RP.
is the required triangle.
v) Draw the bisector of 
which meets PR in T.
vi) From T, draw perpendicular TL and TM respectively on PQ and QR.
Proof: In 
and 
Hence, T is equidistant from PQ and QR.
Solution 7
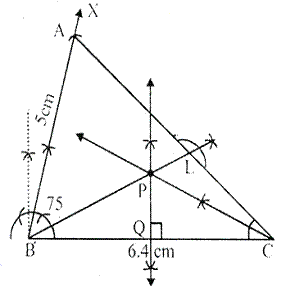
Steps of Construction:
i) Draw a line segment BC = 6.4 cm
ii) At B, draw a ray BX making an angle of 
with BC and cut off BA = 5 cm.
iii) Join AC.
is the required triangle.
iv) Draw the perpendicular bisector of BC.
v) Draw the angle bisector of angle ACB which intersects the perpendicular bisector of BC at P.
vi) Join PB and draw 
.
Proof: In 
and 
Hence, P is equidistant from B and C.
Again in 
and 
Hence, P is equidistant from AC and BC.
Solution 8
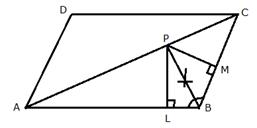
Construction: From P, draw 
and 
Proof: In 
and 
Hence, P is equidistant from AB and BC.
Solution 9
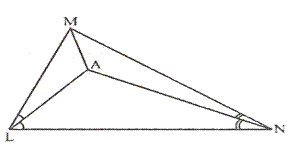
Construction: Join AM
Proof:
A lies on bisector of 
A is equidistant from MN and LN.
Again, A lies on bisector of 
A is equidistant from LN and LM.
Hence, A is equidistant from all sides of the triangle LMN.
Also, A is equidistant from MN and LM.
A lies on the bisector of 
Solution 10
Steps of construction:
(i)Draw line BC = 6 cm and an angle CBX = 60o. Cut off AB = 3.5. Join AC, triangle ABC is the required triangle.
(ii) Draw the angle bisector of angle B
(iii) Draw the perpendicular bisector of BC
(iiv)Bisector of angle B meets bisector of BC at P.
BP is the required length, where, PB = 3.5 cm
P is the point which is equidistant from BA and BC, also equidistant from B and C.
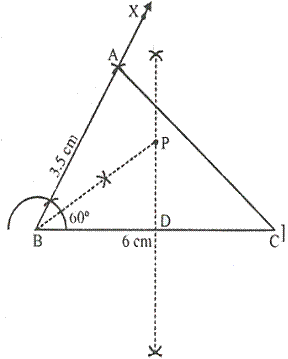
PB=3.6 cm
Solution 11
i)
Construction: Join FB and FC
Proof: In 
and 
Hence, F is equidistant from A and B.
ii)
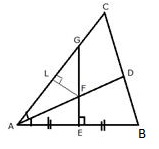
Construction: Draw 
Proof: In 
and 
Hence, F is equidistant from AB and AC.
Solution 12
Since P lies on the bisector of angle B,
therefore, P is equidistant from AB and BC .... (1)
Similarly, P lies on the bisector of angle C,
therefore, P is equidistant from BC and CD .... (2)
From (1) and (2),
Hence, P is equidistant from AB and CD.
Solution 13
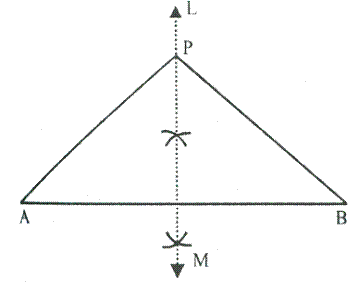
Steps of construction:
(i) Draw a line segment AB of 6 cm.
(ii) Draw perpendicular bisector LM of AB. LM is the required locus.
(iii) Take any point on LM say P.
(iv) Join PA and PB.
Since, P lies on the perpendicular bisector of line AB.
Therefore, P is equidistant from A and B.
i.e. PA = PB
Hence, Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.
Solution 14
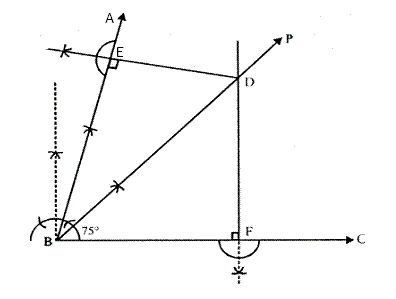
Steps of Construction:
i) Draw a ray BC.
ii) Construct a ray BA making an angle of 
with BC. Therefore, 
.
iii) Draw the angle bisector BP of 
.
BP is the required locus.
iv) Take any point D on BP.
v) From D, draw 
and 
Since D lies on the angle bisector BP of
D is equidistant from AB and BC.
Hence, DE = DF
Similarly, any point on BP is equidistant from AB and BC.
Therefore, BP is the locus of all points which are equidistant from AB and BC.
Solution 15
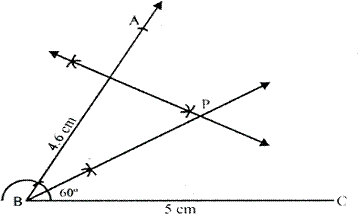
Steps of Construction:
i) Draw a line segment BC = 5 cm
ii) At B, draw a ray BX making an
angle of 
and cut off BA = 4.6
cm.
iii) Draw the angle bisector of 
.
iv) Draw the perpendicular bisector of AB which intersects the angle bisector at P.
P is the required point which is equidistant from AB and BC, as well as from A and B.
Solution 16
Steps of Construction:
i) AB and CD are the two lines given.
ii) Draw a perpendicular bisector of line AB which intersects CD in P.
P is the required point which is equidistant from A and B.
Since P lies on perpendicular bisector of AB; PA = PB.
Solution 17
Steps of Construction:
i) In the given triangle, draw the
angle bisector of 
.
ii) Draw the perpendicular bisector of BC which intersects the angle bisector at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
Since P lies on angle bisector of ,
It is equidistant from AB and AC.
Again, P lies on perpendicular bisector of BC,
Therefore, it is equidistant from B and C.
Solution 18
Steps of Construction:
1) Draw a line segment AB = 7 cm.
2) Draw angle 
with the help of compass.
3)Cut off BC = 8 cm.
4)Join A and C.
5)The triangle ABC so formed is the required triangle.
i) Draw the perpendicular bisector of BC. The point situated on this line will be equidistant from B and C.
ii) Draw the angle bisector of 
. Any point situated on this angular bisector is equidistant from lines AB and BC.
The point which fulfills the condition required in (i) and (ii) is the intersection point of bisector of line BC and angular bisector of .
P is the required point which is equidistant from AB and AC as well as from B and C.
On measuring the length of line segment PB, it is equal to 4.5 cm.
Solution 19
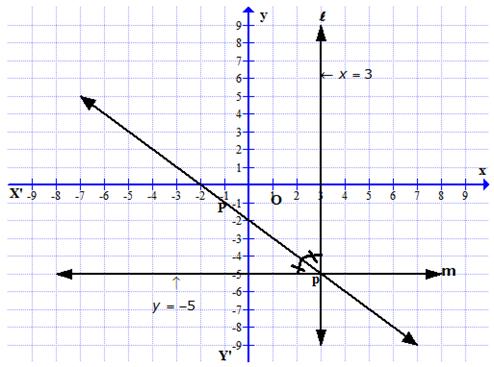
On the graph, draw axis XOX’ and YOY’
Draw a line l, x = 3 which is parallel to y-axis
And draw another line m, y = -5, which is parallel to x-axis
These two lines intersect each other at P.
Now draw the angle bisector p of angle P.
Since p is the angle bisector, any point on p is equidistant from l and m.
Therefore, this line p is equidistant from l and m.
Solution 20
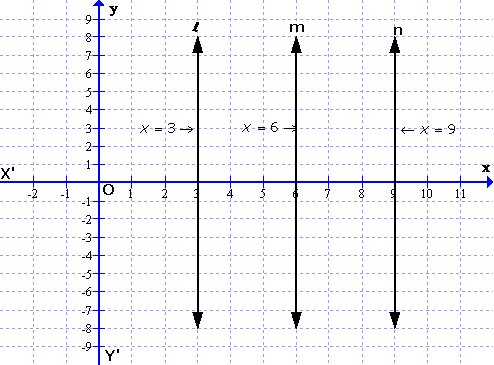
On the graph, draw axis XOX’ and YOY’
Draw a line m, x = 6 which is parallel to y-axis
Take points P and Q which are at a distance of 3 units from the line m.
Draw lines l and n from P and Q parallel to m
With locus = 3, two lines can be drawn x = 3 and x = 9.
Loci (Locus and its Constructions) Exercise Ex. 16(B)
Solution 1
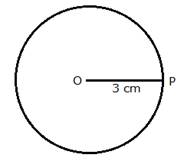
The locus of a point which is 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is the centre of the circle.
Solution 2
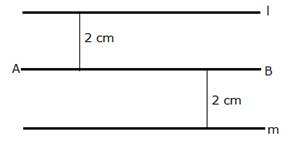
The locus of a point at a distance of 2 cm from a fixed line AB is a pair of straight lines l and m which are parallel to the given line at a distance of 2 cm.
Solution 3
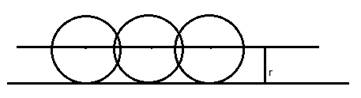
The locus of the centre of a wheel, which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.
Solution 4
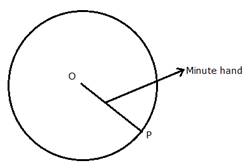
The locus of the moving end of the minute hand of the clock will be a circle where radius will be the length of the minute hand.
Solution 5
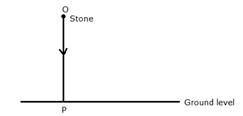
The locus of a stone which is dropped from the top of a tower will be a vertical line through the point from which the stone is dropped.
Solution 6
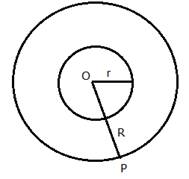
The locus of the runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge will be the circumference of a circle whose radius is equal to the radius of the inner circular track plus 1.5 m.
Solution 7
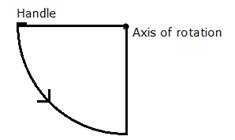
The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.
Solution 8
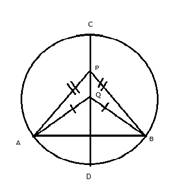
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be the diameter which is perpendicular bisector of the line joining the two fixed points on the circle.
Solution 9
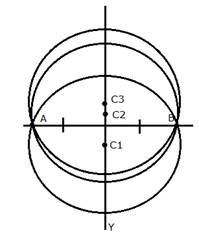
The locus of the centre of all the circles which pass through two fixed points will be the perpendicular bisector of the line segment joining the two given fixed points.
Solution 10
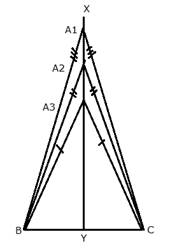
The locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.
Solution 11
The locus of a point in space is the surface of the sphere whose centre is the fixed point and radius equal to 4 cm.
Solution 12
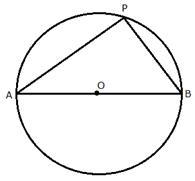
The locus of the point P is the
circumference of a circle with AB as diameter and satisfies the condition 
.
Solution 13
i)
The locus of the point in a rhombus ABCD which is equidistant from AB and BC will be the diagonal BD.
ii)
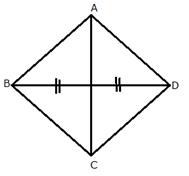
The locus of the point in a rhombus ABCD which is equidistant from B and D will be the diagonal AC.
Solution 14
The locus of all the people on Earth's surface is the circumference of a circle whose radius is 332 m and centre is the point where the gun is fired.
Solution 15
i) The locus is the space inside of the circle whose radius is 3 cm and the centre is the fixed point which is given.
ii) The locus is the space outside of the circle whose radius is 4 cm and centre is the fixed point which is given.
iii) The locus is the space inside and circumference of the circle with a radius of 2.5 cm and the centre is the given fixed point.
iv) The locus is the space outside and circumference of the circle with a radius of 35 mm and the centre is the given fixed point.
v) The locus is the circumference of the circle concentric with the second circle whose radius is equal to the sum of the radii of the two given circles.
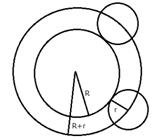
vi) The locus of the centre of all circles whose tangents are the arms of a given angle is the bisector of that angle.
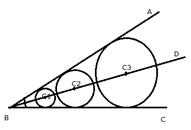
vii) The locus of the mid-points of the chords which are parallel to a given chords is the diameter perpendicular to the given chords.
viii) The locus of the points within a circle which are equidistant from the end points of a given chord is the diameter which is perpendicular bisector of the given chord.
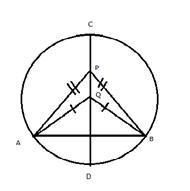
Solution 16
Draw a line XY parallel to the base BC from the vertex A.
This line is the locus of vertex A of all the triangles which have the base BC and length of altitude equal to AD.
Solution 17
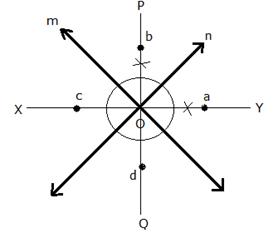
Draw an angle bisector PQ and XY of angles formed by the lines m and n. From O, draw arcs with radius 2.5 cm, which intersect the angle bisectors at a, b, c and d respectively.
Hence, a, b, c and d are the required four points.
Solution 18
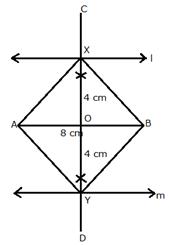
(i)Draw a line segment AB = 8 cm.
(ii)Draw two parallel lines l and m to AB at a distance of 4 cm.
(iii)Draw the perpendicular bisector of AB which intersects the parallel lines l and m at X and Y respectively then, X and Y are the required points.
(iv)Join AX, AY, BX and BY.
The figure AXBY is a square as its diagonals are equal and intersect at 90o.
Solution 19
i) Draw an angle of 
with AB = BC = 8 cm
ii) Draw the angle bisector BX of 
iii) With centre M and N, draw circles of radius equal to 4 cm, which intersects each other at P. P is the required point.
iv) Join MP, NP
BMPN is a rhombus since MP = BM = NB = NP = 4 cm
Solution 20
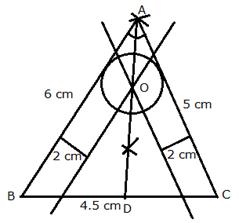
Steps of Construction:
i) Draw a line segment BC = 4.5 cm
ii) With B as centre and radius 6 cm and C as centre and radius 5 cm, draw arcs which intersect each other at A.
iii) Join AB and AC.
ABC is the required triangle.
iv) Draw the angle bisector of 
v) Draw lines parallel to AB and AC at a distance of 2 cm, which intersect each other and AD at O.
vi) With centre O and radius 2 cm, draw a circle which touches AB and AC.
Solution 21
Steps of Construction:
i) Draw a line segment AB = 4.8 cm
ii) At A, draw a ray AX making an angle of 
iii) Cut off AC = 4 cm from AX
iv) Join BC.
ABC is the required triangle.
v) Draw two lines l and m parallel to BC at a distance of 1.2 cm
vi) Draw the perpendicular bisector of BC which intersects l and m at P and P’
P and P’ are the required points which are inside and outside the given triangle ABC.
Solution 22
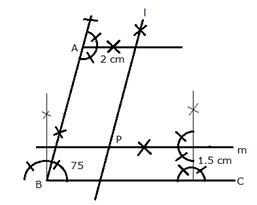
Steps of Construction:
i) Draw a ray BC.
ii) At B, draw a ray BA making an
angle of 
with BC.
iii) Draw a line l parallel to AB at a distance of 2 cm
iv) Draw another line m parallel to BC at a distance of 1.5 cm which intersects line l at P.
P is the required point.
Solution 23
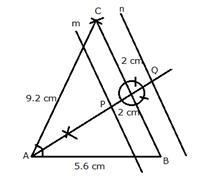
Steps of Construction:
i) Draw a line segment AB = 5.6 cm
ii) From A and B, as centers and radius 9.2 cm, make two arcs which intersect each other at C.
iii) Join CA and CB.
iv) Draw two lines n and m parallel to BC at a distance of 2 cm
v) Draw the angle bisector of 
which intersects m and
n at P and Q respectively.
P and Q are the required points which are equidistant from AB and AC.
On measuring the distance between P and Q is 4.3 cm.
Solution 24
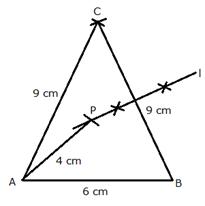
Steps of Construction:
i) Draw a line segment AB = 6 cm
ii) With A and B as centers and radius 9 cm, draw two arcs which intersect each other at C.
iii) Join AC and BC.
iv) Draw the perpendicular bisector of BC.
v) With A as centre and radius 4 cm, draw an arc which intersects the perpendicular bisector of BC at P.
P is the required point which is equidistant from B and C and at a distance of 4 cm from A.
Solution 25
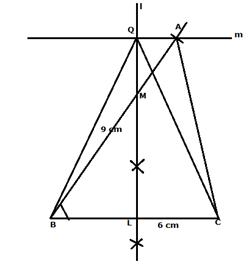
Steps of Construction:
(i) Draw a line segment BC = 6 cm.
(ii) At B, draw a ray BX making an angle 60 degree and cut off BA=9 cm.
(iii) Join AC. ABC is the required triangle.
(iv) Draw perpendicular bisector of BC which intersects BA in M, then any point on LM is equidistant from B and C.
(v) Through A, draw a line m || BC.
(vi) The perpendicular bisector of BC and the parallel line m intersect each other at Q.
(vii) The isosceles triangle QBC is equal in area to triangle ABC. m is the locus of all points through which any triangle with base BC will be equal in area of triangle ABC.
On measuring CQ = 8.4 cm.
Solution 26
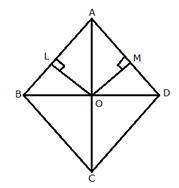
Steps of Construction:
i) In rhombus ABCD, draw angle
bisector of 
which meets
in C.
ii) Join BD, which intersects AC at O.
O is the required locus.
iii) From O, draw 
and 
In 
( AC is bisector of angle A)
AO = OA (Common)
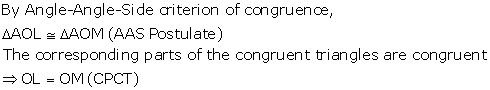
Therefore, O is equidistant from AB and AD.
Diagonal AC and BD bisect each other at right angles at O.
Therefore, AO = OC
Hence, O is equidistant from A and C.
Solution 27
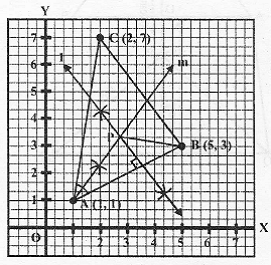
Steps of Construction:
i) Plot the points A(1,1), B(5,3) and C(2,7) on the graph and join AB, BC and CA.
ii) Draw the perpendicular bisector of AB and angle bisector of angle A which intersect each other at P.
P is the required point.
Since P lies on the perpendicular bisector of AB.
Therefore, P is equidistant from A and B.
Again,
Since P lies on the angle bisector of angle A.
Therefore, P is equidistant from AB and AC.
On measuring, the length of PA = 5.2 cm
Solution 28
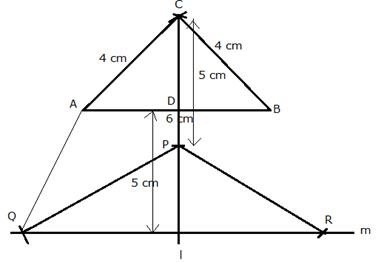
Steps of Construction:
i) Draw a line segment AB = 6 cm.
ii) With centers A and B and radius 4 cm, draw two arcs which intersect each other at C.
iii) Join CA and CB.
iv) Draw the angle bisector of angle C and cut off CP = 5 cm.
v) A line m is drawn parallel to AB at a distance of 5 cm.
vi) P as centre and radius 5 cm, draw arcs which intersect the line m at Q and R.
vii) Join PQ, PR and AQ.
Q and R are the required points.
Solution 29
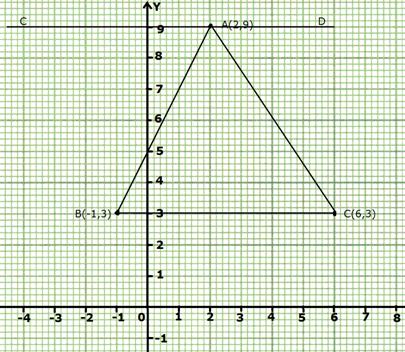
Steps of construction:
i) Plot the given points on graph paper.
ii) Join AB, BC and AC.
iii) Draw a line parallel to BC at A and mark it as CD.
CD is the required locus of point A where area of triangle ABC remains same on moving point A.
Solution 30
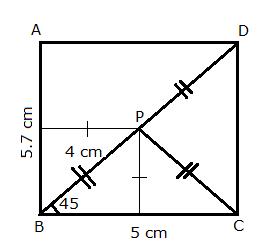
i) Steps of Construction:
1) Draw a line segment BC = 5 cm
2) B as centre and radius 4 cm draw an arc at an angle of 45 degrees from BC.
3) Join PC.
4) B and C as centers, draw two perpendiculars to BC.
5) P as centre and radius PC, cut an arc on the perpendicular on C at D.
6) D as centre, draw a line parallel to BC which intersects the perpendicular on B at A.
ABCD is the required rectangle such that P is equidistant from AB and BC (since BD is angle bisector of angle B) as well as C and D.
ii) On measuring AB = 5.7 cm
Solution 31
i. Steps of construction:
1. Draw BC = 6.5 cm using a ruler.
2. With B as center and radius equal to approximately half of BC, draw an arc that cuts the segment BC at Q.
3. With Q as center and same radius, cut the previous arc at P.
4. Join BP and extend it.
5. With B as center and radius 5 cm, draw an arc that cuts the arm PB to obtain point A.
6. Join AC to obtain ΔABC.
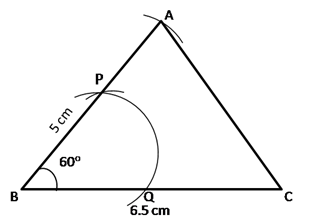
ii. With A as center and radius 3.5 cm, draw a circle.
The circumference of a circle is the required locus.
iii. Draw CH, which is bisector of angle ACB. CH is the required locus.
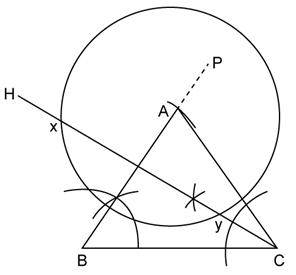
iv. Circle with center A having radius 3.5cm and line CH meet at points X and Y as shown in the figure. xy = 8.2 cm (approximately)
