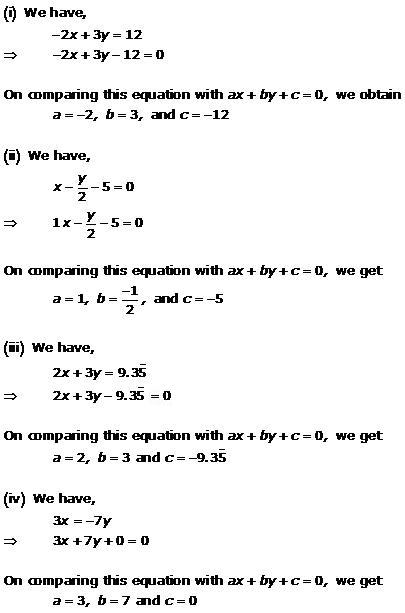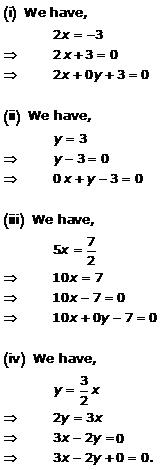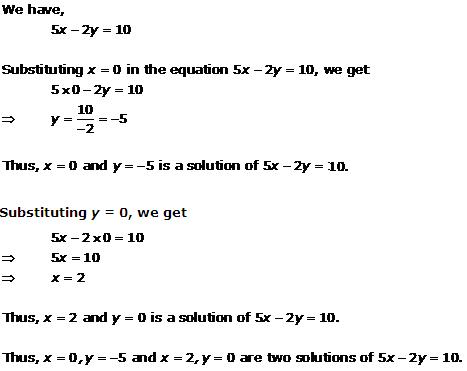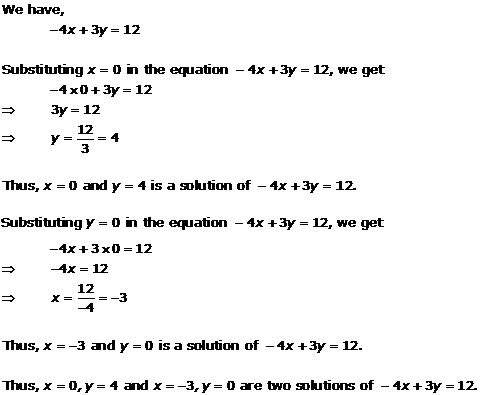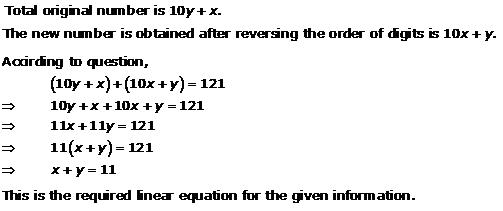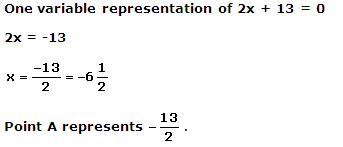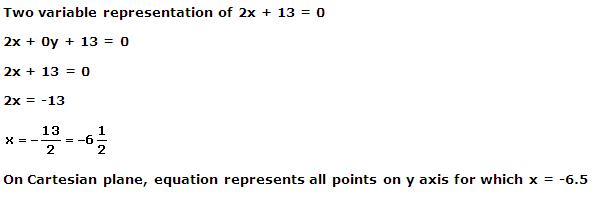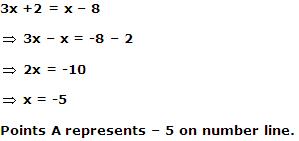Class 9 RD SHARMA Solutions Maths Chapter 7 - Linear Equations in Two Variables
Linear Equations in Two Variables Exercise Ex. 7.1
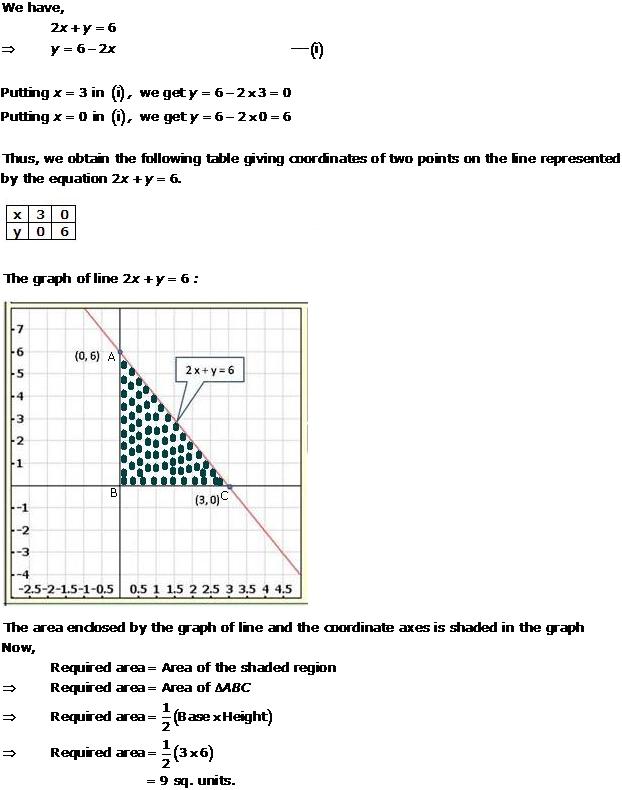
Solution 1
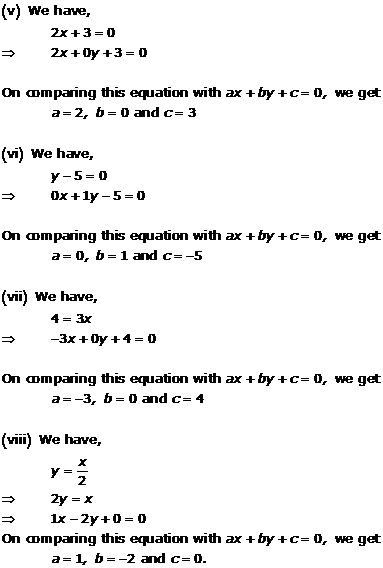
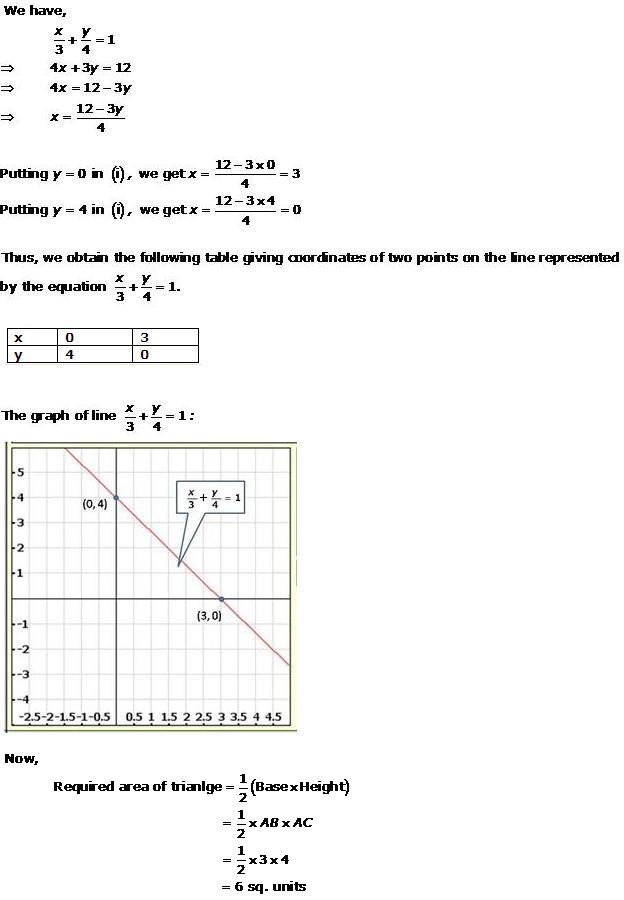
Solution 2
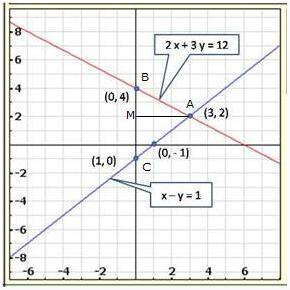
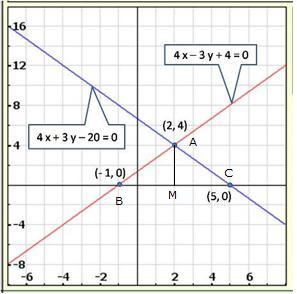
Solution 3

Linear Equations in Two Variables Exercise Ex. 7.2
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)
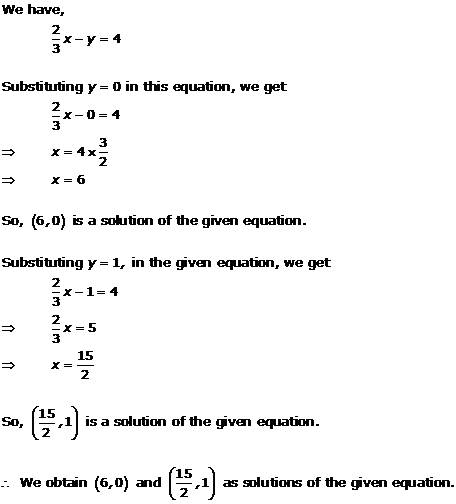
Solution 2

Solution 3
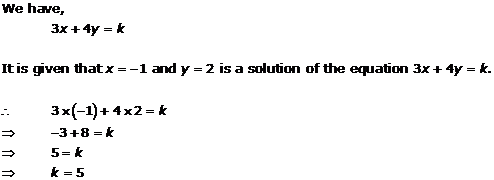
Solution 4
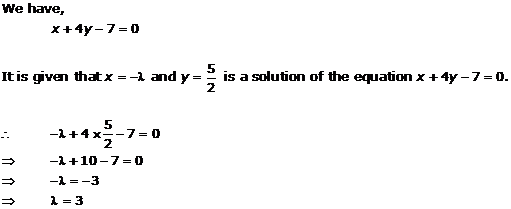
Solution 5
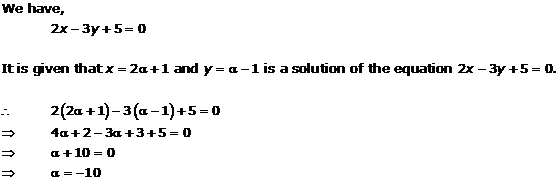
Solution 6
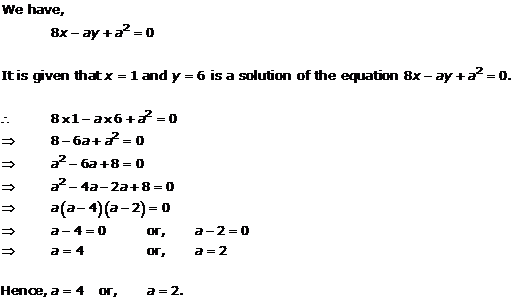
Solution 7(i)
Solution 7(ii)
Solution 7(iii)
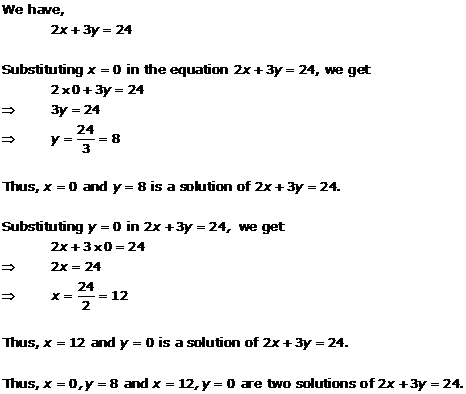
Linear Equations in Two Variables Exercise Ex. 7.3
Solution 1(i)


Solution 1(ii)

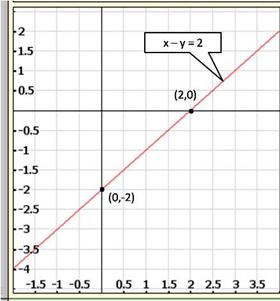
Solution 1(iii)

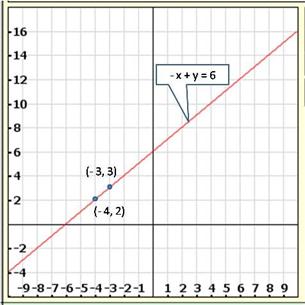
Solution 1(iv)


Solution 1(v)

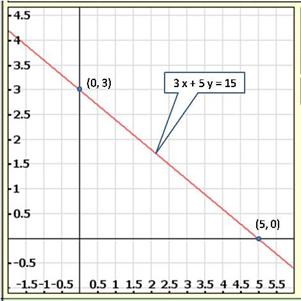
Solution 1(vi)
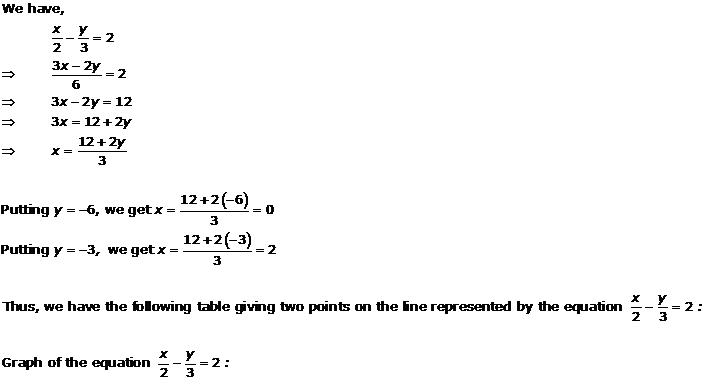
Solution 1(vii)
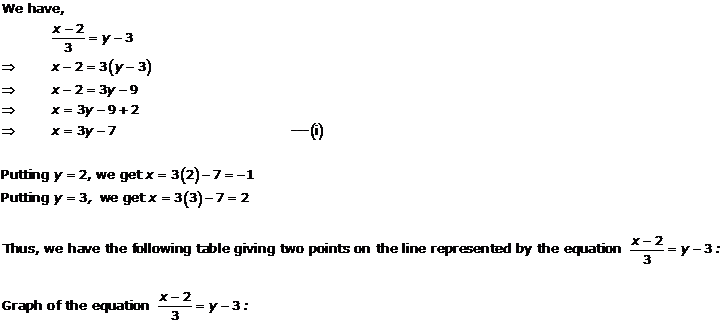
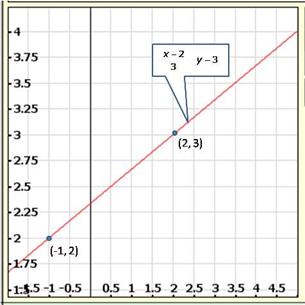
Solution 1(viii)

Solution 2

Solution 3

Solution 4
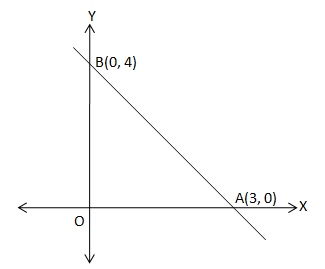
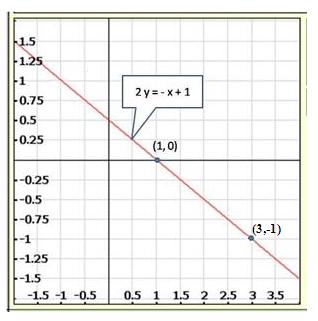
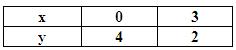
The given points on the graph:
It is dear from the graph, the straight line passing through these points also passes through the point (1,4).
Solution 5
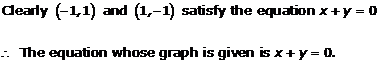
Solution 6
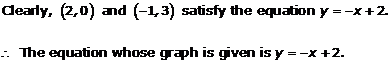
Solution 7
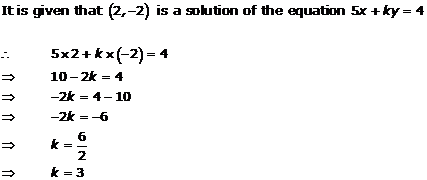
Solution 8
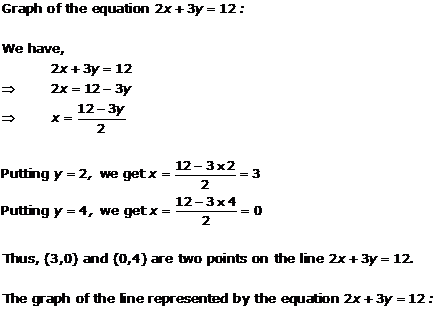
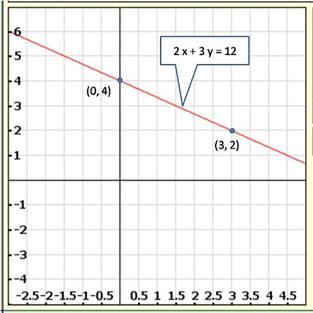
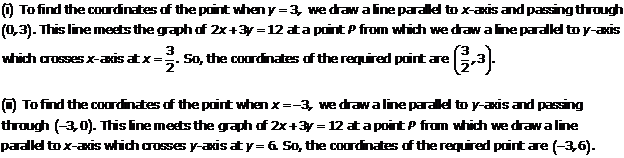
Solution 9(i)
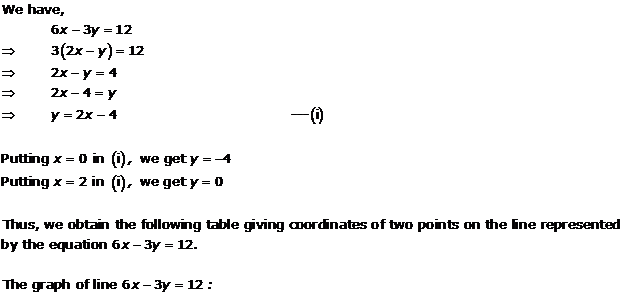
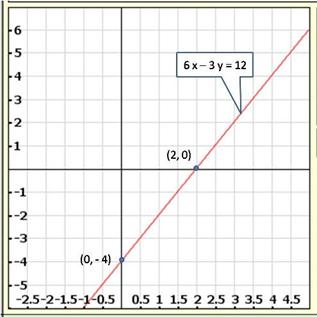
Solution 9(ii)
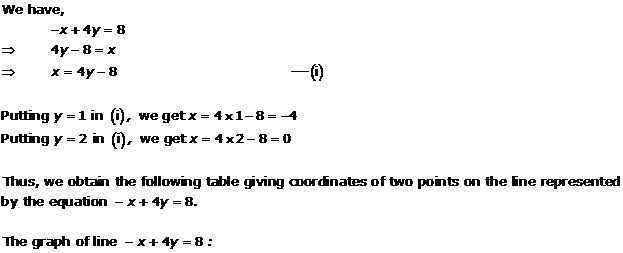
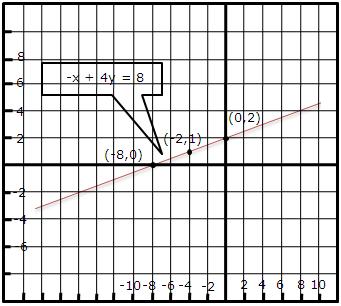
Solution 9(iii)

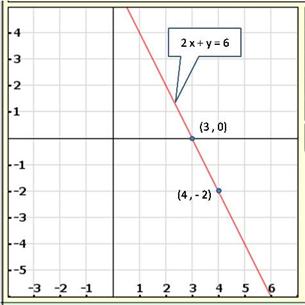
Solution 9(iv)


Solution 10

Solution 11
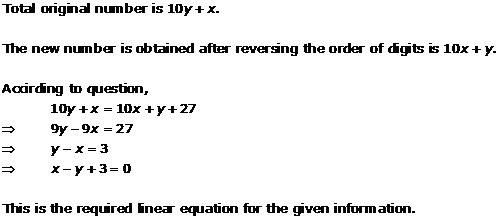
Solution 12
Solution 13
Solution 14
Solution 15
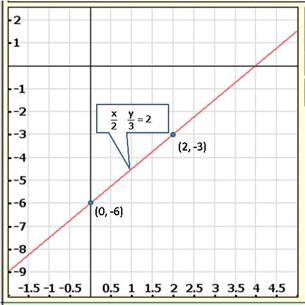
We have,
y = |X| ...(i)
Putting x = 0, we get y = 0
Putting x = 2, we get y = 2
Putting x = -2, we get y = 2
Thus, we have the following table for the points on graph of |x|.
| x | 0 | 2 | -2 |
| y | 0 | 2 | 2 |
The graph of the equation y = |x|: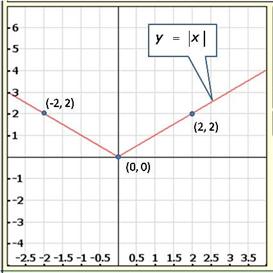
Solution 16
We have,
y = |x| + 2 ...(i)
Putting x = 0, we get y = 2
Putting x = 1, we get y = 3
Putting x = -1, we get y = 3
Thus, we have the following table for the points on graph of |x| + 2:
| x | 0 | 1 | -1 |
| y | 2 | 3 | 3 |
The graph of the equation y = |x| + 2: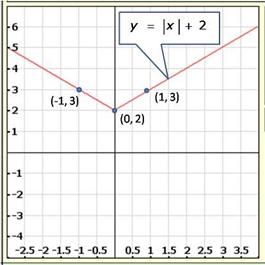
Solution 17
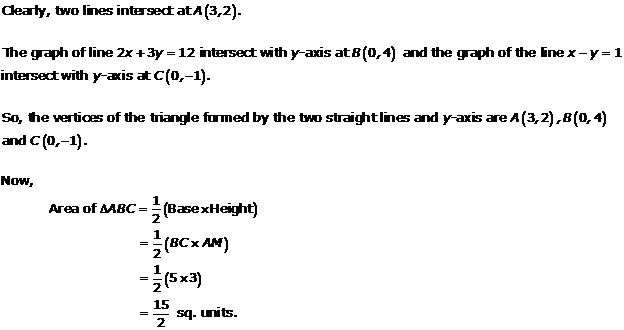
Solution 18
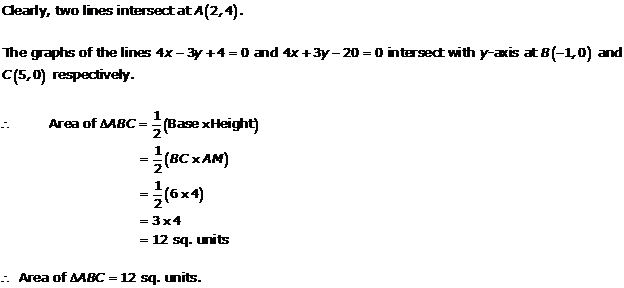
Solution 19
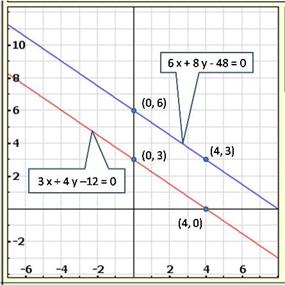
Solution 20
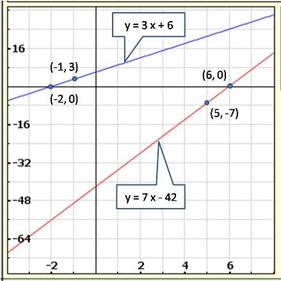
Solution 21
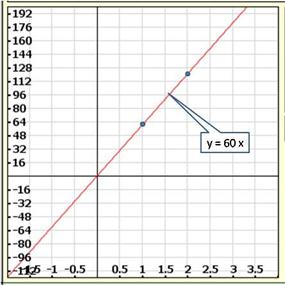

Linear Equations in Two Variables Exercise Ex. 7.4
Solution 1(i)
Solution 1(ii)
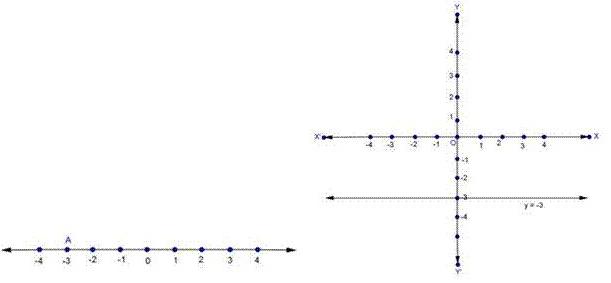
y + 3 = 0
y = -3
Point A represents -3 on number line.
On Cartesian plane, equation represents all points on x axis for which y = -3
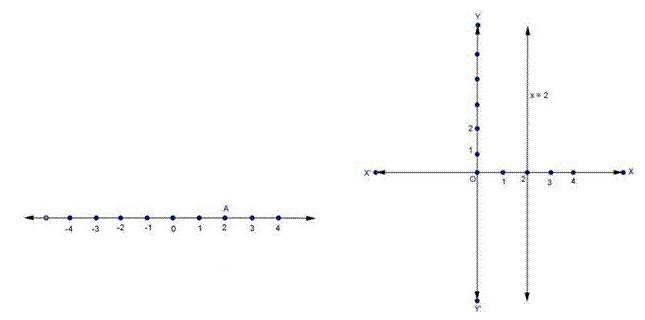
Solution 1(iii)
y = 3
Point A represents 3 on number line.
On Cartesian plane, equation represents all points on x axis for which y = 3
Solution 1(iv)
Solution 1(v)
Solution 2(i)
Solution 2(ii)
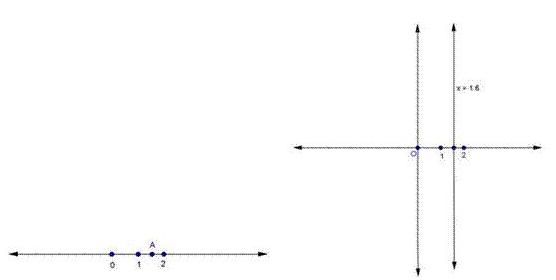
Solution 3(i)
Solution 3(ii)
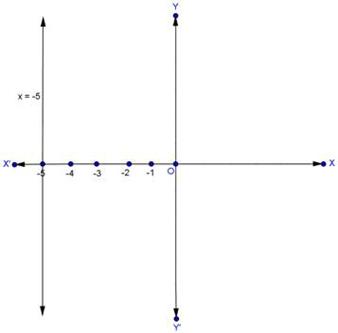
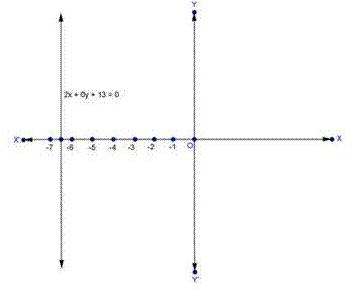
On Cartesian plane, equation represents all points on y axis for which x = -5
Solution 4
(i) The equation of the line that is parallel to x-axis and passing through the point (0,3) is y = 3
(ii) The equation of the line that is parallel to x-axis and passing through the point (0,-4) is y = -4
(iii) The equation of the line that is parallel to x-axis and passing through the point (2,-5) is y = -5
(iv) The equation of the line that is parallel to x-axis and passing through the point (3, 4) is y = 4
Solution 5

Linear Equations in Two Variables Exercise 7.33
Solution 1
y = ax + 3
If (4, 19) is its solution, then it must satisfy the equation.
Thus, we have
19 = a × 4 + 3
i.e. 4a = 16
i.e. a = 4
Hence, correct option is (b).
Solution 2
3x + y = 10
If (a, 4) lies on its graph, then it must satisfy the equation.
Thus, we have
3(a) + 4 = 10
i.e. 3a = 6
i.e. a = 2
Hence, correct option is (c).
Solution 3
On x-axis, the y-co-ordinate is always 0.
So, 2x - y = 4 will cut the x-axis where y = 0
i.e. 2x = 4
i.e. x = 2
Thus, 2x - y = 4 will cut the x-axis at (2, 0).
Hence, correct option is (a).
Solution 4
From Point (2, -3) there are infinitely many lines passing in every-direction.
So (2, -3) is satisfied with infinite linear equations.
Hence, correct option is (d).
Solution 5
Given equation is x – 2 = 0.
If this is treated as an equation in one variable x only, then it has the unique solution x = 2, which is a point on the number line.
However, when treated as an equation in two variables, it can be expressed as x - 2 = 0.
So as, an equation in two variables, x – 2 = 0 is represented by a single line parallel to y-axis at a distance of 2 units.
Hence, correct option is (a).
Solution 6
Substituting x = 2 and y = -1 in the following equations:
L.H.S. = x + 2y = 2 + 2(-1) = 2 - 2 = 0 = R.H.S.
L.H.S. = x + 2y = 2 + 2(-1) = 2 - 2 = 0 ≠ 4 ≠ R.H.S.
L.H.S. = 2x + y = 2(2) + (-1) = 4 - 1 = 3 ≠ 0 ≠ R.H.S.
L.H.S. = 2x + y = 2(2) + (-1) = 4 - 1 = 3 ≠ 5 ≠ R.H.S.
Hence, correct option is (a).
Solution 7
If (2k - 1, k) is solution of equation 10x - 9y = 12, then it must satisfy this equation.
Thus, we have
10(2k - 1) - 9k = 12
20k - 10 - 9k = 12
11k = 22
k = 2
Hence, correct option is (b).
Solution 8
The distance between the graph of the equations x = -3 and x = 2
= 2 - (-3)
= 2 + 3
= 5
Hence, correct option is (d).
Solution 9
The distance between given two graphs
= 3 - (-1)
= 3 + 1
= 4
Hence, correct option is (b).
Solution 10