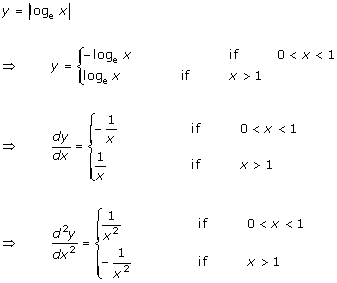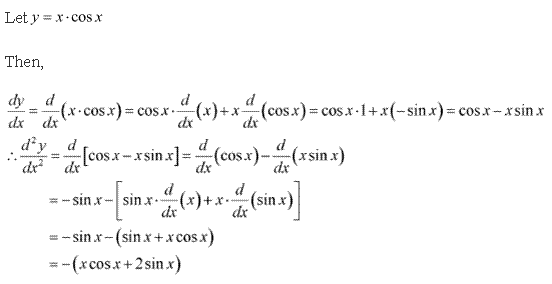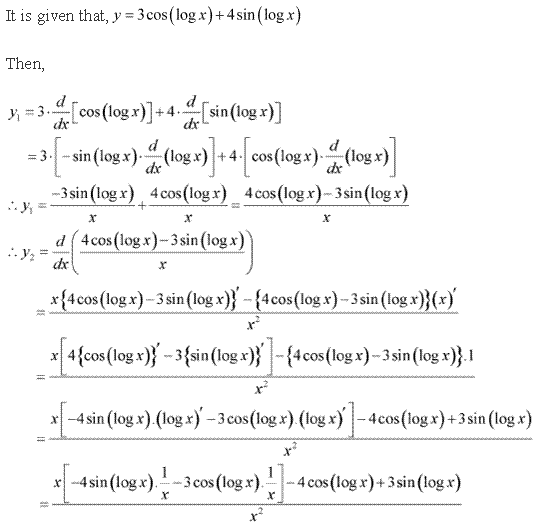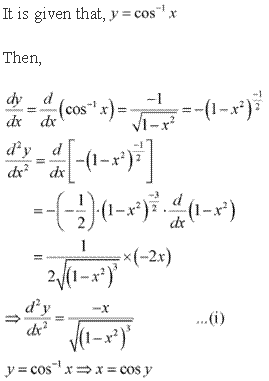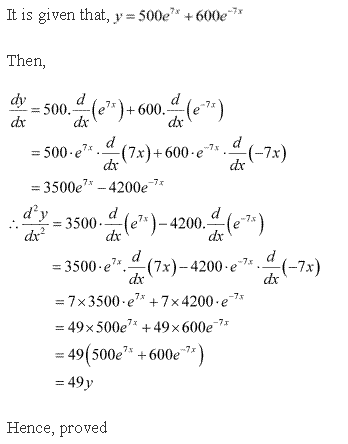Class 12-science RD SHARMA Solutions Maths Chapter 12 - Higher Order Derivatives
Ex. 12.1
MCQ
Ex. 12VSAQ
Higher Order Derivatives Exercise Ex. 12.1
Solution 1(i)
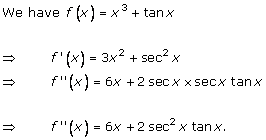
Solution 1(ii)

Solution 1(iii)

Solution 1(iv)
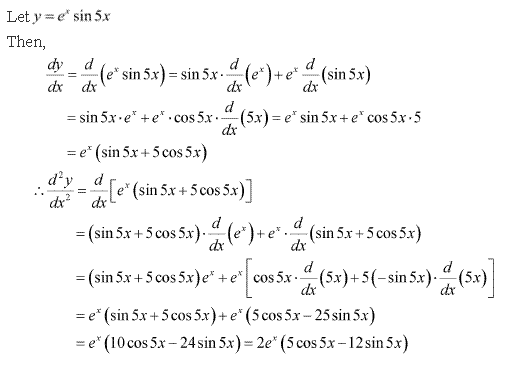
Solution 1(v)
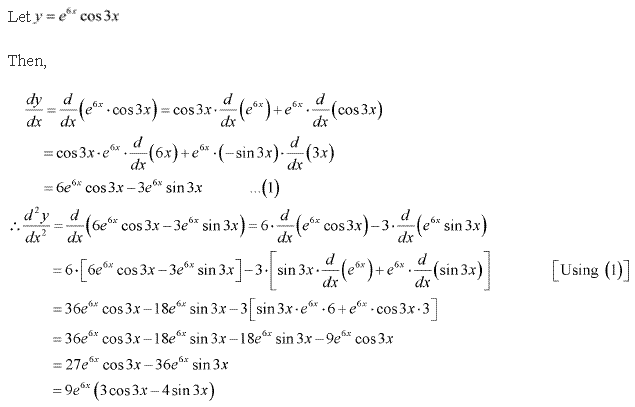
Solution 1(vi)

Solution 1(vii)
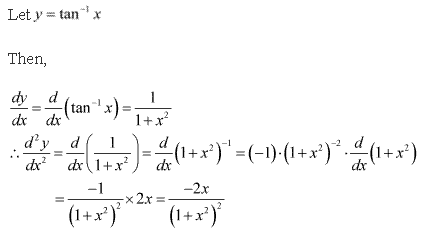
Solution 1(viii)
![]()
Solution 1(ix)
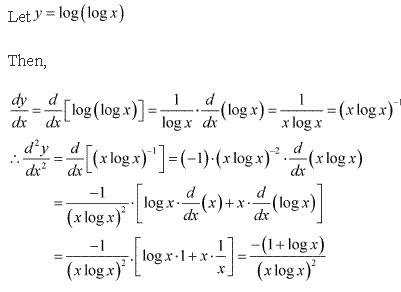
Solution 2

Solution 3

Solution 4

Solution 5

![]()
Solution 6
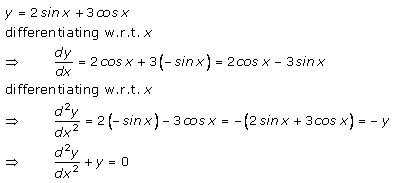
Solution 7

Solution 8

Solution 9
Given: ![]()
Differentiating
'x' w.r.t ![]() we get
we get
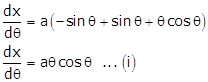
Differentiating
'y' w.r.t ![]() we get
we get
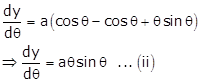
Dividing (ii) by (i), we get
![]() … (iii)
… (iii)
Differentiating above equation w.r.t x, we get
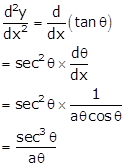
Hence, ![]()
Solution 10

Solution 11
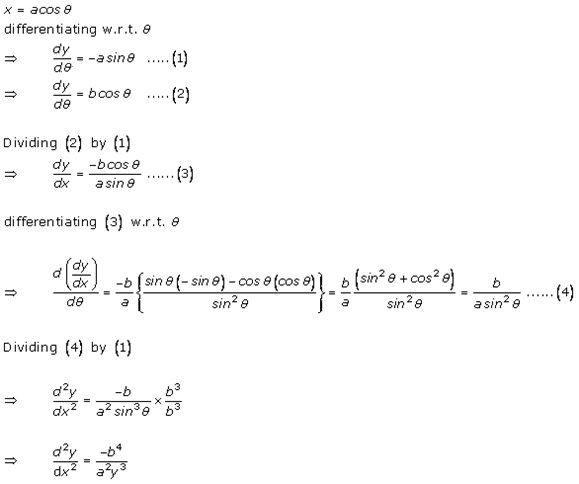
Solution 12

Solution 13
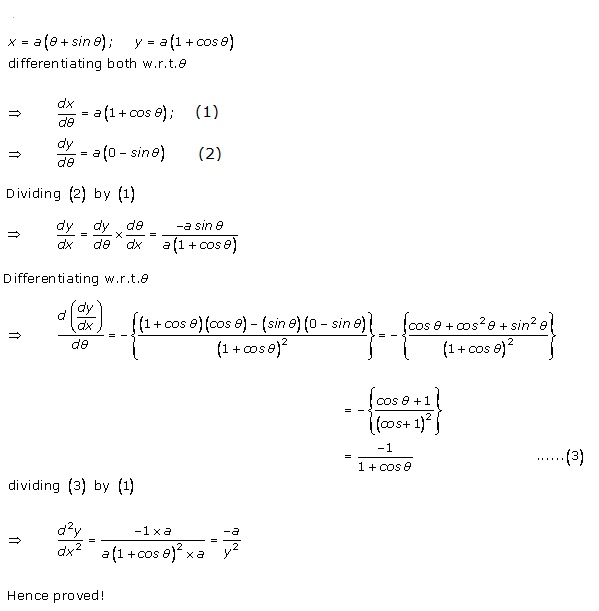
Solution 14

Solution 15

Solution 16

Solution 17


Solution 18

Solution 19
Solution 20

Solution 21
Solution 22
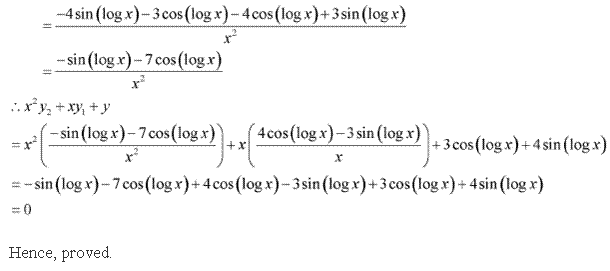
Solution 23

Solution 24
Solution 25

Solution 26

Solution 27

Solution 28
Solution 29

Solution 30
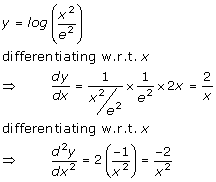
Solution 31

Solution 32

Solution 33
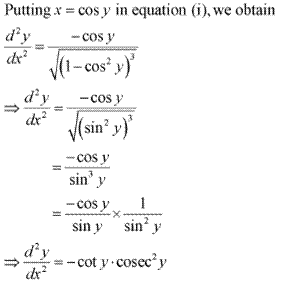
Solution 34

Solution 35
Solution 36
Solution 37

Solution 38

Solution 39

Solution 40
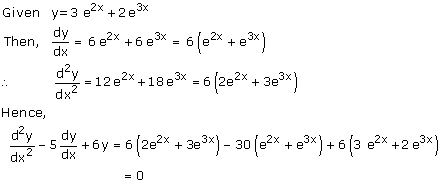
Solution 41

Solution 42

Solution 43



Solution 44

Solution 45

Solution 46

Solution 47
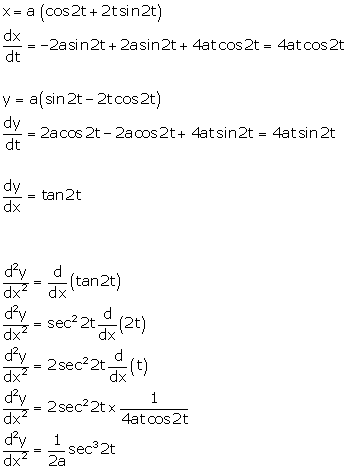
Solution 48
Given: ![]()
Differentiating 'x' w.r.t t, we get
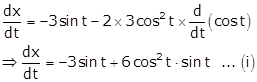
Differentiating 'y' w.r.t t, we get
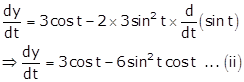
Dividing (ii) by (i), we get
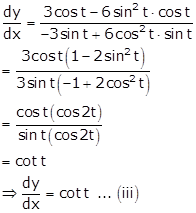
Differentiating above equation w.r.t x, we get
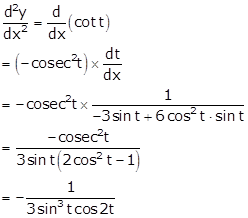
Hence, ![]()
Solution 49
Solution 50

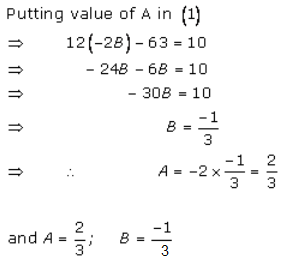
Solution 51
Solution 52

Solution 53
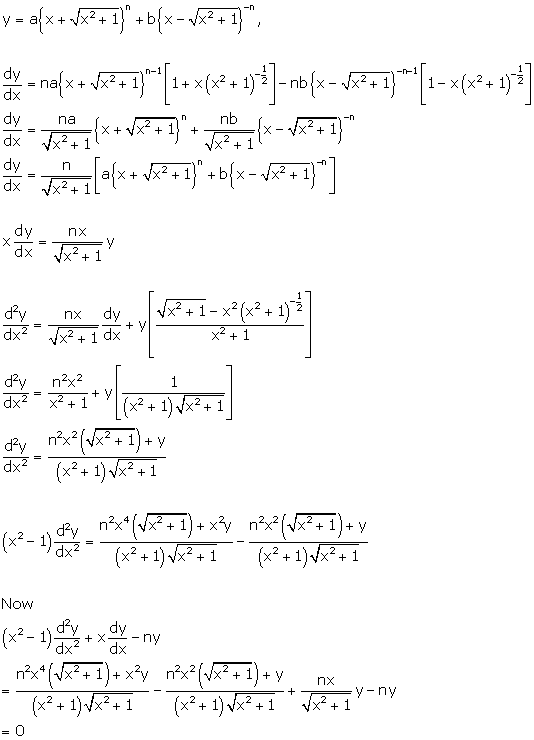
Higher Order Derivatives Exercise MCQ
Solution 1
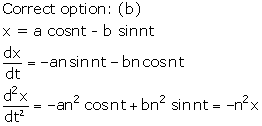
Solution 2

Solution 3
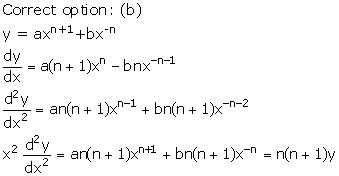
Solution 4
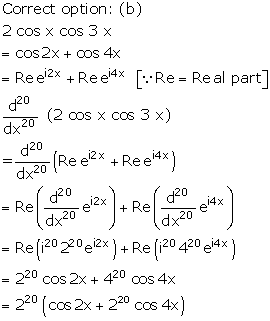
Solution 5
Correct option: (d)
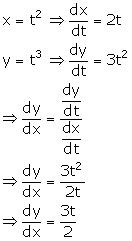
Solution 6
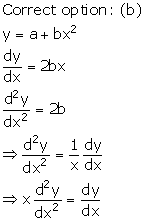
Solution 7

Solution 8
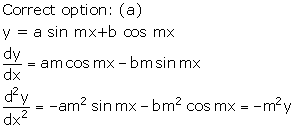
Solution 9
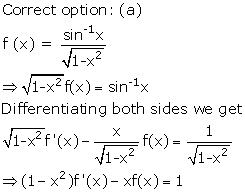
Solution 10
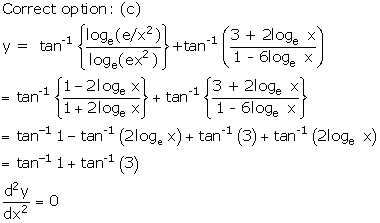
Solution 11

Solution 12

Solution 13

Solution 14
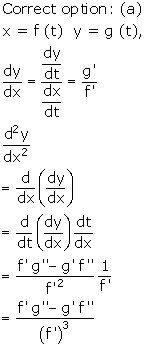
Solution 15
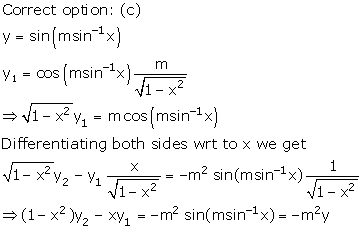
Solution 16
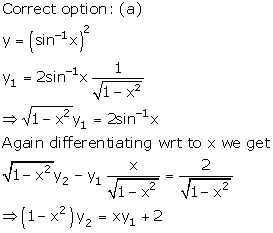
Solution 17

Solution 18
Question is incorrect.
![]()
Solution 19
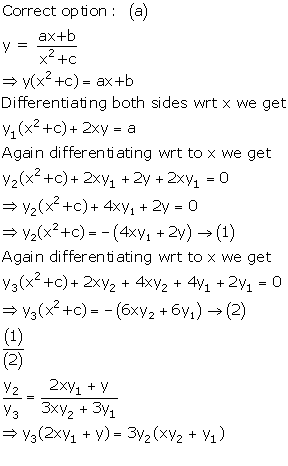
Solution 20
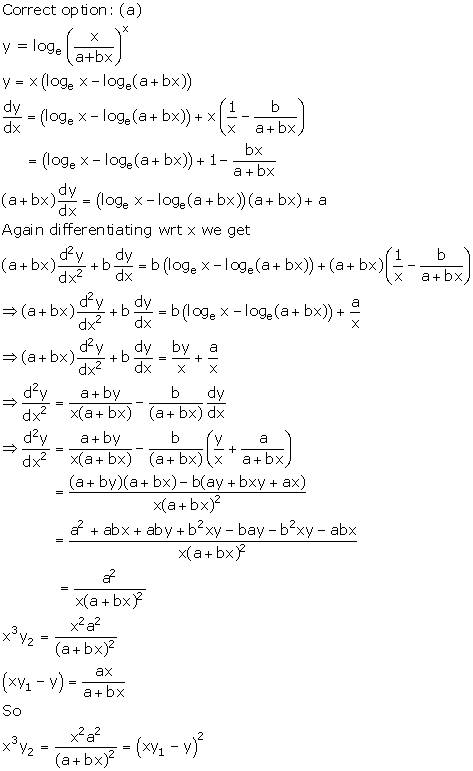
Solution 21
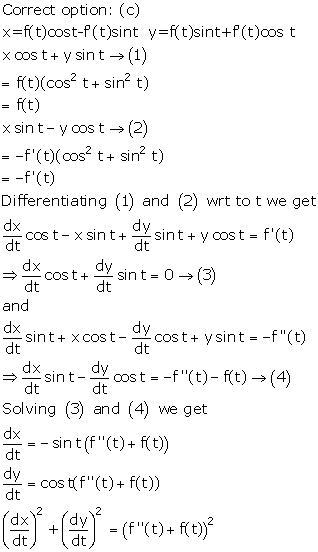
Solution 22
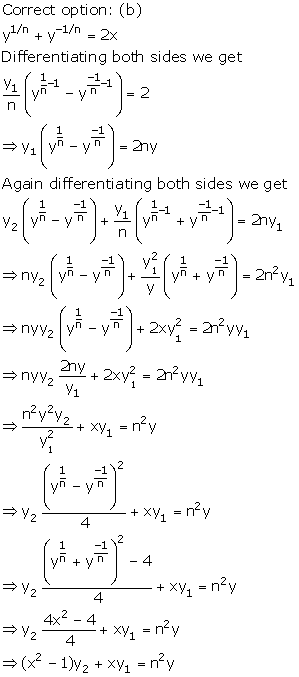
Solution 23
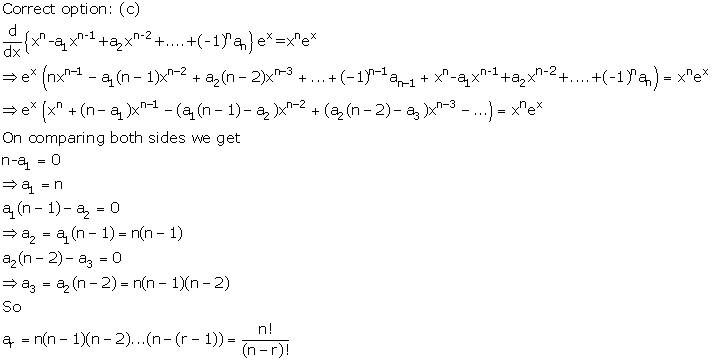
Solution 24

Solution 25

Solution 26
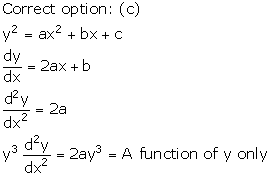
Solution 27
Given: ![]()
Differentiating the above equation w.r.t x, we get
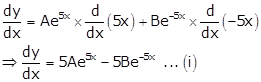
Differentiating the equation (i) w.r.t x, we get
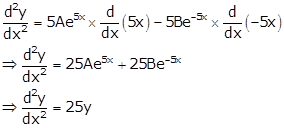
Solution 28
Given: ![]()
Differentiating the above equation w.r.t x, we get
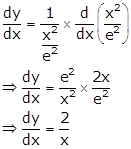
Again differentiating w.r.t x, we get
![]()
Higher Order Derivatives Exercise Ex. 12VSAQ
Solution 1

Solution 2

Solution 3
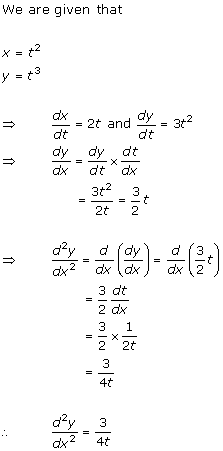
Solution 4
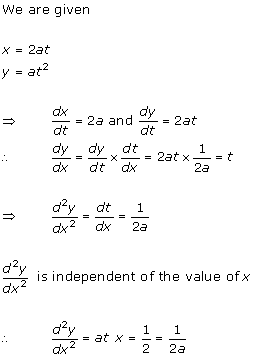
Solution 5
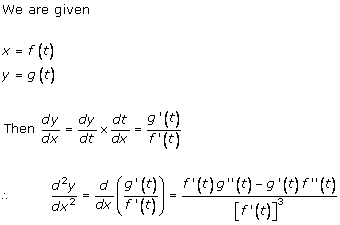
Solution 6
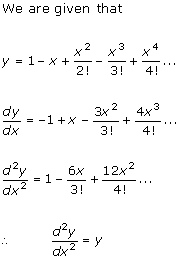
Solution 7

Solution 8

Solution 9