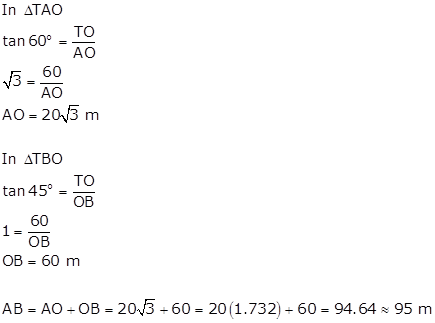Class 10 SELINA Solutions Maths Chapter 22 - Heights and Distances
Heights and Distances Exercise Ex. 22(A)
Solution 1

Let the length of the shadow of the tree be x m.
![]() Height of the tree =
Height of the tree = ![]() m
m
If ![]() is the angle of elevation of the
sun, then
is the angle of elevation of the
sun, then
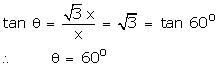
Solution 2

Let the height of the tower be h m.
Given that angle of elevation is 60o
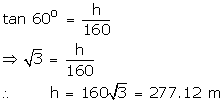
So, height of the tower is 277.12 m.
Solution 3
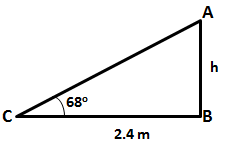
Let the height upto which the ladder reaches be h m.
Given that angle of elevation is 68o

So, the ladder reaches upto a height of 5.94 m.
Solution 4

Let one person A be at a distance x and the second person B be at a distance of y from the foot of the tower.
Given that angle of elevation of A is 30o
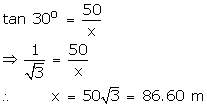
The angle of elevation of B is 38o
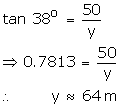
So, distance between A and B is x + y = 150.6 m
Solution 5
Let the length of the rope be x m.
Now,

So, the length of the rope is 120m.
Solution 6
Let the height of the tower be h m.
(i) Here ![]()
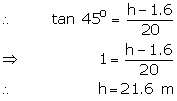
So, height of the tower is 21.6 m.
(ii) Here ![]()
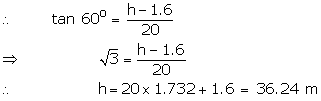
So, height of the tower is 36.24 m.
Solution 7
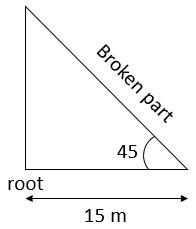
Let the height of the tree after breaking be h m.
Here ![]()
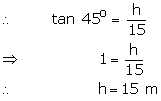
Now, length of the tree broken by the wind = ![]()
So, height of the tree before it was broken is (15 + 21.21) m = 36.21 m.
Solution 8
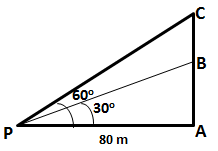
Let AB be the unfinished tower and C be the top of the tower when finished. Let P be a point 80 m from the foot A.
In ![]() BAP,
BAP,

In ![]() CAP,
CAP,

Therefore, the tower must be raised by (138.56 - 46.19)m = 92.37 m
Solution 9
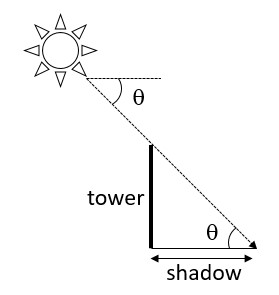
Let the length of the tower be h m.
(i) Here ![]()
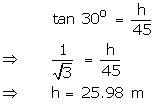
Hence the length of the tower is 25.98 m.
(ii) Let the length of the shadow be x m.
(a) Here, ![]()

Hence the length of the shadow is 25.98 m
(b) Here, ![]()

Hence the length of the shadow is 15 m.
Solution 10

Let AB be the ladder and ![]() ABP = 32o24'.
ABP = 32o24'.
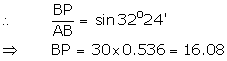
When rotated, let the ladder be AC and ![]() CAQ = 32o24'.
CAQ = 32o24'.
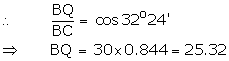
Hence, width of the road = (16.08 + 25.32) = 41.4 m
Solution 11
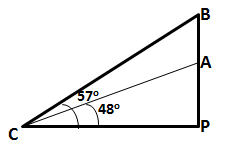
Let P be the foot of the cliff on level ground.
Then, ![]() ACP = 48o and
ACP = 48o and ![]() BCP = 57o
BCP = 57o

Hence, distance between the climbers = AB = BP - AP = 17.16 m
Solution 12
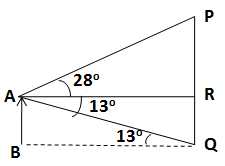
Let AB be the man and PQ be the flag-pole.
Given, AR = 9 m.
Also, ![]() PAR = 28o
and
PAR = 28o
and ![]() QAR
= 13o
QAR
= 13o

Hence, height of the pole = PR + RQ = 6.867 m
Solution 13
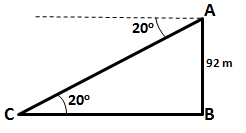
Let AB be the cliff and C be the buoy.
Given, AB = 92 m.
Also, ![]() ACB = 20o
ACB = 20o
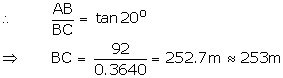
Hence, the buoy is at a distance of 253 m from the foot of the cliff.
Heights and Distances Exercise Ex. 22(B)
Solution 1

Solution 2
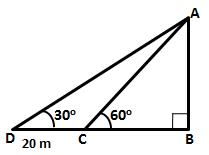
Let AB be the tree of height h m.
Let the two points be C
and D such that CD = 20 m, ![]() ADB
= 30o and
ADB
= 30o and ![]() ACB = 60o
ACB = 60o
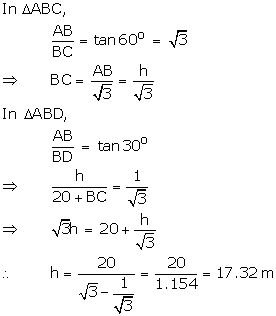
Hence, height of the tree is 17.32 m.
Solution 3

Let AB be the building of height h m.
Let the two points be C
and D such that CD = 40 m, ![]() ADB
= 30o and
ADB
= 30o and ![]() ACB = 45o
ACB = 45o
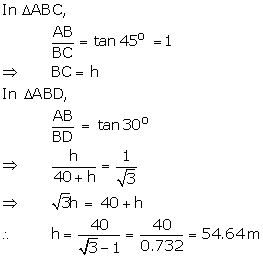
Hence, height of the building is 54.64 m.
Solution 4

Let AB be the lighthouse.
Let the two ships be C
and D such that ![]() ADB = 36o
and
ADB = 36o
and ![]() ACB = 48o
ACB = 48o
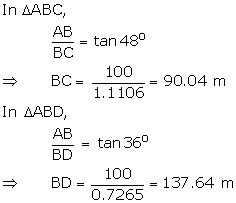
(i) If the ships are on the same side of the light house,
then distance between the two ships = BD - BC = 48 m
(ii) If the ships are on the opposite sides of the light house,
then distance between the two ships = BD + BC = 228 m
Solution 5
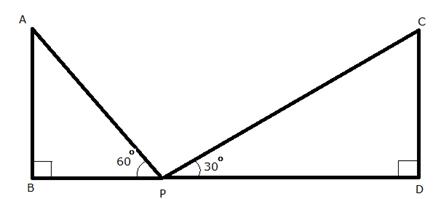
Let AB and CD be the two towers of height h m.
Let P be a point in the
roadway BD such that BD = 150 m, ![]() APB
= 60o and
APB
= 60o and ![]() CPD = 30o
CPD = 30o
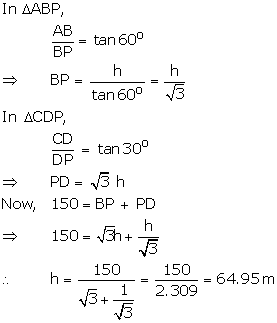
Hence, height of the pillars is 64.95 m.
The point is ![]() from the first
pillar.
from the first
pillar.
That is the position of
the point is ![]() from the
first pillar.
from the
first pillar.
The position of the point is 37.5 m from the first pillar.
Solution 6
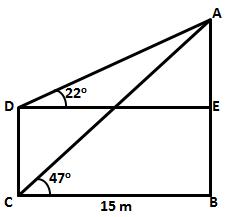

Solution 7

Let AB be the tower of height h m.
Let the two points be C
and D such that CD = 30 m, ![]() ADE
= 45o and
ADE
= 45o and ![]() ACB = 60o
ACB = 60o

Hence, height of the tower is 70.98 m
(ii)
The horizontal distance from the points of observation is BC = 40.98 m
Solution 8
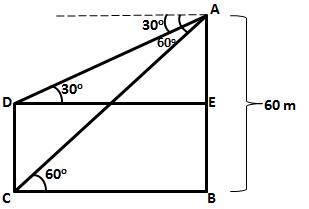
Let AB be the cliff and CD be the tower.
Here AB = 60 m, ![]() ADE = 30o
and
ADE = 30o
and ![]() ACB = 60o
ACB = 60o

Hence, height of the tower is 40 m.
Solution 9
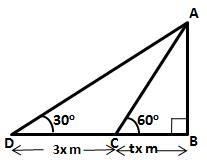
Let AB be the cliff and
C and D be the two positions of the boat such that ![]() ADE = 30o
and
ADE = 30o
and ![]() ACB = 60o
ACB = 60o
Let speed of the boat be x metre per minute and let the boat reach the shore after t minutes more.
Therefore, CD = 3x m ; BC = tx m

Hence, the boat takes an extra 1.5 minutes to reach the shore.
And, if the height of cliff is 500 m, the speed of the boat is 3.21 m/sec
Solution 10
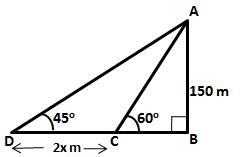
Let AB be the
lighthouse and C and D be the two positions of the boat such that AB = 150 m,
![]() ADB = 45o
and
ADB = 45o
and ![]() ACB = 60o
ACB = 60o
Let speed of the boat be x metre per minute.
Therefore, CD = 2x m ;

Hence, the speed of the boat is 0.53 m/sec
Solution 11
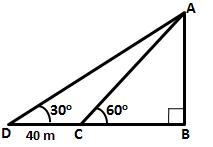
Let AB be the tree of
height 'h' m and BC be the width of the river. Let D be the point on the
opposite bank of tree such that CD = 40 m. Here ![]() ADB = 30o
and
ADB = 30o
and ![]() ACB = 60o
ACB = 60o
Let speed of the boat be x metre per minute.
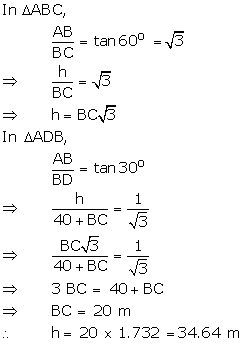
Hence, height of the tree is 34.64 m and width of the river is 20 m.
Solution 12
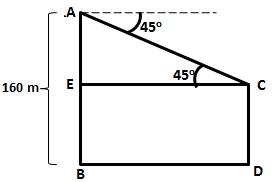
Let AB and CD be the two towers
The height of the first tower is AB = 160 m
The horizontal distance between the two towers is
BD = 75 m
And the angle of
depression of the first tower as seen from the top of the second tower is ![]() ACE = 45o.
ACE = 45o.

Hence, height of the other tower is 85 m
Solution 13
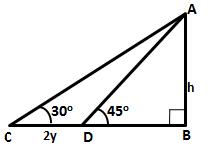
Let AB be the tower and
C and D are two points such that CD = 2y m, ![]() ADB = 45o
and
ADB = 45o
and ![]() ACB = 30o
ACB = 30o

Hence, height of the
tower is ![]() m.
m.
Solution 14

Let A be the aeroplane and B be the observer on the ground. The vertical height will be AC = 1 km = 1000 m. After 10 seconds, let the aeroplane be at point D.
Let the speed of the aeroplane be x m/sec
![]() CE = 10x
CE = 10x
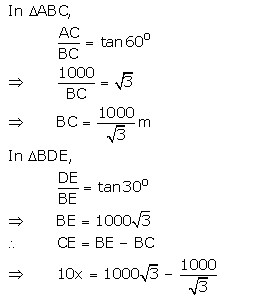

Hence, speed of the aeroplane is 415.69 km/hr
Solution 15
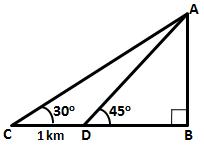
Let AB be the hill of
height 'h' km and C and D be the two consecutive stones such that CD = 1 km, ![]() ACB = 30o
and
ACB = 30o
and ![]() ADB = 45o.
ADB = 45o.

Hence, the two stones are at a distance of 1.366 km and 2.366 km from the foot of the hill.
Heights and Distances Exercise Ex. 22(C)
Solution 1

Solution 2

Solution 3

Solution 4
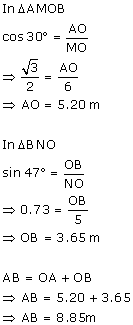
Solution 5

Given, CA = CB = 15 cm, ![]() ACB = 131o
ACB = 131o
Drop a perpendicular CP from centre C to the chord AB.
Then CP bisects ![]() ACB as well as chord AB.
ACB as well as chord AB.
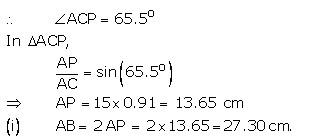
(ii) CP = AC cos (65.5o)
=15×0.415 = 6.225 cm.
Solution 6
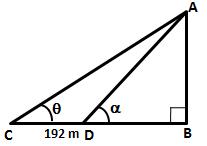
Let AB be the vertical tower and C and D be two points such that CD = 192 m. Let ![]() ACB =
ACB = ![]() and
and ![]() ADB =
ADB = ![]() .
.


Hence, the height of the tower is 180 m.
Solution 7

Let AB be the tower of height x metre, surmounted by a vertical flagstaff AD. Let C be a point on the plane such that ![]() and AD = h.
and AD = h.

Solution 8
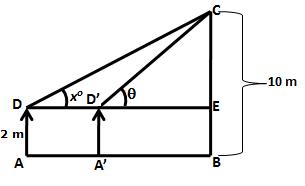
Let AD be the height of the man, AD = 2 m.

Solution 9

Let AB be the tower of height h metres.
Let C and D be two points on the level ground such that BC = b metres, BD = a metres, ![]() .
.

Solution 10
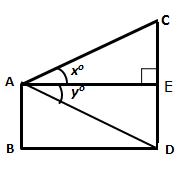

Solution 11
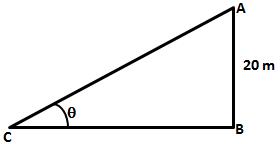
Let AB be the tower of height 20 m.
Let ![]() be the angle of elevation of the top of the tower from point C.
be the angle of elevation of the top of the tower from point C.
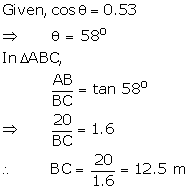
Solution 12

Let AB be the tree and AC be the width of the river. Let D be a point such that CD = 50 m. Given that ![]()

Solution 13


Solution 14
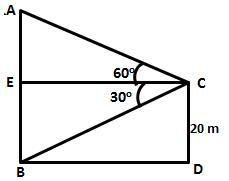
Let AB be the tower and CD be the pole.
Then ![]()

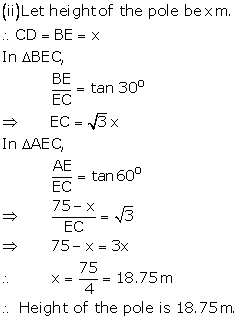
Solution 15

Let A be a point 36 m above the surface of the lake and B be the position of the bird. Let B' be the image of the bird in the water.

Solution 16
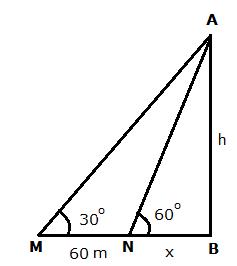
Let AB be a building and M and N are the two positions of the man which makes angles of elevation of top of building as 30o and 60o respectively.
MN = 60 m
Let AB = h and NB = x m
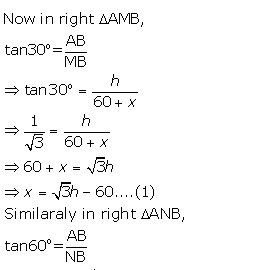

Solution 17

Let AB represent the lighthouse.
Let the two ships be at points D and C having angle of depression 30° and 40° respectively.
Let x be the distance between the two ships.

The distance between the two ships is 43 m.
Solution 18
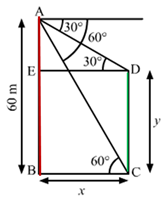

Solution 19
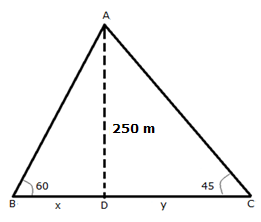
Let A be the position of the airplane and let BC be the river. Let D be the point in BC just below the airplane.
B and C be two boats on the opposite banks of the river with angles of depression 60° and 45° from A.

Solution 20
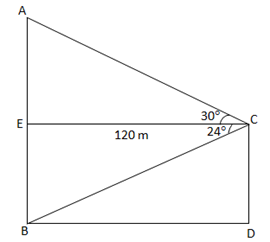

Solution 21
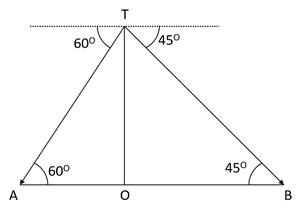
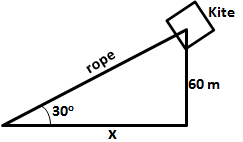
In the above figure
OT=tower = 60m
A and B are the respective positions of ship