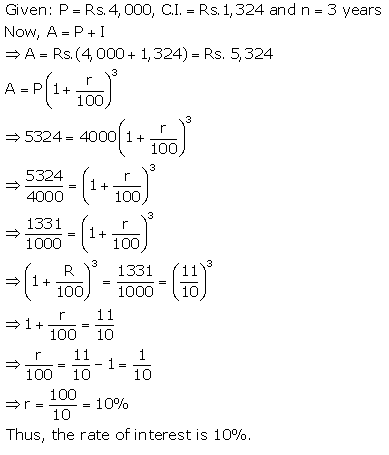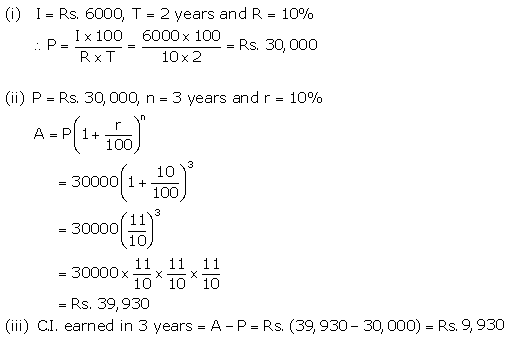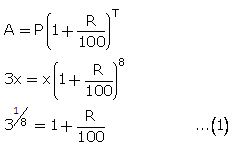Class 9 SELINA Solutions Maths Chapter 3 - Compound Interest (Using Formula)
Compound Interest (Using Formula) Exercise Ex. 3(A)
Solution 1(a)
Correct option: (i) ![]()
When the interest is compounded yearly, the formula for
finding the amount is ![]() .
.
Solution 1(b)
Correct option:
(ii) ![]()
When the rates for successive years are different then,
![]() .
.
Solution 1(c)
Correct option: (i) Rs. 3690
P = Rs. 36000, n = 2 years, r = 5%
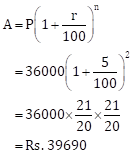
C.I. = A - P = Rs. 39690 - Rs. 36000 = Rs. 3690
Solution 1(d)
Correct option: (iii) Rs. 5000
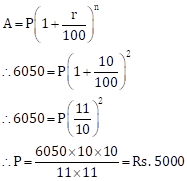
Solution 1(e)
Correct option: (iv) Rs. 5500

Solution 1(f)
Correct option: (i) 15%
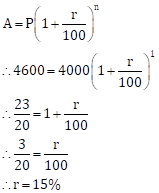
Solution 1(g)
Correct option: (ii) 15%
A = Rs. 5017.60, P = Rs. 4000. T =
2 months = ![]()
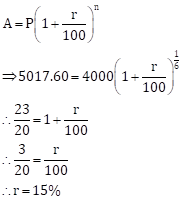
Solution 2
Given : P= Rs12,000; n=3years and r=5%
Amount= ![]() =
= ![]()
=![]()
=Rs13,891.50 Ans.
![]() C.I. =RS13,891.50 - Rs12,000
C.I. =RS13,891.50 - Rs12,000
= Rs1,891.50 Ans.
Solution 3
Given : P= Rs15,000; n=2years; r1 =8% and r2 =10%
Amount=![]() =
=![]()
=![]()
=Rs17,820 Ans.
Solution 4
Given : P=Rs6,000; n= 3years; r1= 5%; r2= 8% and r3 =10%
Amount=![]()
=![]()
=![]()
=Rs7,484.40
![]() C.I. = Rs7,484.40 - Rs6,000 = Rs1,484.40 Ans.
C.I. = Rs7,484.40 - Rs6,000 = Rs1,484.40 Ans.
Solution 5
Given : Amount= Rs5,445; n= 2years and r = 10%
![]() A=
A= ![]()
![]() 5,445=
5,445= ![]()
![]() 5,445=
5,445= ![]()
![]() P=
P=![]() =Rs4,500 Ans.
=Rs4,500 Ans.
Solution 6
Given : C.I.= Rs768.75; n= 2years and r = 5%
![]() A=
A= ![]()
![]() A=
A= ![]()
![]() A=
A=![]() =
=![]()
![]() A - P =C.I
A - P =C.I
![]()
![]() - P=Rs768.75
- P=Rs768.75
![]()
![]() =Rs768.75
=Rs768.75
![]() P=Rs
P=Rs![]() Ans.
Ans.
Solution 7
Given : C.I.= Rs1,655; n= 3years and r = 10%
![]() A=
A= ![]()
![]() A=
A= ![]()
![]() A=
A= ![]()
![]()
![]() A - P =C.I
A - P =C.I
![]()
![]() - P=Rs1,655
- P=Rs1,655
![]()
![]() =Rs1,655
=Rs1,655
![]() P=Rs
P=Rs ![]() Ans.
Ans.
Solution 8
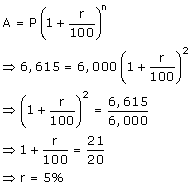
At 5% per annum the sum of Rs.6,000 amounts to Rs.6,615 in 2 years when the interest is compounded annually.
Solution 9
Given : Amount =Rs9,856; n=2years; r1 =10% and r2 =12%
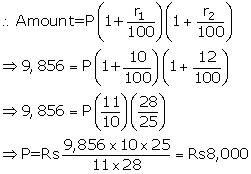
Ans.
Solution 10
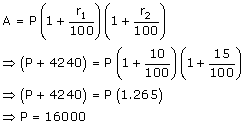
The sum is Rs.16,000
Solution 11
Let Principal = Rs y
Then Amount= Rs 1.44y
n= 2years
![]()
![]()
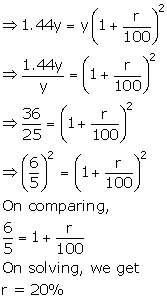
Solution 12
Solution 13
Given: P=Rs5,000; A=Rs6,272 and n= 2years
(i)
![]()
![]()
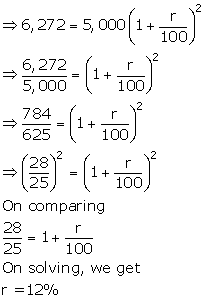
(ii) Amount at the third year
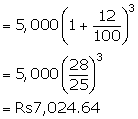
Solution 14
Given : P=Rs7,000; A=Rs9,317 and r= 10%
![]()
![]()
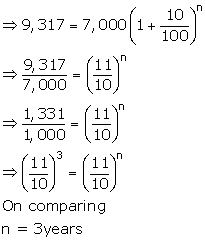
Solution 15
Given : P=Rs4,000; C.I.=Rs630.50 and r=5%
![]()
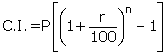
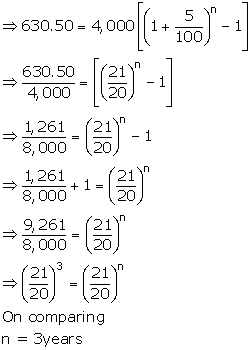
Solution 16
Let share of A = Rs y
share of B = Rs (28,730 - y)
rate of interest= 10%
According to question
Amount of A in 3years= Amount of B in 5years
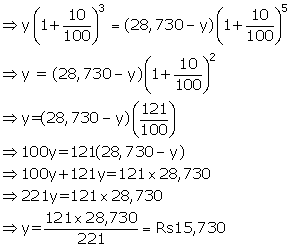
Therefore share of A=Rs15,730
Share of B=Rs28,730 - Rs 15,730=Rs13,000
Solution 17
(i)Let share of John = Rs y
share of Smith = Rs (44,200 - y)
rate of interest= 10%
According to question
Amount of John in 4years= Amount of Smith in 2years
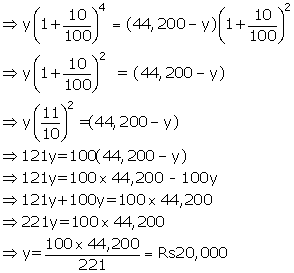
Therefore share of John=Rs20,000
Share of Smith=Rs44,200- Rs 20,000=Rs24,200
(ii)Amount that each will receive
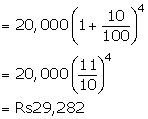
Solution 18
Solution 19

Compound Interest (Using Formula) Exercise Ex. 3(B)
Solution 1(a)
Correct option: (iii) Rs. 60

Difference between C.I. and S.I. = Rs. 1260 - Rs. 1200 = Rs. 60
Solution 1(b)
Correct option: (iv) 25%
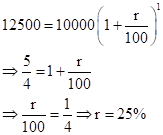
Solution 1(c)
Correct option: (ii) Rs. 7,040
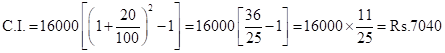
Solution 1(d)
Correct option: (ii) Rs. 6,400
![]()
Solution 1(e)
Correct option: (i) Rs. 640
Difference between C.I. and S.I. in 2 years = Rs. 7040 - Rs. 6400 = Rs. 640
Solution 2
Let principal (P) = x
R = 8%
T = 2 years
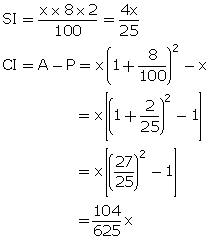
Given, CI - SI = 54.40
![]()
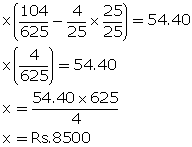
Thus, principal sum = Rs. 8500
Solution 3
Let principal = Rs. 100, R = 5% T = 2 years
For Kamal, SI = ![]()
For Anand, 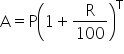
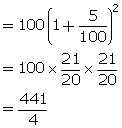
CI = 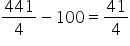
Difference of CI and SI = ![]()
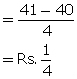
When difference is Rs. ![]() , then principal = Rs. 100
, then principal = Rs. 100
If difference is 1, principal = 100 ![]() 4
4
If difference is Rs, 15, principal = 100 ![]() 4
4 ![]() 15 = Rs. 6000
15 = Rs. 6000
For kamal, interest = ![]()
For Anand, interest = ![]()
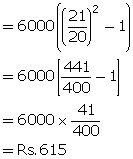
Solution 4
SI = Rs. 450
R = 4%
T = 2 years
P = ?
![]()
Now, P = 5625, R = 4%, T = 2 years
A = ![]()
![]()
CI = A - P = 6084 - 5625
= Rs. 459
Solution 5
CI = Rs. 246, R = 5%, T = 2 years
CI = A - P
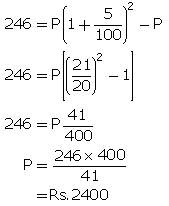
Now, P = Rs. 2400, R = 6%, T = 3 years
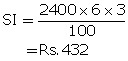
Solution 6
For 2 years, A = Rs. 19360
T = 2 years
Let P = X
![]() ...(1)
...(1)
A (for 4 years) = Rs. 23425.60
![]() ...(2)
...(2)
(2) ![]() (1)
(1)
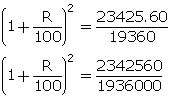
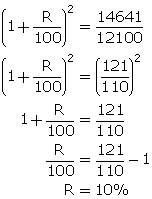
Form (1), we have
![]()
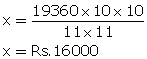
Thus, sum = Rs. 16000
Solution 7
Let principal = x, A = 3x, T = 8 years, R = ?
Case I,
Case II,
P = x, A = 27x, T = ?
![]()
![]()
From (1) and (2)
![]()

Hence, time = 24 years.
Solution 8
P = Rs. 9430
R = 5%
R = 10 years
SI = ![]()
Let sum = x
CI = 4715, T = 2 years, Rs= 5%
CI = A - P
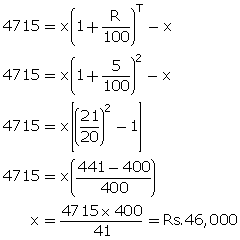
Thus principal from = Rs. 46,000
Solution 9
Let principal (P), R = 4%, T = 4 years
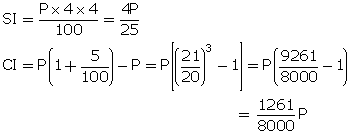
Given: SI - CI = Rs. 228

Thus, Principal = Rs. 96000
Solution 10
Let the sum (principal) = x
Given Amount = Rs. 23400, R = 10% and T = 3 years
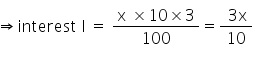
Amount = Principal + Interest
23400 = x + ![]()
x = 18000
Principle = Rs. 18000
Now,
Principal = Rs. 18000, r = 10% and n = 2 years
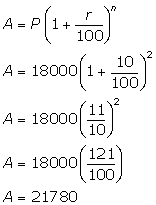
The amount of the same sum in 2 years and at 10% p.a. compound interest is Rs. 21780.
Solution 11

Compound Interest (Using Formula) Exercise Ex. 3(C)
Solution 1(a)(i)
Correct option: (2)
![]()
For n = ![]() , when interest is compounded yearly
, when interest is compounded yearly

Solution 1(a)(ii)
Correct option: (1)
![]()
For n = 1 year, when interest is compounded yearly
![]()
Solution 1(a)(iii)
Correct option: (4)
![]()
For n = ![]() , when interest is compounded yearly
, when interest is compounded yearly
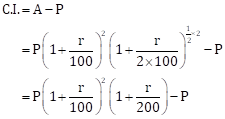
Solution 1(b)(i)
Correct option: (1)
![]()
For n = 1 year, when interest is compounded half-yearly
![]()
Solution 1(b)(ii)
Correct option: (2)
![]()
For
n = ![]() , when interest is compounded half-yearly
, when interest is compounded half-yearly
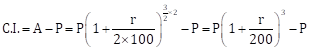
Solution 1(b)(iii)
Correct option: (3)
![]()
For n = 2 years, when interest is compounded half-yearly
![]()
Solution 1(c)
Correct option: (i) 42%
P = Rs. 6000, C.I. = Rs. 1260, n = 6 months
A = P + C.I. = Rs. 6000 + Rs. 1260 = Rs. 7260
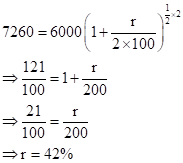
Solution 1(d)(i)
Correct option: (i) Rs. 1,200
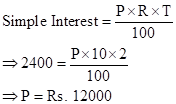
Now, C.I. for 1st year,
![]()
Solution 1(d)(ii)
Correct option: (i) Rs. 1,320
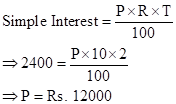
C.I. for 1st year,
![]()
C.I. for 2 years,
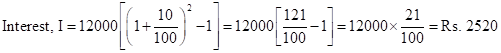
Therefore, C,.I. for 2nd year = Rs. 2520 - Rs. 1200 = Rs. 1320
Solution 1(d)(iii)
Correct option: (i) Rs. 12,000
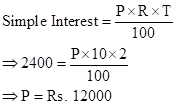
Solution 1(d)(iv)
Correct option: (i) Rs. 14,520
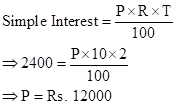
The amount in 2 years, at compound interest,
![]()
Solution 2
Given: P=Rs7,400; r=5% p.a. and n= 1year
Since the interest is compounded half-yearly,
Then ![]()
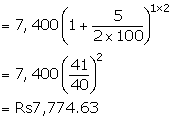
Solution 3
When interest is compounded yearly
Given: P = Rs. 10,000; n = 18 months =![]() year and r = 10% p.a.
year and r = 10% p.a.
For 1 year
![]()
![]()
![]()
![]()
For 1/2 year
P = Rs. 11,000; n = 1/2 year and r = 10%
![]()
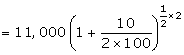
![]()
![]()
![]() C.I. = Rs. 11,550 - Rs. 10,000 = Rs. 1,550
C.I. = Rs. 11,550 - Rs. 10,000 = Rs. 1,550
When interest is compounded half-yearly
P = Rs. 10,000; n = ![]() year and r = 10% p.a.
year and r = 10% p.a.
![]()
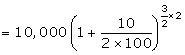
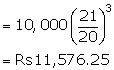
![]() C.I. = Rs. 11,576.25 - Rs. 10,000 = Rs. 1,576.25
C.I. = Rs. 11,576.25 - Rs. 10,000 = Rs. 1,576.25
![]() Difference between both C.I. = Rs. 1,576.25 - Rs.1,550
Difference between both C.I. = Rs. 1,576.25 - Rs.1,550
= Rs. 26.25
Solution 4
For the first 2 years,
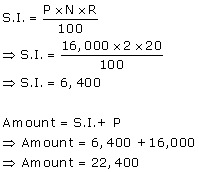
Amount in the account at the end of the two years is Rs. 22,400.
For the remaining one year,
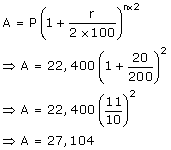
The total amount to be paid at the end of the three years is Rs. 27,104.
Solution 5
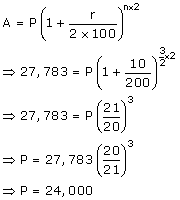
The sum of Rs.24,000 amount Rs.27,783 in one and a half years at 10% per annum compounded half yearly.
Solution 6
(i) For Ashok (interest is compounded yearly)
Let P = Rs. y; n = 18 months =![]() year and r = 20% p.a.
year and r = 20% p.a.
For 1 year
![]()
![]()
![]()
For 1/2 year
P![]() ; n = ½ year and r = 20% p.a.
; n = ½ year and r = 20% p.a.
![]()
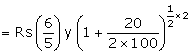
![]()
(ii) For Geeta (interest is compounded half-yearly)
P = Rs. y; n = ![]() year and r = 20% p.a.
year and r = 20% p.a.
![]()

![]()
![]()
According to question
![]()
![]()
![]()
![]()
![]() Money invested by each person = Rs. 3,000
Money invested by each person = Rs. 3,000
Solution 7
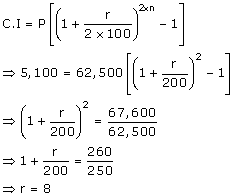
The rate of interest is 8%.
Solution 8
Given: P = Rs. 1,500; C.I. = Rs. 496.50 and r = 20%
Since interest is compounded semi-annually
Then
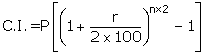
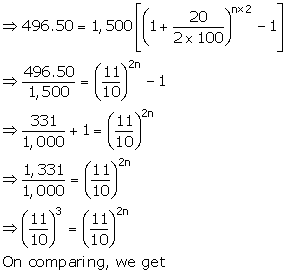
![]()
Solution 9
Given: P = Rs. 3,500; r = 6% and n= 3years
Since interest is being compounded half-yearly
Then


Solution 10
Given: P = Rs. 12,000; n= ![]() years and r = 10%
years and r = 10%
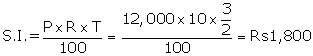
To calculate C.I.
For 1 year
P = Rs. 12,000; n = 1 year and r = 10%
![]()
For next 1/2 year
P = Rs. 13,200; n = 1/2 year and r = 10%
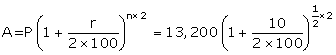
![]()
![]()
![]() C.I. = Rs. 13,860 - Rs. 12,000 = Rs. 1,860
C.I. = Rs. 13,860 - Rs. 12,000 = Rs. 1,860
![]() Difference between C.I. and S.I
Difference between C.I. and S.I
= Rs. 1,860 - Rs. 1,800 = Rs. 60
Solution 11
Given: P = Rs. 12,000; n = ![]() years and r = 10%
years and r = 10%
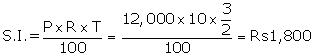
To calculate C.I.(compounded half-yearly)
P = Rs. 12,000; n =![]() and r = 10%
and r = 10%
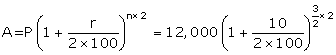
![]()
![]()
![]() C.I. = Rs. 13,891.50 - Rs. 12,000 = Rs. 1,891.50
C.I. = Rs. 13,891.50 - Rs. 12,000 = Rs. 1,891.50
![]() Difference between C.I. and S.I
Difference between C.I. and S.I
= Rs. 1,891.50 - Rs. 1,800 = Rs. 91.50
Compound Interest (Using Formula) Exercise Ex. 3(D)
Solution 1(a)
Correct option:
(iii) ![]()
When the present population (P) of a certain locality
increases by r% per year, the population in n years will be Initial
population ×![]()
![]()
Solution 1(b)
Correct option:
(ii) ![]()
In first year, the population is decreased by 10% and in the next year, the population is increased by 15%.
Therefore, the population at the end of two years = ![]()
Solution 1(c)
Correct option:
(ii) ![]()
When the cost of a machine decreases by r% per year, the
cost of machine in 3 years = ![]()
Solution 1(d)
Correct option:
(iii) ![]()
For first 2 years, r = x%
For next 3 years, r = y%
Therefore, amount after 5 years = ![]()
Solution 1(e)
Correct option:
(iii) ![]()
Initial cost of machine = Rs. x
For first 2 years, cost increases by 20% and then decreases by 25% in the next 2 years.
Therefore, the cost of machine

Solution 2
Cost of machine in 2008 = Rs. 44,000
Depreciation rate = 12%
(i) ![]() Cost of machine at the end of 2009
Cost of machine at the end of 2009
(ii) Cost of machine at the beginning of 2007(P)
Solution 3
Let x be the value of the article.
The value of an article decreases for two years at the rate of 10% per year.
The value of the article at the end of the 1st year is
x - 10% of x = 0.90x
The value of the article at the end of the 2nd year is
0.90x - 10% of (0.90x) = 0.81x
The value of the article increases in the 3rd year by 10%.
The value of the article at the end of 3rd year is
0.81x + 10% of (0.81x) = 0.891x
The value of the article at the end of 3 years is Rs.40,095.
![]()
The original value of the article is Rs. 45,000.
Solution 4
Population in 2009 (P) = 64,000
Let after n years its population be 74,088 (A)
Growth rate= 5% per annum
![]()
![]()
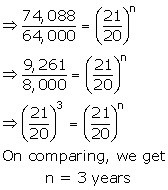
Solution 5
Let the population in the beginning of 1998 = P
The population at the end of 1999 = 2,85,120 (A)
r1 = - 12% and r2 = +8%
![]()
![]()
![]()
![]()
Solution 6
Let sum of money be Rs. P and rate of interest = r%
Money after 1 year = Rs. 16,500
Money after 3 years = Rs. 19,965
For 1 year
![]()
![]()
For 3 years
![]()
![]()
Divide eqn (2) by eqn (1)
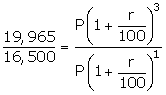
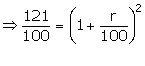
![]()
On comparing, we get
![]()
![]() r= 10%
r= 10%
Put value of r in eqn (1)
![]()
![]()
Solution 7
Given: P = Rs. 7,500 and Time (n)= 2 years
Let rate of interest = y%
![]()
![]()
Given: C.I. - S.I. = Rs. 12
![]()
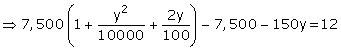
![]()
![]()
![]()
Solution 8
Let Principal be Rs. y and rate = r%
According to 1st condition
Amount in 10 years = Rs. 3y
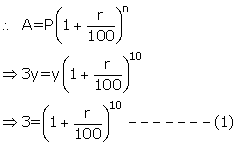
According to 2nd condition
Let after n years amount will be Rs. 27y
Solution 9
At the end of the two years the amount is
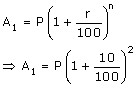
Mr. Sharma paid Rs.19,360 at the end of the second year.
So for the third year the principal is A1 - 19,360.
Also he cleared the debt by paying Rs.31,944 at the end of the third year.
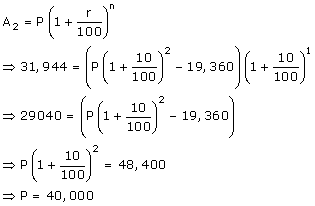
Mr. Sharma borrowed Rs.40,000.
Solution 10
Let sum of money be Rs. y
To calculate S.I.
![]()
To calculate C.I. (compounded half-yearly)
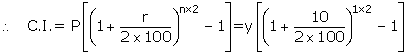
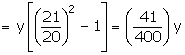

Solution 11
Let Rs.x and Rs.y be the money invested by Pramod and Rohit respectively such that they will get the same sum on attaining the age of 25 years.
Pramod will attain the age of 25 years after 25 - 16 = 9 years
Rohit will attain the age of 25 years after 25 -18 = 7 years
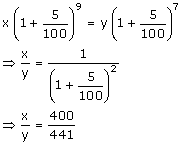
Pramod and Rohit should invest in 400:441 ratio respectively such that they will get the same sum on attaining the age of 25 years.
Compound Interest (Using Formula) Exercise Test Yourself
Solution 1
1st case
Given: S.I. = Rs 450;Time= 2 years and Rate = 4%
![]()
2nd case(compounded half-yearly)
P = Rs.5,625;n= 1 year and r = 4%
![]()
![]()
![]()
Solution 2
![]()
For 2years
![]()
For ½ year
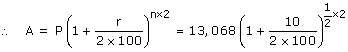
![]()
![]() C.I. = A - P = Rs.13,721 - Rs.10,800 = Rs.2,921
C.I. = A - P = Rs.13,721 - Rs.10,800 = Rs.2,921
Solution 3
(i) Present value of machine(P) = Rs.97,200
Depreciation rate = 10%
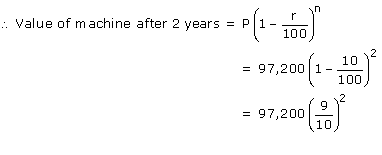
=Rs.78732
(ii) Present value of machine(A) = Rs.97,200
Depreciation rate = 10% and time = 2 years
To calculate the cost 2 years ago
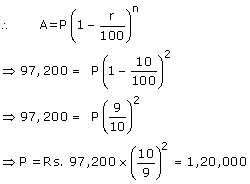
Solution 4
Let the sum of money lent by both Rs.y
For Anuj
P = Rs.y ;rate = 8% and time = 2 years
![]()
For Rajesh
P = Rs.y ;rate = 8% and time = 2 years
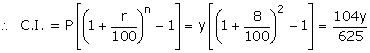
Given : C.I. - S.I. = Rs.64
![]()
![]()
![]()
![]()
Solution 5
Given: Principal = Rs.4,715;time = 5 years and rate= 5% p.a.
![]()
Then C.I. = Rs.1,178.75 x 4 = Rs.4,715
Time = 2 years and rate = 5%
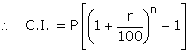
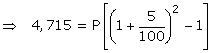
![]()
![]()
Solution 6
Given: C.I. for the 2nd year = Rs.4,950 and rate = 15%
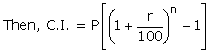
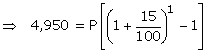
![]()
![]()
![]()
Then amount at the end of 2nd year= Rs.33,000
For first 2years
A = Rs.33,000; r1 =10%
![]()
![]()
![]()
![]()
The sum invested is Rs.30,000.
Solution 7
Let the sum of money be Rs. y
and rate = 10% p.a. compounded half yearly
For first 6 months

For first 12 months
![]()
Given: The difference between the above amounts = Rs. 189
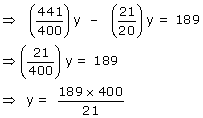
y = Rs. 3600
Solution 8
P = Rs.86,000;time = 2 years and rate = 5% p.a.
To calculate S.I.
![]()
To calculate C.I.
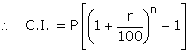
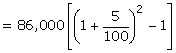
![]()
Profit = C.I. - S.I. = Rs.8,815 - Rs.8,600 = Rs.215
Solution 9
Let Rs.x be the sum of money.
Rate = 5 % p.a. Simple interest = Rs.1,200, n = 3years.
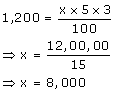
The amount due and the compound interest on this sum of money at the same rate and after 2 years.
P = Rs.8,000;rate = 5% p.a., n = 3 years

The amount due after 2 years is Rs.8,820 and the compound interest is Rs.820.
Solution 10
Let x% be the rate of interest.
P = Rs.6,000, n = 2 years, A = Rs.6,720
(a) For the first year,
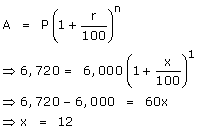
The rate of interest is x% = 12%.
(b) The amount at the end of the second year,.
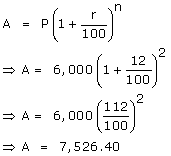
The amount at the end of the second year = Rs. 7,526.40