Class 9 NCERT Solutions Maths Chapter 9 - Circles
Ex. 9.1
Ex. 9.2
Ex. 9.3
Circles Exercise Ex. 9.1
Solution 1
A circle is a collection of points which are equidistant from a fix point. This fix point is called as the centre of circle and this equal distance is called as radius of circle. And thus shape of a circle depends on the radius of the circle.
So, if we try to superimpose two circles of equal radius, one each other both circles will cover each other.
So, two circles are congruent if they have equal radius.
So, if we try to superimpose two circles of equal radius, one each other both circles will cover each other.
So, two circles are congruent if they have equal radius.
Now consider two congruent circles having centre O and O' and two chords AB and CD of equal lengths
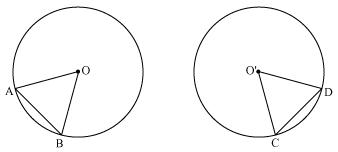
Now in  AOB and
AOB and  CO'D
CO'D
AB = CD (chords of same length)
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
 AOB
AOB 
 CO'D (SSS congruence rule)
CO'D (SSS congruence rule)
AB = CD (chords of same length)
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
Hence equal chords of congruent circles subtend equal angles at their centres.
Solution 2
Let us consider two congruent circles (circles of same radius) with centres as O and O'.
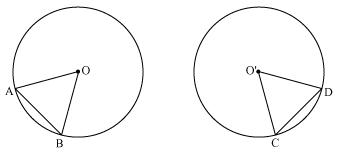
In 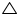 AOB and
AOB and 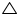 CO'D
CO'D
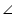 AOB =
AOB = 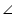 CO'D (given)
CO'D (given)
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
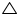 AOB
AOB 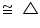 CO'D (SSS congruence rule)
CO'D (SSS congruence rule)
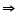 AB = CD (by CPCT)
AB = CD (by CPCT)
Hence, if chords of congruent circles subtend equal angles at their centres then chords are equal.
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
Hence, if chords of congruent circles subtend equal angles at their centres then chords are equal.
Circles Exercise Ex. 9.2
Solution 1
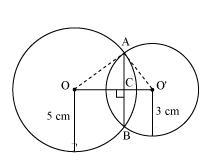
Let radius of circle centered at O and O' be 5 cm and 3 cm respectively.
OA = OB = 5 cm
O'A = O'B = 3 cm
OO' will be the perpendicular bisector of chord AB.
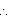 AC = CB
AC = CB
OA = OB = 5 cm
O'A = O'B = 3 cm
OO' will be the perpendicular bisector of chord AB.
Given that OO' = 4 cm
Let OC be x. so, O'C will be 4 - x
In
OA2 = AC2 + OC2
In
O'A2 = AC2 + O'C2
From equations (1) and (2), we have
25 - x2 = - x2 - 7 + 8x
8x = 32
x = 4
So, the common chord will pass through the centre of smaller circle i.e. O'. and hence it will be diameter of smaller circle.
Now, AC2 = 25 - x2 = 25 - 42 = 25 - 16 = 9
 AC = 3 m
AC = 3 m
The length of the common chord AB = 2 AC = (2
Solution 2
Let PQ and RS are two equal chords of a given circle and there are intersecting each other at point T.
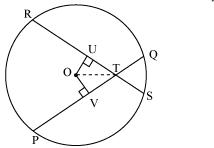
Draw perpendiculars OV and OU on these chords.
In OVT and
OVT and  OUT
OUT
OV = OU (Equal chords of a circle are equidistant from the centre)
 OVT =
OVT = 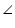 OUT (Each 90o)
OUT (Each 90o)
OT = OT (common)
In
OV = OU (Equal chords of a circle are equidistant from the centre)
OT = OT (common)
It is given that
PQ = RS ... ... ... ... (2)
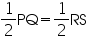
On adding equations (1) and (3), we have
PV + VT = RU + UT
On subtracting equation (4) from equation (2), we have
PQ - PT = RS - RT
Equations (4) and (5) shows that the corresponding segments of
chords PQ and RS are congruent to each other.
Solution 3
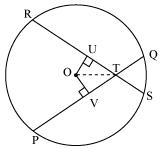
Let PQ and RS are two equal chords of a given circle and there are intersecting each other at point T.
Draw perpendiculars OV and OU on these chords.
In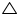 OVT and
OVT and 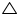 OUT
OUT
OV = OU (Equal chords of a circle are equidistant from the centre)
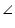 OVT =
OVT = 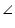 OUT (Each 90o)
OUT (Each 90o)
OT = OT (common)
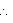
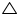 OVT
OVT 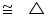 OUT (RHS congruence rule)
OUT (RHS congruence rule)
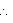
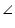 OTV =
OTV = 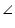 OTU (by CPCT)
OTU (by CPCT)
Draw perpendiculars OV and OU on these chords.
In
OV = OU (Equal chords of a circle are equidistant from the centre)
OT = OT (common)
Hence, the line joining the point of intersection to the centre makes equal angles with the chords.
Solution 4
Let us draw a perpendicular OM on line AD.

Here, BC is chord of smaller circle and AD is chord of bigger circle.
We know that the perpendicular drawn from centre of circle bisects the chord.
And AM = MD ... (2)
Subtracting equations (2) from (1), we have
AM - BM = MD - MC
Solution 5
Draw perpendiculars OA and OB on RS and SM respectively.
Let R, S and M be the position of Reshma, Salma and Mandip respectively.
Let R, S and M be the position of Reshma, Salma and Mandip respectively.
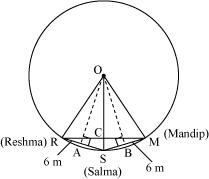
AR = AS = 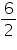 = 3cm
= 3cm
OR = OS = OM = 5 m (radii of circle)
In OAR
OA2 + AR2 = OR2
OA2 + (3 m)2 = (5 m)2
OA2 = (25 - 9) m2 = 16 m2
OA = 4 m
We know that in an isosceles triangle altitude divides the base, so in RSM
RSM
 RCS will be of 90o and RC = CM
RCS will be of 90o and RC = CM
Area of ORS =
ORS = 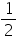
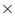 OA
OA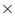 RS
RS
In OAR
OA2 + AR2 = OR2
OA2 + (3 m)2 = (5 m)2
OA2 = (25 - 9) m2 = 16 m2
OA = 4 m
We know that in an isosceles triangle altitude divides the base, so in
Area of
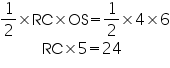
RC = 4.8
RM = 2RC = 2(4.8)= 9.6
So, distance between Reshma and Mandip is 9.6 m.
Solution 6
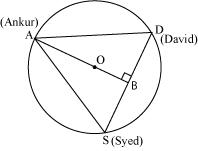
Given that AS = SD = DA
So, ASD is a equilateral triangle
OA (radius) = 20 m.
Medians of equilateral triangle pass through the circum centre (O) of the equilateral triangle ABC.
We also know that median intersect each other at the 2: 1. As AB is the median of equilateral triangle ABC, we can write
So, ASD is a equilateral triangle
OA (radius) = 20 m.
Medians of equilateral triangle pass through the circum centre (O) of the equilateral triangle ABC.
We also know that median intersect each other at the 2: 1. As AB is the median of equilateral triangle ABC, we can write
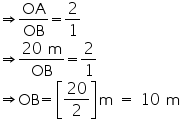
In
AD2 = AB2 + BD2
AD2 = (30)2 +
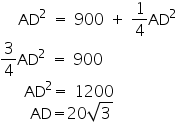
So, length of string of each phone will be
Circles Exercise Ex. 9.3
Solution 1
We may observe that
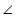 AOC =
AOC = 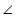 AOB +
AOB + 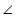 BOC
BOC
= 60o + 30o
= 90o
We know that angle subtended by an arc at centre is double the angle subtended by it any point on the remaining part of the circle.
= 60o + 30o
= 90o
We know that angle subtended by an arc at centre is double the angle subtended by it any point on the remaining part of the circle.
Solution 2
In  OAB
OAB
AB = OA = OB = radius
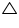 OAB is an equilateral triangle.
OAB is an equilateral triangle.
AB = OA = OB = radius
So, each interior angle of this triangle will be of 60o
Now, 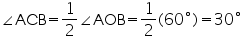
In cyclic quadrilateral ACBD
 ACB +
ACB + 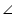 ADB = 180o (Opposite angle in cyclic quadrilateral)
ADB = 180o (Opposite angle in cyclic quadrilateral)
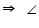 ADB = 180o - 30o = 150o
ADB = 180o - 30o = 150o
So, angle subtended by this chord at a point on major arc and minor arc are 30o and 150o respectively.
So, angle subtended by this chord at a point on major arc and minor arc are 30o and 150o respectively.
Solution 3
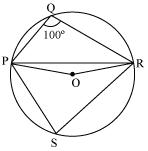
Consider PR as a chord of circle.
Take any point S on major arc of circle.
Now PQRS is a cyclic quadrilateral.
We know that angle subtended by an arc at centre is double the angle subtended by it any point on the remaining part of the circle.
In 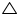 POR
POR
OP = OR (radii of same circle)
OP = OR (radii of same circle)
2 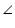 OPR + 160o= 180o
OPR + 160o= 180o
2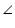 OPR = 180o - 160o = 20o
OPR = 180o - 160o = 20o
2
Solution 4
In 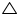 ABC
ABC
Solution 5
In 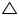 CDE
CDE
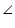 CDE +
CDE + 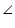 DCE =
DCE = 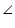 CEB (Exterior angle)
CEB (Exterior angle)
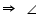 CDE + 20o = 130o
CDE + 20o = 130o
But
Solution 6
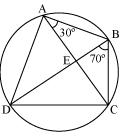
For chord CD
In
AB = BC (given)
 BCA =
BCA =  CAB (Angles opposite to equal sides of a triangle)
CAB (Angles opposite to equal sides of a triangle)
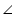 BCA = 30o
BCA = 30o
We have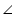 BCD = 80o
BCD = 80o
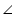 BCA +
BCA + 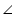 ACD = 80o
ACD = 80o
30o +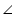 ACD = 80o
ACD = 80o
We have
30o +
Solution 7
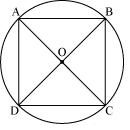
Let ABCD a cyclic quadrilateral having diagonals as BD and AC intersecting each other at point O.
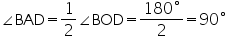 (Consider BD as a chord)
(Consider BD as a chord)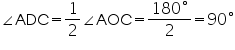 (Considering AC as a chord)
(Considering AC as a chord)90o +
Here, each interior angle of cyclic quadrilateral is of 90o. Hence it is a rectangle.
Solution 8
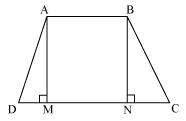
Consider a trapezium ABCD with AB | |CD and BC = AD Draw AM  CD and BN
CD and BN  CD
CD
In AMD and
AMD and  BNC
BNC
AD = BC (Given)
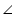 AMD =
AMD = 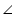 BNC (By construction each is 90o)
BNC (By construction each is 90o)
AM = BM (Perpendicular distance between two parallel lines is same)
 AMD
AMD  BNC (RHS congruence rule)
BNC (RHS congruence rule)
In
AD = BC (Given)
AM = BM (Perpendicular distance between two parallel lines is same)
This equation shows that the opposite angles are supplementary.
So, ABCD is a cyclic quadrilateral.
Solution 9
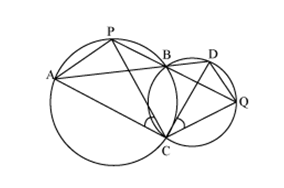
Join chords AP and DQ
For chord AP
 PBA =
PBA = 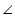 ACP (Angles in same segment) ... (1)
ACP (Angles in same segment) ... (1)
For chord DQ
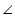 DBQ =
DBQ = 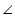 QCD (Angles in same segment) ... (2)
QCD (Angles in same segment) ... (2)
ABD and PBQ are line segments intersecting at B.
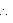
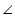 PBA =
PBA = 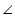 DBQ (Vertically opposite angles) ... (3)
DBQ (Vertically opposite angles) ... (3)
From equations (1), (2) and (3), we have
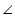 ACP =
ACP = 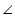 QCD
QCD
For chord AP
For chord DQ
ABD and PBQ are line segments intersecting at B.
From equations (1), (2) and (3), we have
Solution 10
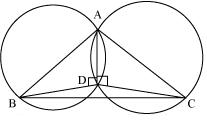
Consider a  ABC
ABC
Two circles are drawn while taking AB and AC as diameter.
Let they intersect each other at D and let D does not lie on BC.
Join AD
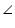 ADB = 90o (Angle subtend by semicircle)
ADB = 90o (Angle subtend by semicircle)
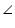 ADC = 90o (Angle subtend by semicircle)
ADC = 90o (Angle subtend by semicircle)
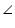 BDC =
BDC = 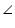 ADB +
ADB + 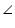 ADC = 90o + 90o = 180o
ADC = 90o + 90o = 180o
Hence BDC is straight line and our assumption was wrong.
Thus, Point D lies on third side BC of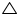 ABC
ABC
Two circles are drawn while taking AB and AC as diameter.
Let they intersect each other at D and let D does not lie on BC.
Join AD
Hence BDC is straight line and our assumption was wrong.
Thus, Point D lies on third side BC of
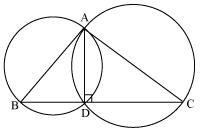
Solution 11
In  ABC
ABC
In
Adding equations (1) and (2), we have
But it is given that
From equations (3) and (4), we can see that quadrilateral ABCD is having sum of measures of opposite angles as 180o.
So, it is a cyclic quadrilateral.
Consider chord CD.
Now,
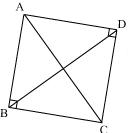
Solution 12
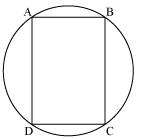
Let ABCD be a cyclic parallelogram.
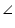 A +
A + 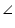 C = 180o (Opposite angle of cyclic quadrilateral) ... (1)
C = 180o (Opposite angle of cyclic quadrilateral) ... (1)
We know that opposite angles of a parallelogram are equal
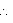
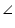 A =
A = 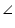 C and
C and 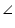 B =
B = 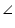 D
D
From equation (1)
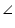 A +
A + 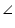 C = 180o
C = 180o
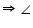 A +
A + 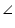 A = 180o
A = 180o
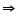 2
2 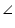 A = 180o
A = 180o
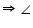 A = 90o
A = 90o
Parallelogram ABCD is having its one of interior angles as 90o, so, it is a rectangle.
We know that opposite angles of a parallelogram are equal
From equation (1)
Parallelogram ABCD is having its one of interior angles as 90o, so, it is a rectangle.

