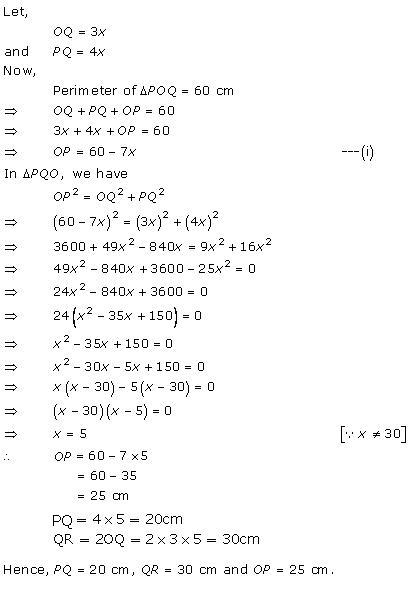Class 10 RD SHARMA Solutions Maths Chapter 8 - Circles
The Central Board of Secondary Education, or CBSE, is a national educational board in India. It sets the curriculum and syllabus and conducts examinations for all affiliated schools. The Board aims to provide a syllabus that lays out a structured framework for teachers and students and thus offers a systematic and comprehensive approach to learning.
The CBSE Class 10 Maths syllabus outlines the specific topics, subtopics, and learning objectives students must cover. It provides a well-rounded mathematical education through chapters such as Real Numbers, Pair of Linear Equations in Two Variables, Quadratic Equations, Arithmetic Progressions, Triangles, Introduction to Trigonometry, Circles, etc. Thus it helps students develop mathematical understanding, problem-solving skills, and logical reasoning abilities.
Circles is an important chapter in Class 10 as it focuses on understanding the properties and characteristics of a circle. It deals with the various elements of the shape, like its radius, diameter, chord, and arc. Studying this chapter lays the foundation for advanced concepts in geometry, which might come into use in various fields like architecture, engineering, and physics.
RD Sharma Solutions covers in detail all the topics and concepts included in the CBSE Class 10 Mathematics syllabus. They provide step-by-step solutions to every question covered in the textbook and ensure that the students grasp the underlying principles and techniques. With its simple, crisp and easy-to-understand language, it focuses on simplifying complex concepts so that students can understand and retain them better. The solutions also consist of detailed construction problems related to circles and guide students through the step-by-step construction using a compass and straightedge.
At TopperLearning, we believe in making online education more affordable and accessible to all. Therefore, we provide completely free access to all RD Sharma solutions from class 9 to class 12 so that students can effectively prepare and secure high marks in exams. Students can revise concepts and design notes from these solutions. We also offer video lessons, sample papers, previous years’ question papers, revision notes and an Ask a Doubt app that lets students search for an answer by text or voice. Thus, through TopperLearning, anyone can study from anywhere!
Circles Exercise Ex. 8.1
Solution 1
Fill in the blanks:
(i) The common point of a tangent and the circle is called point of contact .
(ii) A circle may have two parallel tangents.
(iii) A tangent to a circle intersects it in one point(s).
(iv) A line intesecting a circle in two points is called a secant .
(v) The angle between tangent at a point on a circle and the radius through the point is 90o .
Solution 2
Solution 3

Solution 4

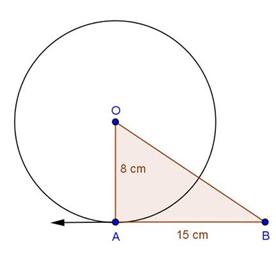
Circles Exercise Ex. 8.2
Solution 1

Solution 2

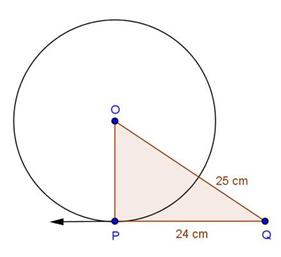
Solution 3


Solution 4
Solution 5
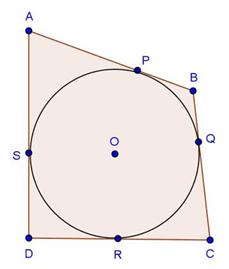

Solution 6
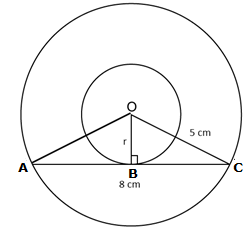

Solution 7
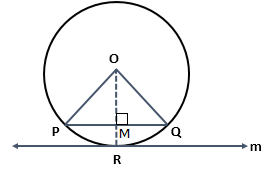

Solution 8
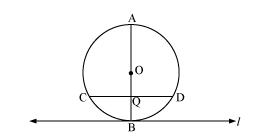

Solution 9

Solution 10

Solution 11


Solution 12

Solution 13


Solution 14

Solution 15
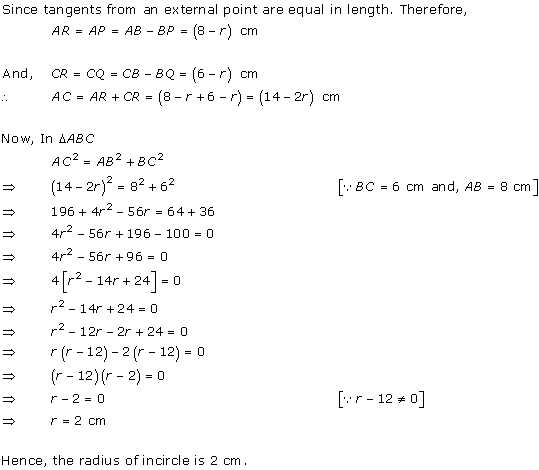
Solution 16

Solution 17

Solution 18


Solution 19


Solution 20

Solution 21
Solution 22

Solution 23
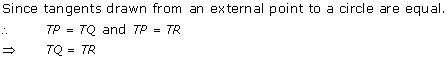
Solution 24
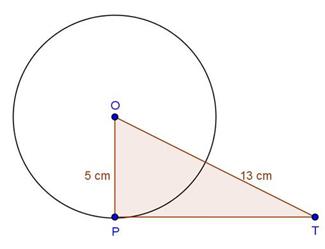
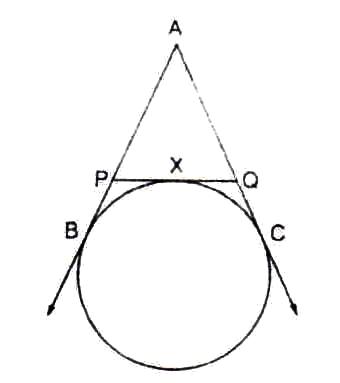
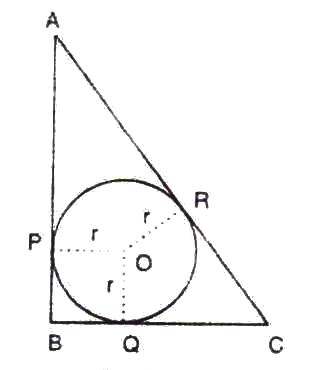
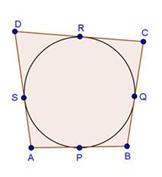
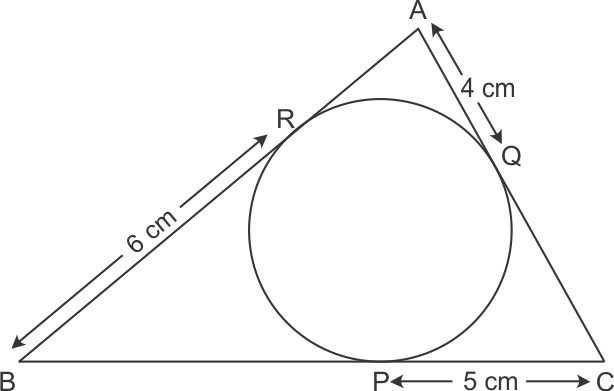
AP = AQ , BP = PR and CR = CQ (tangents from an external point)
Perimeter of ∆ABC = AB + BR + RC + CA
= AB + BP + CQ + CA
= AP + AQ
= 2AP
∆APO is a right-angled triangle. AO2 = AP2 + PO2
132 = AP2 + 52
AP2 = 144
AP = 12
∴ Perimeter of ∆ABC = 24 cm
Solution 25

Solution 26
Solution 27

Solution 28

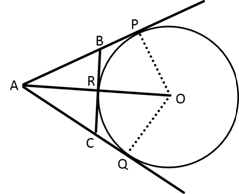
Solution 29

Solution 30
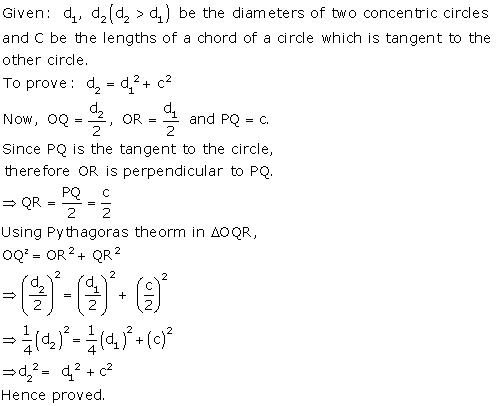
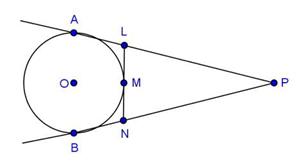
Solution 31
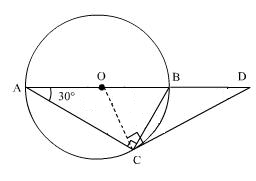
Since RS is drawn parallel to the tangent PQ,
∠SRQ = ∠PQR
Also, PQ = PR
⇒ ∠PQR = ∠PRQ
In ∆PQR,
∠PQR + ∠PRQ + ∠QPR = 180°
⇒∠PQR + ∠PQR + 30° = 180°
⇒2∠PQR = 150°
⇒∠PQR = 75°
⇒∠SRQ =∠PQR = 75° (alternate angles)
Also, ∠RSQ =∠RQP = 75° (the angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.)
In ∆RSQ,
∠RSQ + ∠SRQ + ∠RQS = 180°
⇒75° + 75° + ∠RQS = 180°
⇒ ∠RQS =30°
Solution 32
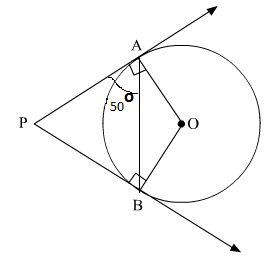

Solution 33

Solution 34
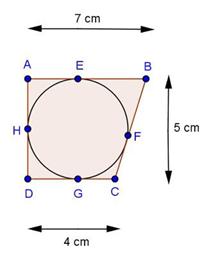

Solution 35
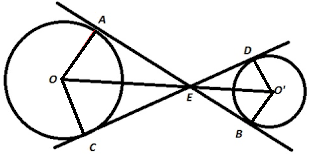

Solution 36
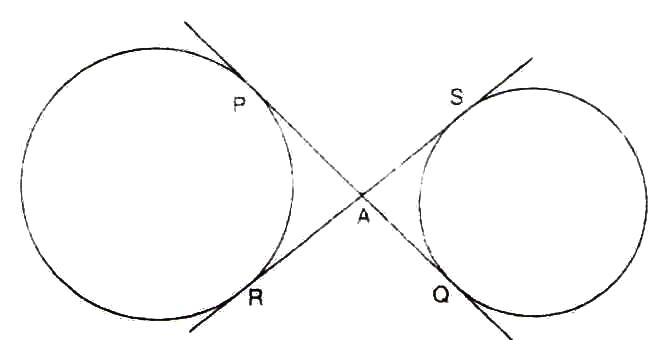

Solution 37
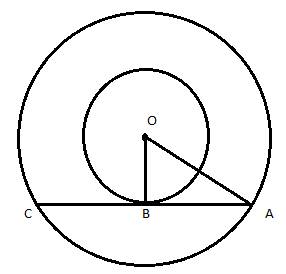
![]()
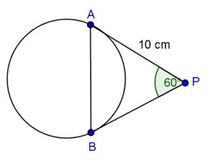
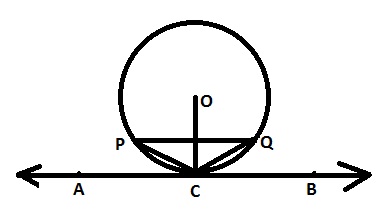
Since AC is the tangent to the circle with radius 9 cm, we have OB ⊥ AC.
Hence, by applying the Pythagoras Theorem, we have,
OA2 = OB2 + AB2
⇒ 152 = 92 + AB2
⇒ AB2 = 152 - 92
⇒ AB2 = 225 - 81 = 144
∴ AB = 12 cm
We know that the perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.
Here, OB is the perpendicular and AC is the length of the chord of the circle with radius 15 cm.
So,
AC = 2 × AB = 2 × 12 = 24 cm
Length of the chord of the larger circle which touches the smaller circle = 24 cm.
Solution 38


Solution 39
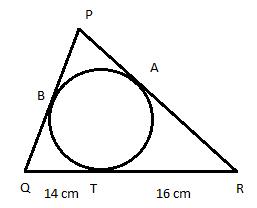
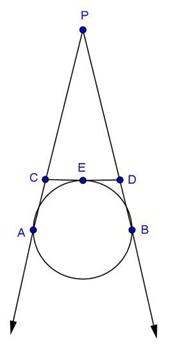
Let PA = PB = x
Tangents drawn from an external point are equal in length. QB = QT = 14 cm , RA = RT = 16 cm
PR = (x + 16) cm, PQ = (x + 14)cm,
QR = 30 cm
![]()
= x + 30
Area of ∆PQR
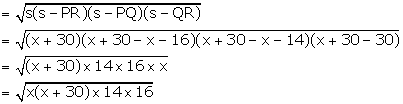
Area of ∆PQR = 336 cm2

Side PR = (12 + 16) = 28 cm
Side PQ = (12 + 14) = 26 cm
Solution 40

Solution 41
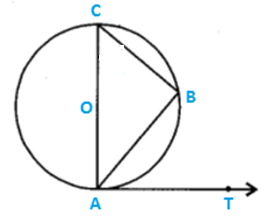
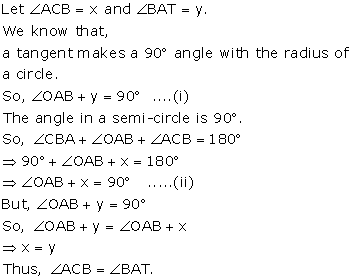
Solution 42
Let M and N be the points where AB and AC touch the circle respectively.
Tangents drawn from an external point to a circle are equal
⇒ AM=AN
BD=BM=8 cm and DC=NC=6 cm

Solution 43
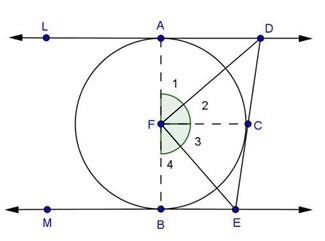
∠AOQ=58° (given)
![]()
In right ∆BAT,
∠ABT + ∠BAT + ∠ATB=180°
29° + 90° + ∠ATB=180°
∠ATB = 61°
that is, ∠ATQ = 61°
Solution 44
Solution 45
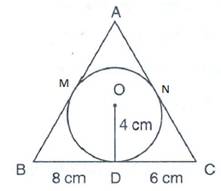
Solution 46
In ∆AOP,
OA = OP (radii) ∆AOP is an isosceles triangle. OE is a median.
In an isosceles triangle,the median drawn∴∠OEA = 90o
In ∆AOE and ∆ABC,
∠ABC = ∠OEA = 90o
∠A is common.
∆AEO ~ ∆ABC…(AA test)
Solution 47
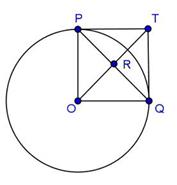

Solution 48
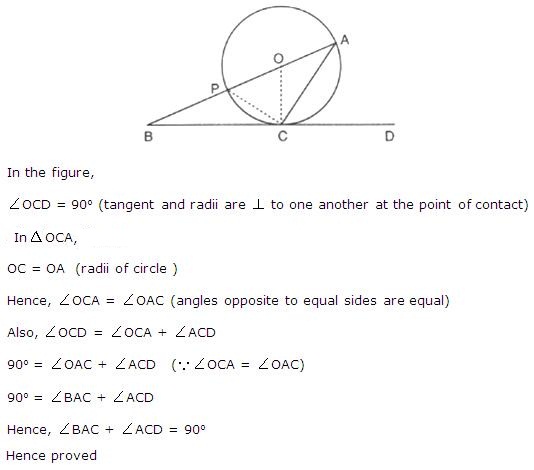
Solution 49
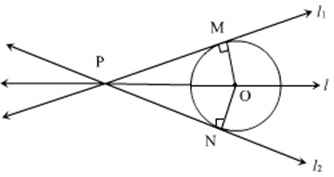

Solution 50
PR = PQ…(tangents fromexternal points)
PQ = 5 cm
Also,
OQ is perpendicular to PS …(tangent is perpendicular to the radius)
Now, in a circle,a perpendicular drawn from the centre of a circle bisects the chord.
So, OQ bisects PS.
PQ = QS
QS = 5 cm
PS = 10 cm
Solution 51
In DPQR,
∠POR is an external angle.
So,
∠POR = ∠PQO + ∠OPQ
Now, PQ is tangent to the circle with radius OQ.
∠PQO = 90o
130˚ = 90˚ + ∠OPQ
∠OPQ = 40o
∠1 = 40o
Now,
Minor arc RT subtends a 130˚ angle at the centre.
So, it will subtend a 65˚angle at any other point on the circle.∠RST = 65˚
∠2 = 65˚
∠1 + ∠2 =105˚
Solution 52
AP = PB = 12 cm, AC = CQ = 3 cm and QD = DB = 3 cm …(tangent from external point)
PA = 12 cm, PC + CA = 12
PC + 3 = 12
PC= 9 …(i)
Now,
PB = 12
PD + DB = 12
PD + 3 = 12
PD = 9 …(ii)
PC + PD = 18 cm…from (i) and (ii)
Circles Exercise 8.48
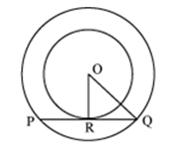
Solution 1
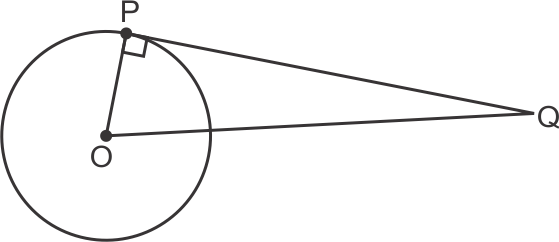
radius = 5 cm
So, OP = 5 cm
OQ = 12 cm

So, the correct option is (d).
Solution 2
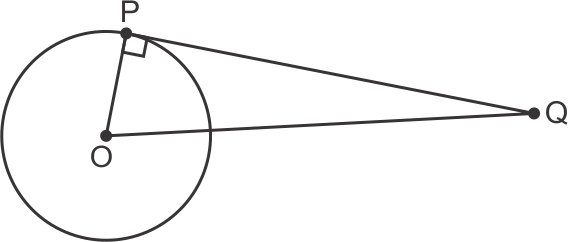
PQ is a tangent to the circle
So, OP2 + PQ2 = OQ2
OP2 = OQ2 - PQ2
= (25)2 - (24)2
= 49
OP = 7
So, the correct option is (a).
Solution 3
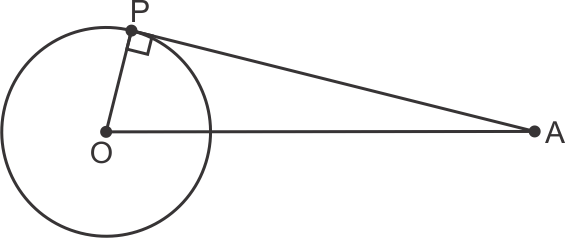
Given OP = 3 cm
PA = 4 cm
Hence, OA2 = OP2 + PA2
OA2 = 32 + 42
= 25
OA = 5 cm
So, the correct option is (c).
Solution 4

Circles Exercise 8.49
Solution 5

Solution 6
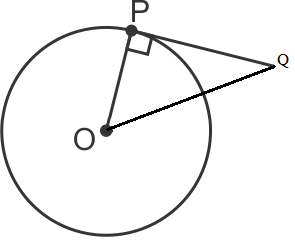

Solution 7


Solution 8
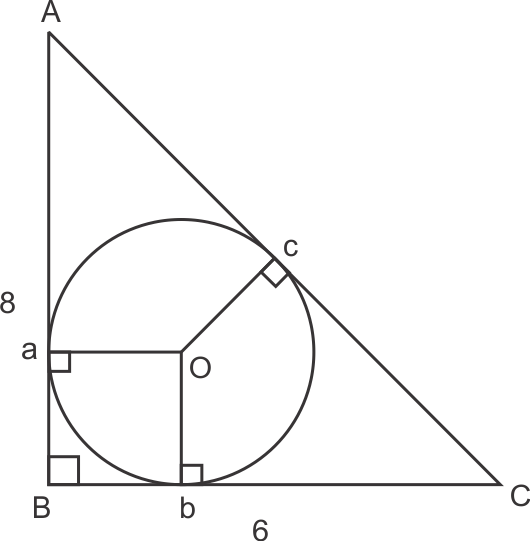
Tangents from same point to circle have equal length.
Hence Bb = Ba
bC = Cc
Ac = Aa
Let Ba = x then Bb = x
bc = 6 - x and Aa = 8 - x
and Cc = 6 - x and Ac = 8 - x
So AC = AC + cC
= 6 - x + 8 - x
AC = 14 - 2x ......(1)
Also AC2 = AB2 + BC2
= 82 + 62
= 100
AC = 10 .....(2)
from (1) & (2)
14 - 2x = 10
4 = 2x
x = 2 also aB = Ob = radius = 2 cm
So, the correct option is (b).
Solution 9
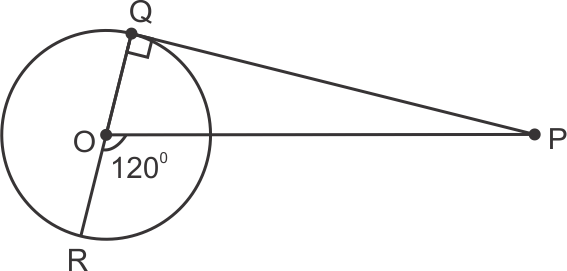

Solution 10
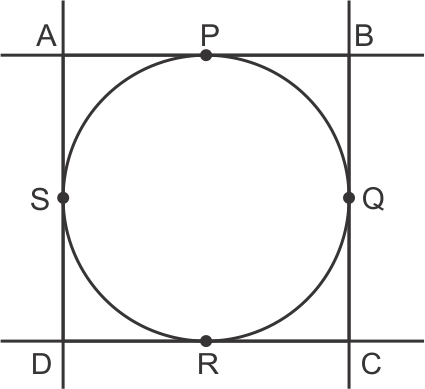
Tangents from same point are of equal length.
AP = AS, PB = BQ
QC = CR, RD = DS
AB = AP + PB .....(1)
BC = BQ + QC ......(2)
CD = CR + RD .....(3)
AD = AS + DS .....(4)
Adding (1) & (3)
AB + CD = AP + BP + CR + RD
= AS + BQ + CQ + DS
= (AS + DS) + (BQ + CQ)
from (2) & (4)
AB + CD = AD + BC
So, the correct option is (b).
Solution 11
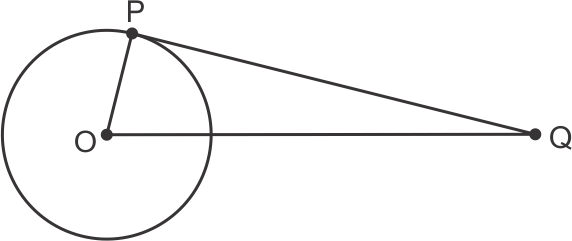
Given OQ = 8 cm
OP = 6 cm
OP2 + PQ2 = OQ2
62 + PQ2 = 82
PQ2 = 64 - 36
= 28
PQ = ![]()
So, the correct option is (b).
Solution 12
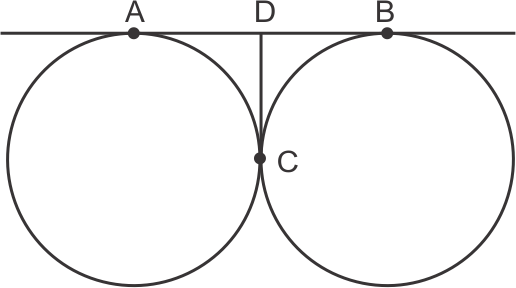
DA and DC are tangents to circle from same point
so, DA = DC ......(1)
similarly DB = DC ......(2)
(1) + (2)
2DC = DA + DB
2DC = AB
AB = 2 × 4
= 8 cm
So, the correct option is (c).
Solution 13
AD = AE .......(1)
CD = CF ......(2)
BF = BE .....(3)
from (1)
2AD = 2AE
= AE + AD
= (AB + BE) + (AC + CD)
= AB + BF + AC + CF
= AB + AC + BC
So, the correct option is (b).
Solution 14

Circles Exercise 8.50
Solution 15

Solution 16

Solution 17
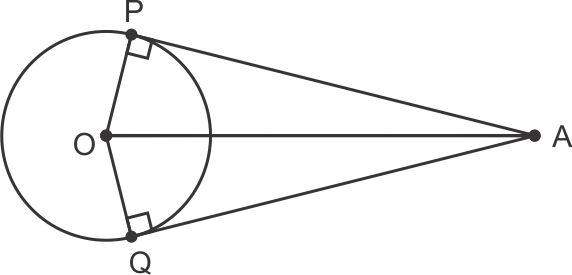
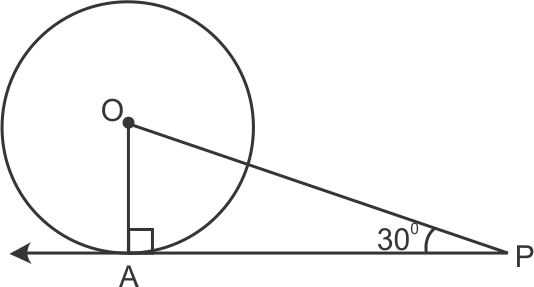
AP = PQ ....(1)
and OA2 = OP2 + PA2
(15)2 = (9)2 + AP2
AP2 = 225 - 81
= 144
AP = 12
AP + AQ = 2AP
= 24 cm
So, the correct option is (c).
Solution 18

Solution 19

Circles Exercise 8.51
Solution 20
AB = 12 cm
BC = 8 cm
AC = 10 cm
Let AD = x
AF = x
BD = 12 - x
and BE = BD = 12 - x
CE = BC - BE
= 8 - (12 - x)
= x - 4
and CE = CF = x - 4
AC = AF + FC
= x + x - 4
AC = 2x - 4
Given, AC = 10 cm
so 2x - 4 = 10
2x = 14
x = 7 cm
AD = 7 cm
So, the correct option is (d).
Solution 21
AP = BP given
and AP = AQ
also BP = BR
from this, we conclude that
AQ = BR .....(1)
We know CR = CQ .....(2)
from (1) & (2)
AQ + CR = BR + CR
AQ + CQ = BR + CR
AC = BC
So, the correct option is (b).
Solution 22
AP = 10 cm
AO = 6 cm
OB = 3 cm
AP2 + OA2 = OP2
OP2 = 102 + 62
OP2 = 136
Also OB2 + BP2 = OP2
32 + BP2 = 136
BP2 = 136 - 9
![]()
So, the correct option is (b).
Solution 23

Circles Exercise 8.52
Solution 24
PA = PD
AQ = QB
and PQ = PA + AQ
PQ = PD + QB
Hence PD + QB = PQ
So, the correct option is (a).
Solution 25
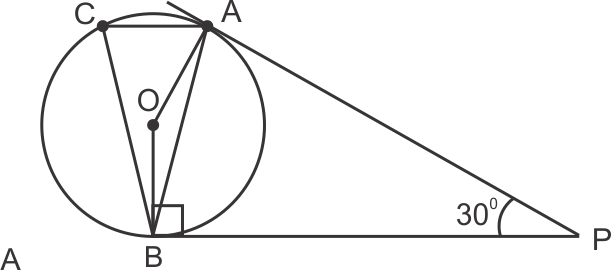
PQ = PT .....(1)
and PT = PR .....(2)
so from (1) & (2)
PQ = PR
PQ = PR = 4.5 cm
QR = PQ + PR
= 4.5 + 4.5 = 9 cm
So, the correct option is (a).
Solution 26

Solution 27

Circles Exercise 8.53
Solution 28
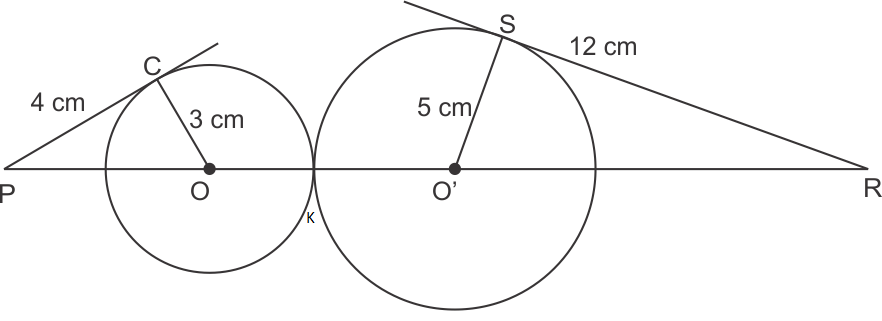
radius of circle 1 = 3 cm
radius of circle 2 = 5 cm
OP2 = OQ2 + QP2 and O'S2 + SR2 = O'R2
OP2 = 42 + 32 O'R2 = 52 + 122
= 16 + 9 O'R2 = 169
= 25 O'R' = 13 cm
OP = 5 cm
OO' = OK + KO'
= 3 + 5
= 8 cm
PR = PO + OK + KO' + O'R
= 5 + 3 + 5 + 13
= 26 cm
So, the correct option is (b).
Solution 29

Solution 30
OB = OC = OA = 5 cm
OQ = OP = 3 cm
OB2 = OQ2 + BQ2
BQ2 = OB2 - OQ2
= 52 - 32
= 16
BQ = 4 cm
also BQ = BP
BP = 4 cm
In ΔOPC,
OP2 + PC2 = OC2
PC2 = OC2 - OP2
= 52 - 32
= 16
PC = 4 cm
BC = BP + PC = 4 + 4 = 8 cm
So, the correct option is (c).
Solution 31
Given PR = 7.5 cm
so PR = PQ
PQ = 7.5 cm
PS is the chord to the larger circle. We know that, perpendicular drawn from centre bisect the chords.
Hence PQ = QS
PS = PQ + QS
= 2PQ
= 2 × 7.5
= 15 cm
So, the correct option is (c).
Circles Exercise 8.54
Solution 32
AC = AB .....(1)
BD = DP ......(2)
PE = EC ......(3)
AB = 8 so AC = 8 cm
PE = 3 so EC = 3 cm
AE = AC - EC = 8 - 3 = 5 cm
So, the correct option is (c).
Solution 33

Solution 34

Circles Exercise 8.55
Solution 35
PA = AR
AR = 4 cm
BP = BQ and QC = RC
BQ = 3 cm
Given AC = 11
AR + RC = 11
4 + RC = 11
RC = 7
so QC = 7 cm
BC = BQ + QC
= 3 + 7
= 10 cm
So, the correct option is (b).
Solution 36
EK = 9 cm
and EK = EM
Hence EM = 9 cm .....(1)
Also EK = ED + DK
and DK = DH
EK = ED + HD .......(2)
EM = EF + FM
and FM = FH
EM = EF + FH ......(3)
(2) + (3)
EK + EM = ED + EF + DH + HF
18 = ED + DF + EF
perimeter = 18 cm
So, the correct option is (a).
Solution 37

Circles Exercise 8.56
Solution 38

AB = 29 cm
AD = 23
DS = 5 cm
DS = DR
so DR = 5 cm
AR = AD - DR
= 23 - 5
= 18 cm
AR = AQ
AQ = 18 cm
BQ = AB - AQ
= 29 - 18
BQ = 11 cm
As OP || BQ and OQ || PB
Hence, OP = BQ
OP = 11 cm
So, the correct option is (a).
Solution 39
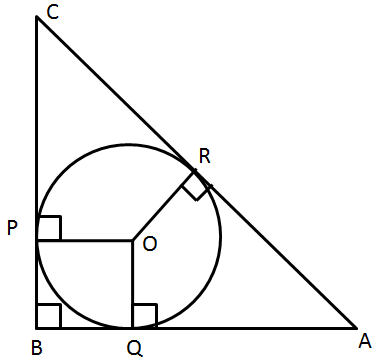
AB = 5 cm
BC = 12 cm
AB2 + BC2 = AC2
AC2 = 52 + 122
= 169
AC = 13 cm
Let BQ = x
AQ = AR = 5 - x
CR = AC - AR
= 13 - (5 - x)
= x + 8
And CP = CR = x + 8
so BP = BC - PC
= 12 - (x + 8)
= 4 - x
But BP = BQ = x
4 - x = x
x = 2
and BQ || OP and OQ || PB
so BQ = PO
PO = 2 cm
So, the correct option is (c).
Solution 40

Solution 41

Solution 42
PT = 3.8 cm
We know
PQ = PT and PT = PR
Hence PQ = 3.8 cm and PR = 3.8 cm
Now, QR = QP + PR
= 3.8 + 3.8
QR = 7.6 cm
So, the correct option is (b).
Circles Exercise 8.57
Solution 43
AB = x cm
BC = 7 cm
CR = 3 cm
AS = 5 cm
CR = CQ
CQ = 3 cm
given BC = 7 cm
BQ = BC - QC
= 7 - 3
= 4 cm
And BQ = BP
so BP = 4 cm
Also AS = AP
Hence AP = 5 cm
AB = AP + BP
= 5 + 4
= 9 cm
x = 9 cm
So, the correct option is (b).
Solution 44


Solution 45


Solution 46

Solution 47
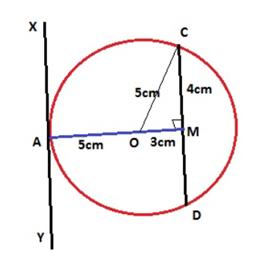

Solution 48


Solution 49


Solution 50


Circles Exercise 8.58
Solution 51

Solution 52