Class 10 SELINA Solutions Maths Chapter 17 - Circles
TopperLearning helps you with chapter-wise Selina solutions according to the latest guidelines of the ICSE board. Here, you have the accurate step-by-step solutions available 24 x 7, letting you indulge in a seamless journey of self-paced learning. All the Class 10 Selina solutions for Maths chapter 17 - Circles are explained chronologically, with adequate diagrams offering proper understanding.
The Class 10 Selina Solutions for Maths are specifically crafted by professional subject matter experts at TopperLearning who are well-versed with the latest ICSE Class 10 Math syllabus and have followed all the guidelines keeping the ICSE exam pattern and marking strategy in mind.
Browse the Class 10 Selina solutions for Maths chapter 17 - Circles page and work on individual concepts. Moreover, you will come across no answer that leaves you wondering why. You will find reasonable explanations doing appropriate justice to each step and every answer.
When preparing for your board exams, you must be extra careful and have a fixed schedule planned to score the maximum grades. And with the entire syllabus, question papers and the right solutions, things get easy.
At TopperLearning, you will also get all the ICSE Class 10 syllabus, previous year's question papers with solutions, video lessons, revision notes, sample papers and solutions in Maths.
For students looking for accurate Selina solutions in Class 10 Biology, Physics, and Chemistry other than Mathematics, TopperLearning has the best resources readily available. As an additional help, here you will find the right outputs for doubts in English, Hindi, Social Studies and Economics.
Circles Exercise Ex. 17(A)
Solution 1
Solution 2
Solution 3
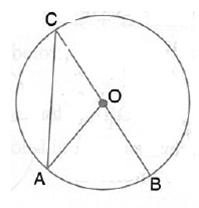
Solution 4
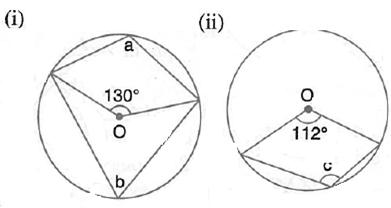
Solution 5
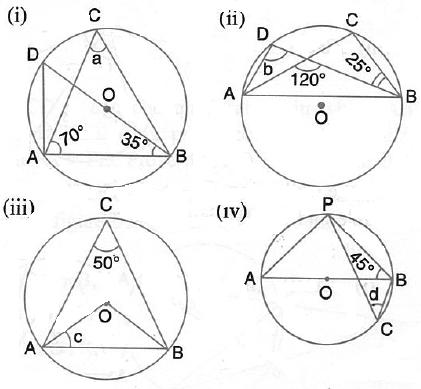
Solution 6
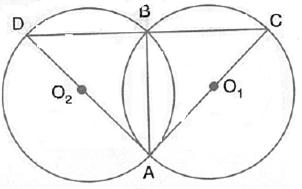
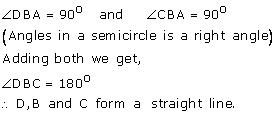
Solution 7
Solution 8
Solution 9
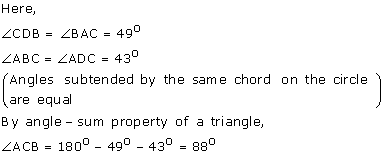
Solution 10
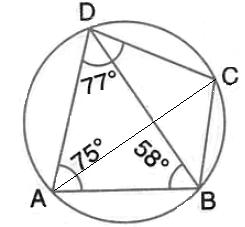
Solution 11
Solution 12
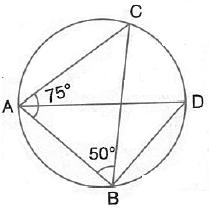
Solution 13
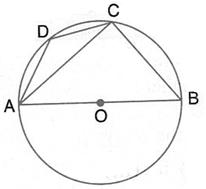
Solution 14
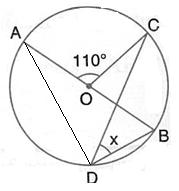
Solution 15
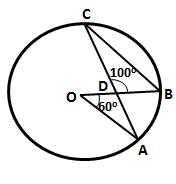
Solution 16
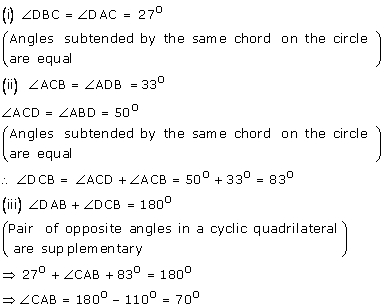
Solution 17
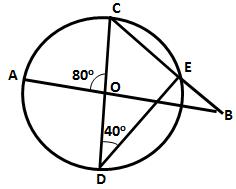
Solution 18
Solution 19
Solution 19(b)
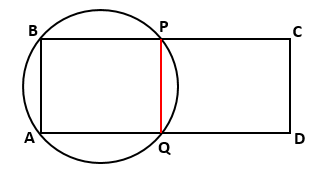
▭ABPQ is a cyclic quadrilateral.
⟹∠A = ∠P …..(Exterior angle property of cyclic quadrilateral) …(1)
▭ABCD is a parallelogram.
⟹ ∠A = ∠C …..(Opposite angles of a parallelogram) ….. (2)
From (1) and (2),
∠P = ∠C…..….(3)
But ∠C + ∠D = 180° …. (Sum of interior angles of a parallelogram is 180°)
From (3), we get
∠P + ∠D = 180°
⟹ PCDQ is a cyclic quadrilateral.
Solution 20
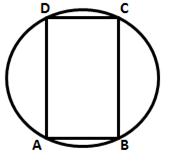
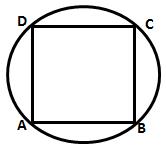
Solution 21
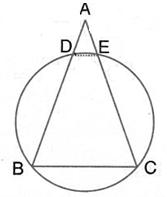
Solution 22
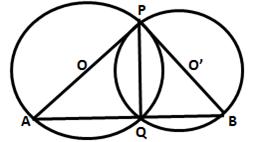
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
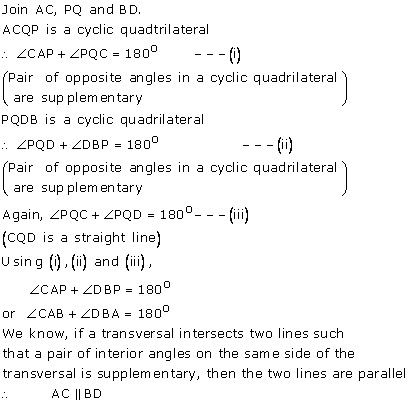
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32
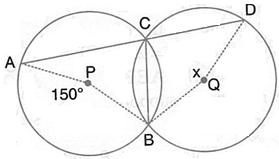
Solution 33
Solution 34
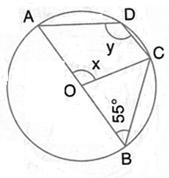
Solution 35
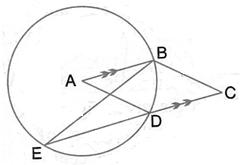
Solution 36
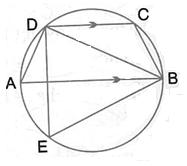
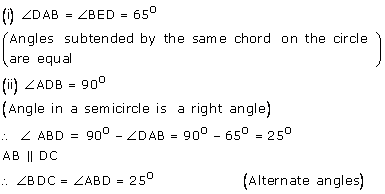
Solution 37
(i) 
AEB = 
(Angle in a semicircle is a right angle)
Therefore EBA = - EAB = - 
= 
(ii) AB 
ED
Therefore DEB = EBA = (Alternate angles)
Therefore BCDE is a cyclic quadrilateral
Therefore DEB + BCD = 
[Pair of opposite angles in a cyclic quadrilateral are supplementary]
Therefore BCD = - = 
Solution 38
Solution 39
Solution 40
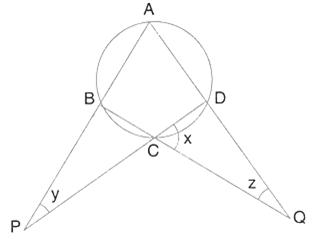
Solution 41
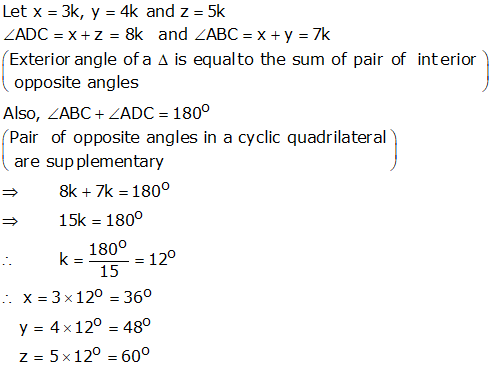
Solution 42
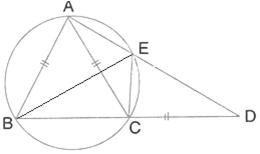
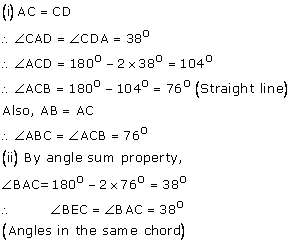
Solution 43
Solution 44
Solution 45
Solution 46
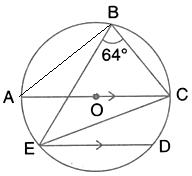
Solution 47
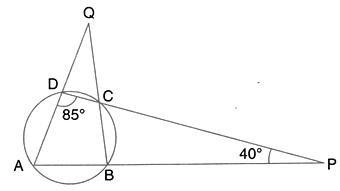
Solution 48
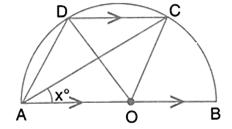
Solution 49
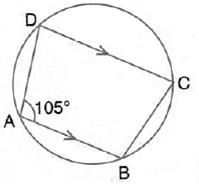
- ABCD is a cyclic quadrilateral
m∠DAB = 180° - ∠DCB
= 180° - 130°
= 50°
- In ∆ADB,
m∠DAB + m∠ADB + m∠DBA = 180°
⇒50° + 90° + m∠DBA = 180°
⇒m∠DBA = 40°
Solution 50
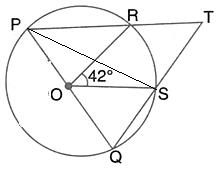
Solution 51
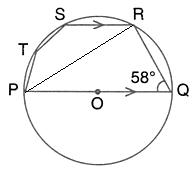
Solution 52
Solution 53
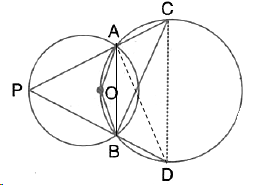
Solution 54
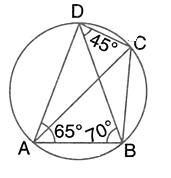
Solution 55
Solution 56
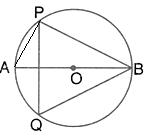
Solution 57
Circles Exercise Ex. 17(B)
Solution 1
Solution 2
Solution 3
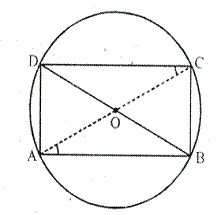
Solution 4
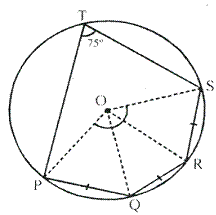
Solution 5
Solution 6
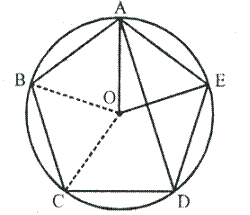
Solution 7
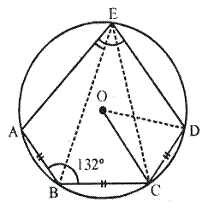
Solution 8
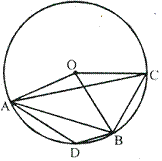
Solution 9
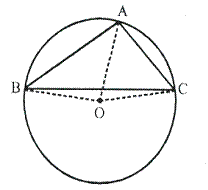
Solution 10
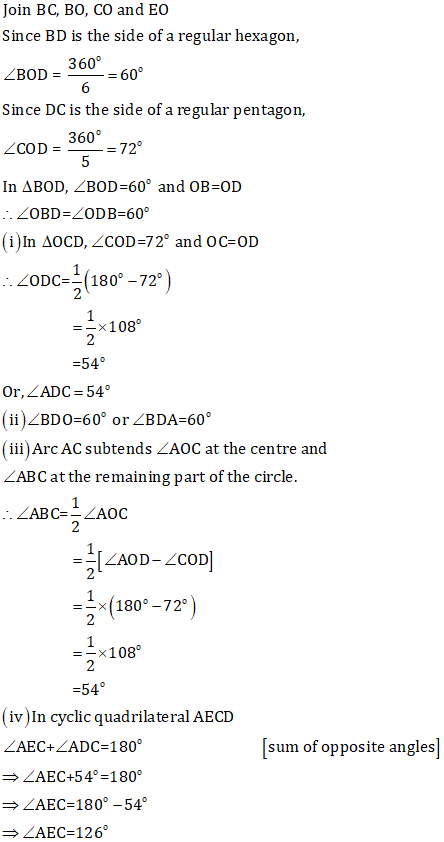
Circles Exercise Ex. 17(C)
Solution 1
Solution 2
Solution 3
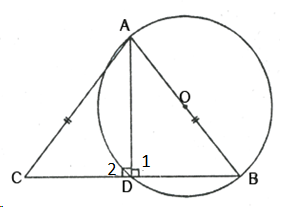
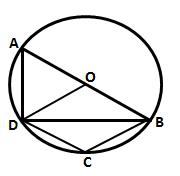
Given - In Δ ABC, AB = AC and a circle with AB as diameter is drawn which intersects the side BC at D.
To prove - D is the midpoint of BC.
Construction - Join AD.
Proof:
∠1 = 90° [Angle in a semi circle]
But ∠1 + ∠2 = 180° [Linear pair]
∴ ∠2 = 90°
Now in right ΔABD and Δ ACD,
Hyp. AB = Hyp. AC [Given]
Side AD = Ad [Common]
∴ By the Right angle - Hypotenuse - Side criterion of congruence, we have
Δ ABD ≅ ΔACD [RHS criterion of congruence]
The corresponding parts of the congruent triangles are congruent.
∴ BD = DC [c.p.c.t]
Hence D is the mid point of BC.
Solution 4
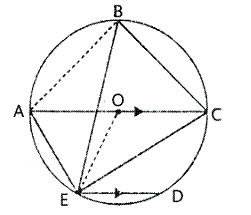
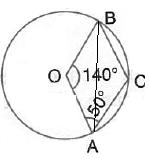
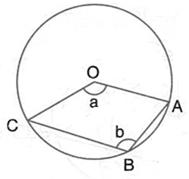
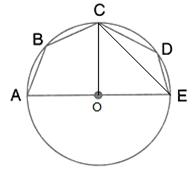
Join OE.
Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∠EOC = 2 ∠EBC = 2 × 65° = 130°.
Now in Δ OEC, OE = OC [Radii of the same circle]
∴ ∠OEC = ∠OCE
But, in Δ EOC,
∠OEC + ∠OCE + ∠EOC = 180° [Angles of a triangle]
⇒ ∠OCE + ∠OCE + ∠EOC = 180°
⇒ 2 ∠OCE + 130° = 180°
⇒ 2 ∠OCE = 180° - 130°
⇒ 2 ∠OCE + 50°
⇒ ∠OCE = 
= 25°
∴ AC || ED [given]
∴ ∠DEC = ∠OCE [Alternate angles]
⇒ ∠DEC = 25°
Solution 5
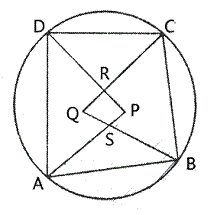
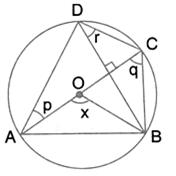
Given - ABCD is a cyclic quadrilateral and PRQS is a quadrilateral formed by the angle.
Bisectors of angle ∠A, ∠B, ∠C and ∠D.
To prove - PRQS is a cyclic quadrilateral.
Proof - In Δ APD,
∠PAD + ∠ADP + ∠APD = 180° ......(1)
Similarly, in Δ BQC,
∠QBC + ∠BCQ + ∠BQC = 180° ......(2)
Adding (1) and (2), we get
∠PAD + ∠ADP + ∠APD + ∠QBC + ∠BCQ + ∠BQC = 180° + 180°
⇒ ∠PAD + ∠ADP + ∠QBC + ∠BCQ + APD + ∠BQC = 360° ....(3)
But ∠PAD + ∠ADP + ∠QBC + ∠BCQ = 1/2 [∠A + ∠B + ∠C + ∠D]
= 1/2 × 360° = 180°
∴ ∠APD + ∠BQC = 360° - 180° = 180° [from (3)]
But these are the sum of opposite angles of quadrilateral PRQS.
∴ Quad. PRQS is a cyclic quadrilateral.
Solution 6
Solution 7
Solution 8
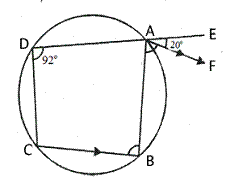
Solution 9
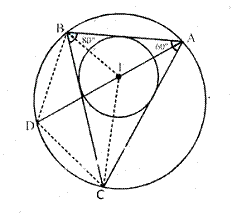
Solution 10
Solution 11
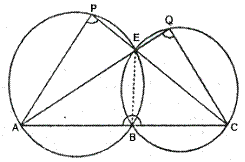
Solution 12
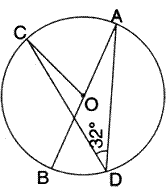
Solution 13
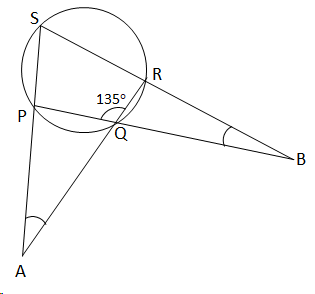
Solution 14
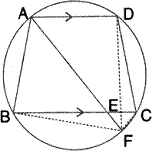
Solution 15
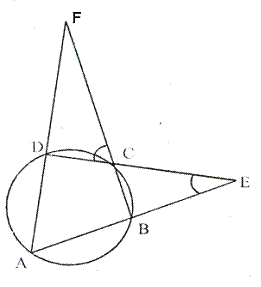
Solution 16
Solution 17
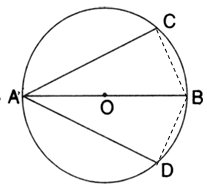
Solution 18
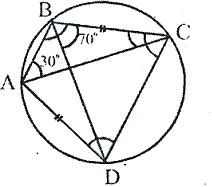
Solution 19
Solution 20
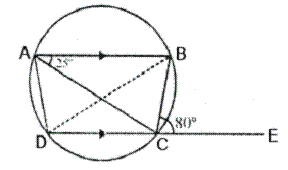
Solution 21
Solution 22
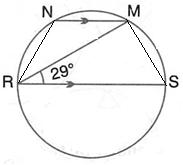
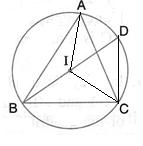
Given - In the figure, CP is the bisector of ∠ABC
To prove - DP is the bisector of ∠ADB
Proof - Since CP is the bisector of ∠ACB
∴ ∠ACP = ∠BCP
But ∠ACP = ∠ADP [Angles in the same segment of the circle]
and ∠BCP = ∠BDP
But ∠ACP = ∠BCP
∴ ∠ADP = ∠BDP
∴ DP is the bisector of ∠ADB
Solution 23
Solution 24
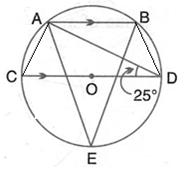
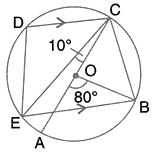
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal.
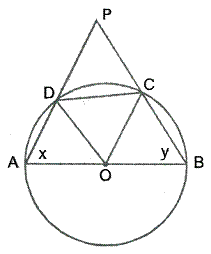
Solution 25
∠DAE and ∠DAB are linear pair
So,
∠DAE + ∠DAB = 180°
∴∠DAB = 110°
Also,
∠BCD + ∠DAB = 180°……Opp. Angles of cyclic quadrilateral BADC
∴∠BCD = 70°
∠BCD = 
∠BOD…angles
subtended by an arc on the center and on the circle
∴∠BOD = 140°
In ΔBOD,
OB = OD……radii of same circle
So,
∠OBD =∠ODB……isosceles triangle theorem
∠OBD + ∠ODB + ∠BOD = 180°……sum of angles of triangle
2∠OBD = 40°
∠OBD = 20°
