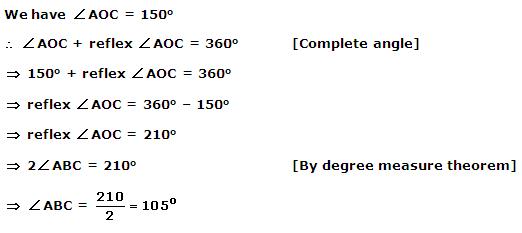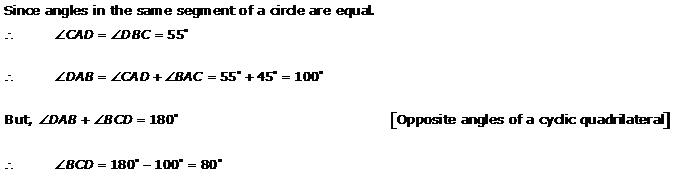Class 9 RD SHARMA Solutions Maths Chapter 15 - Circles
With TopperLearning’s chapter-wise, R.D Sharma solutions, you have the best-ever resources to learn from. While Class 9 students usually regard Maths as challenging, things become easy with the right examples at your convenience. These class 9 solutions for chapter 15 - Circles have step-by-step answers for all the exercises from the main book rightfully explained.
While devising the solutions about circles, experienced subject matter experts did follow the latest CBSE class 9 Maths guidelines. Every answer is set chronologically according to the exercise question numbers. Moreover, its detailed elaborations help you comprehensively understand various theorems and problems related to circles. Overall, aiming to make learning easy and fun for students.
Also, at TopperLearning, students can score the highest grades with interactive video lessons about circles and amplify their preparation schedule with rightfully conducted mock tests. For classes 1 to 12, you have all the necessary resources rightfully available. Besides offering exclusive R.D Sharma solutions for class 9, the website also lets you avail of R.D Sharma Solutions for class 10, R.D Sharma solutions for class 11, and R.D Sharma solutions for class 12.
The motive is to make online education affordable and seamless for all, and TopperLearning, with its exclusive set of curated modules, has the best experience to offer. When done with class 9 Maths, you can browse through the platform to access essential study materials on all other subjects like - Social Studies, Hindi, English and Maths.
Also, there are readily available creative foundations courses for the students of classes 9 and 10, helping them prepare for entrance exams like NEET and JEE. Because everything is online, you can choose and learn per your schedule and score the best grades.
Circles Exercise Ex. 15.1
Solution 1
(i) interior/exterior
(ii) concentric
(iii) the exterior
(iv) arc
(v) diameter
(vi) semi-circle
(vii) centre
(viii) three
Solution 2
(i) T
(ii) T
(iii) T
(iv) F
(v) T
(vi) T
(vii) F
(viii) T
Circles Exercise Ex. 15.2
Solution 1
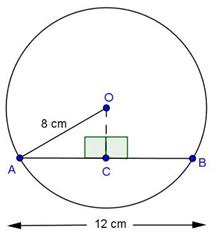
Solution 2
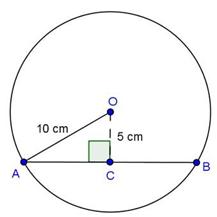
Solution 3
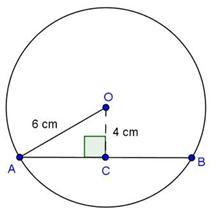
Solution 4
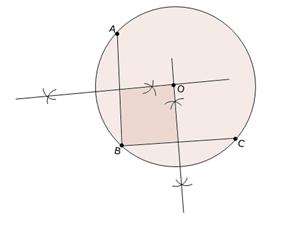
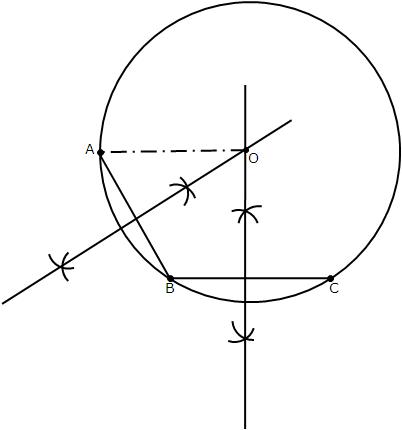
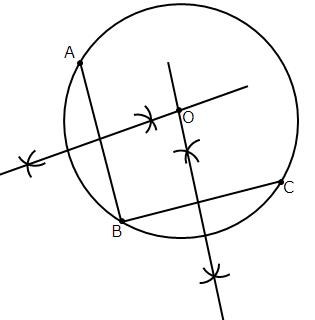
Steps of construction:
(1) Take three point A, B and C on the given circle.
(2) Join AB and BC.
(3) Draw the perpendicular bisectors of chord AB and BC which interesect each other at O.
(4) Point O will be the required circle because we know that the perpendicular bisector of a chord always passes through the centre.
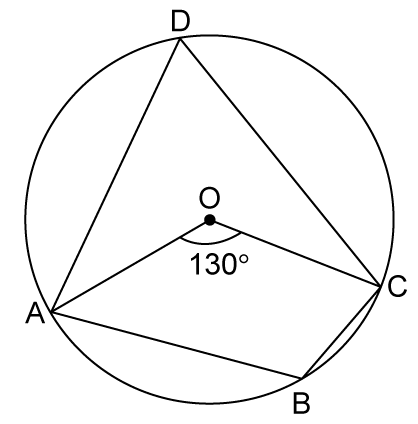
Solution 5
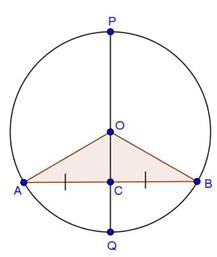
Solution 6
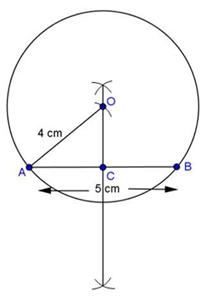
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
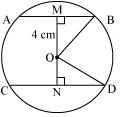
OM = 4 cm
OMB
OND
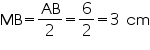
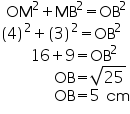
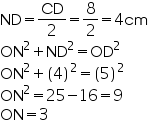
Solution 12
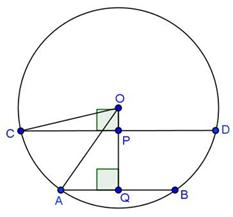
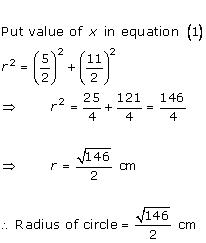
Solution 13
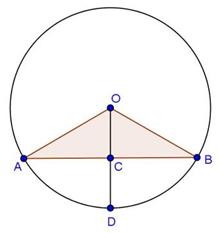
Solution 14
Suppose two different circles can intersect each other at three points then they will pass through the three common points but we know that there is one and only one circle with passes through three non-collinear points, which contradicts our supposition.
Hence, two different circles cannot intersect each other at more than two points.
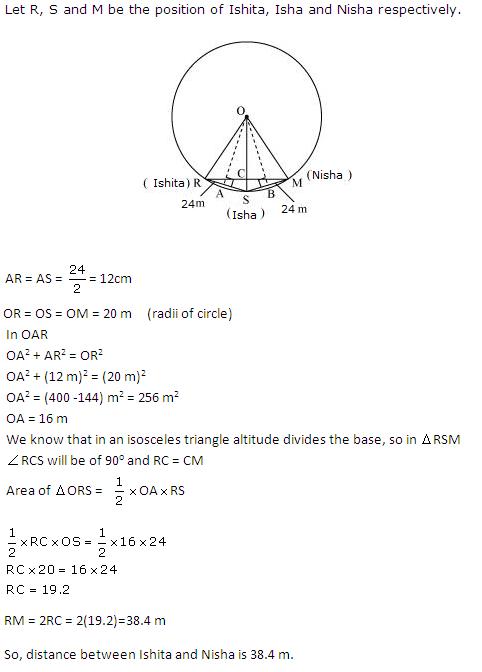
Solution 15
AB and ON CD. Join OB and OD
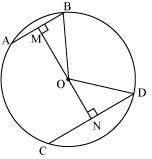
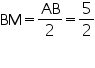(Perpendicular from centre bisects the chord)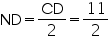
In
MOB
NOD
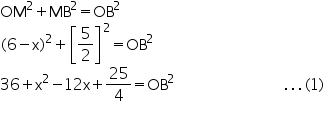
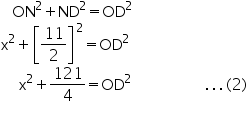
So, from equation (1) and (2)
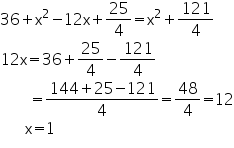
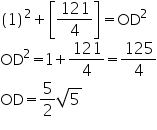
cm.Circles Exercise Ex. 15.3
Solution 1
Solution 2
Circles Exercise Ex. 15.4
Solution 1
Solution 2
Solution 3(i)
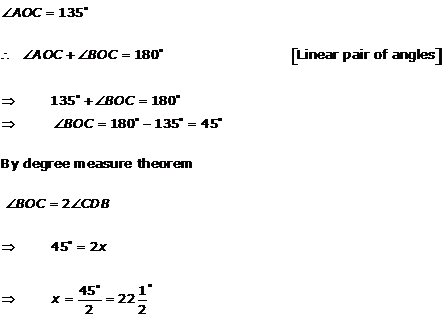
Solution 3(ii)
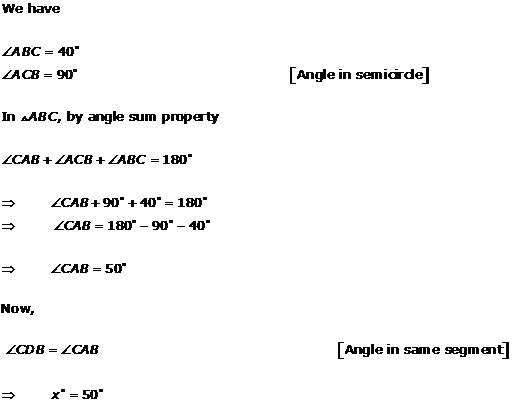
Solution 3(iii)
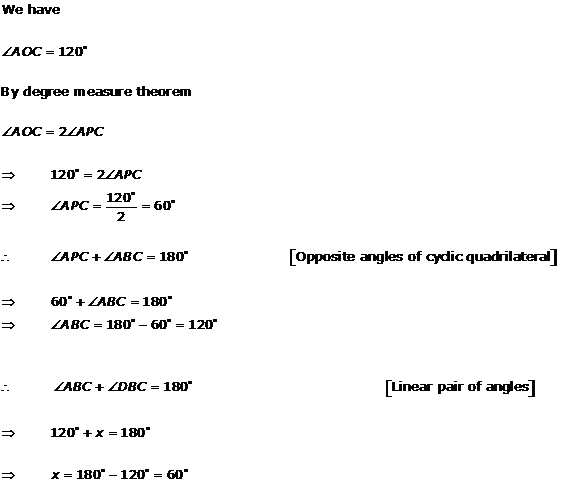
Solution 3(iv)
Solution 3(v)
Solution 3(vi)
Solution 3(vii)
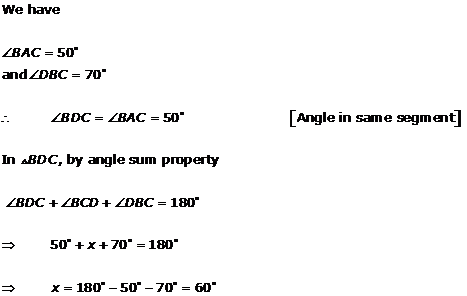
Solution 3(viii)
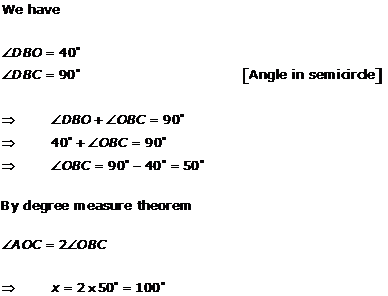
Solution 3(ix)
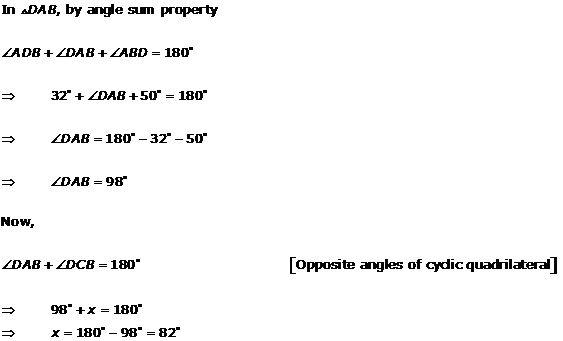
Solution 3(x)
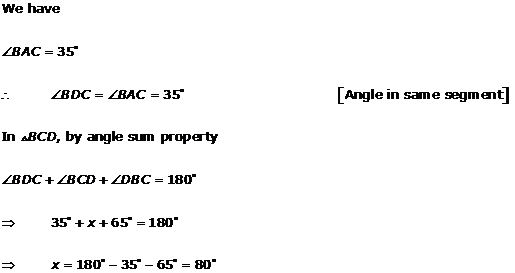
Solution 3(xi)
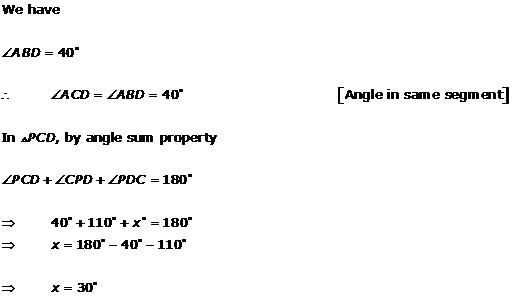
Solution 3(xii)
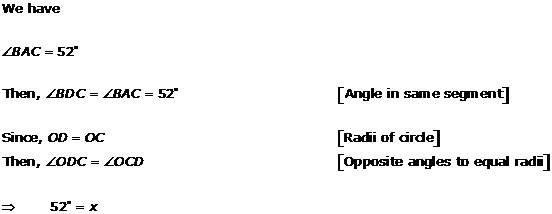
Solution 4
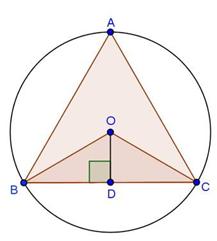
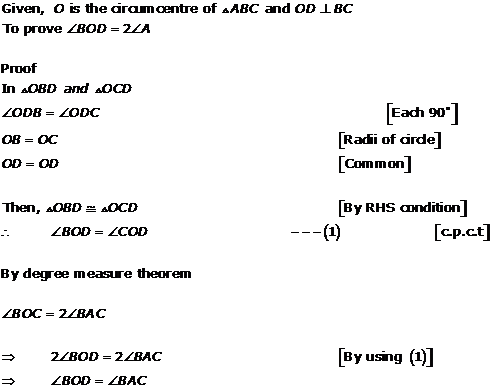
Solution 5
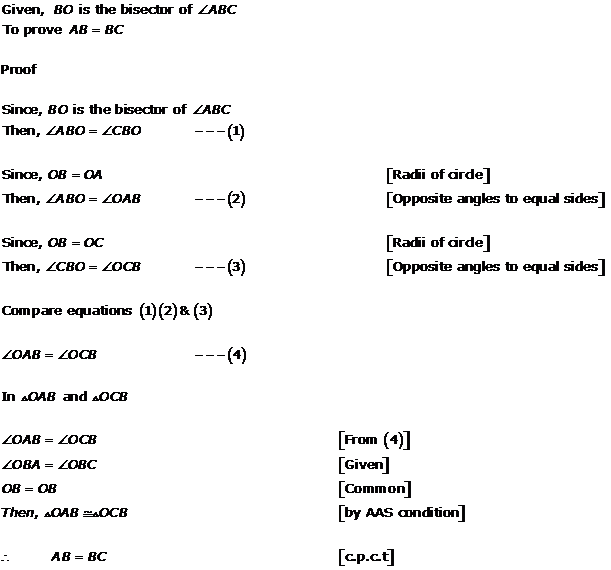
Solution 6
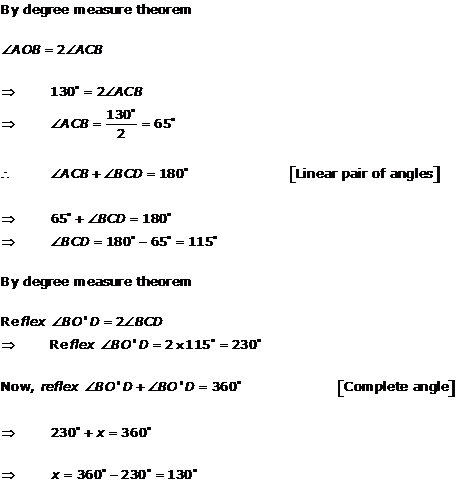
Solution 7
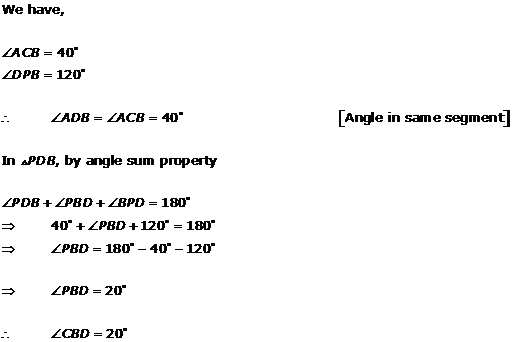
Solution 8
Solution 9
Solution 10
Solution 11
Circles Exercise Ex. 15.5
Solution 1
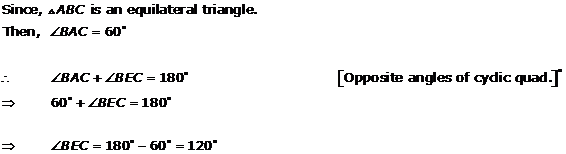
Solution 2
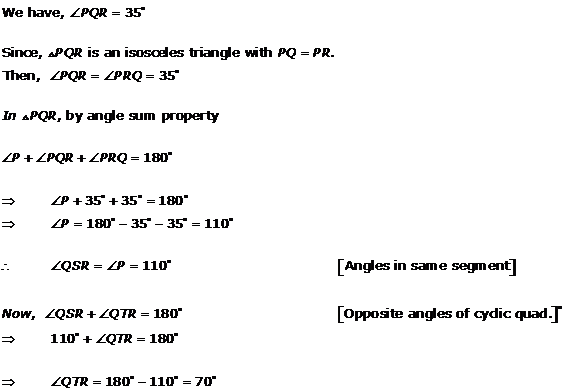
Solution 3
Solution 4
Solution 5
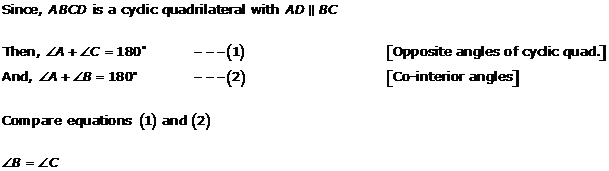
Solution 6
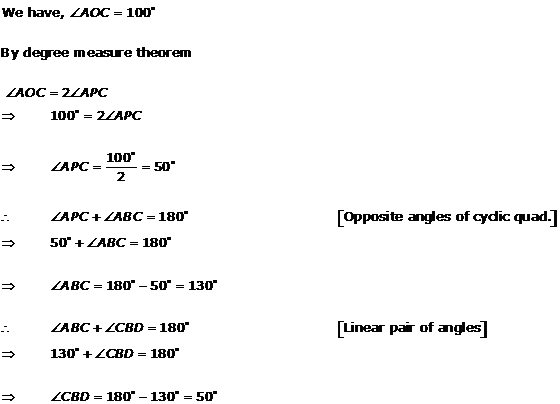
Solution 7
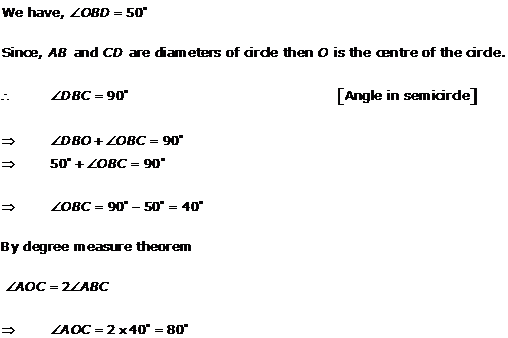
Solution 8
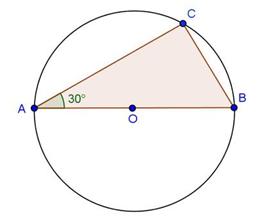
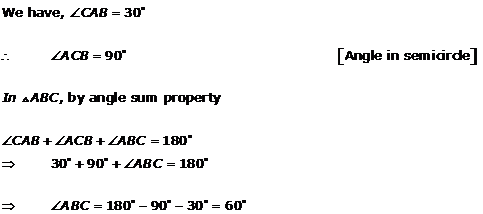
Solution 9
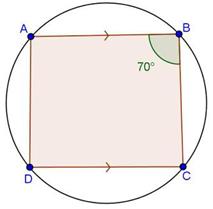
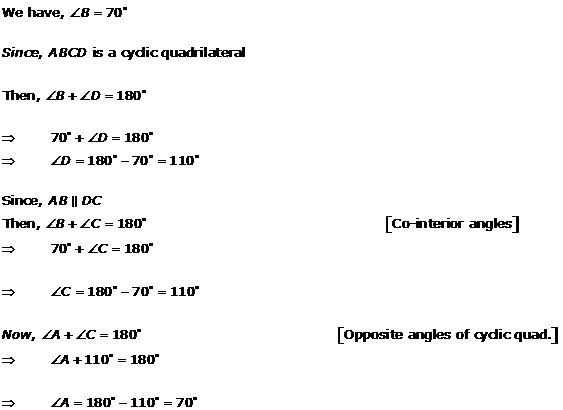
Solution 10
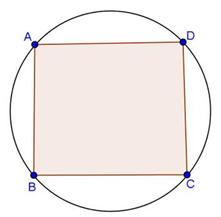
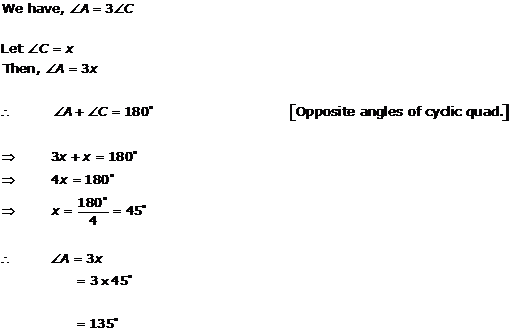
Solution 11
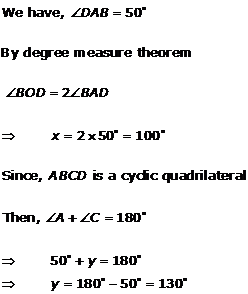
Solution 12
Solution 13
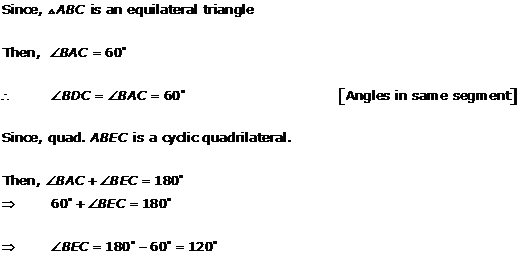
Solution 14
Solution 15
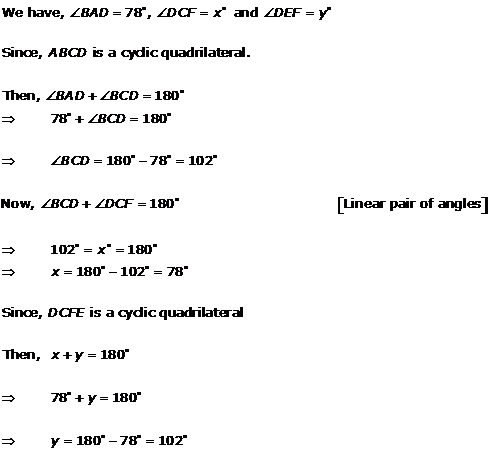
Solution 16
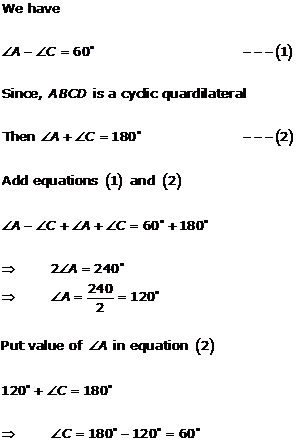
Solution 17
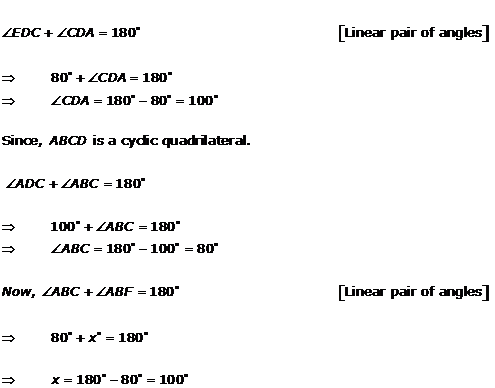
Solution 18(i)
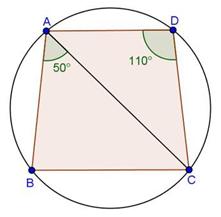
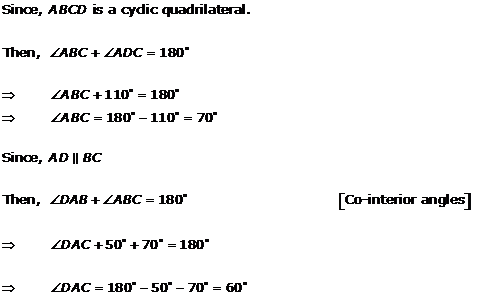
Solution 18(ii)
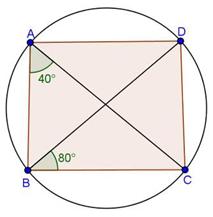
Solution 18(iii)
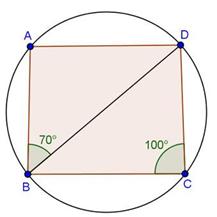
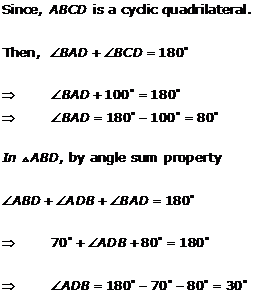
Solution 19
Solution 20
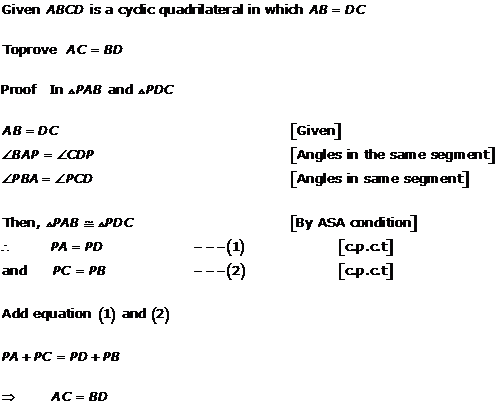
Solution 21
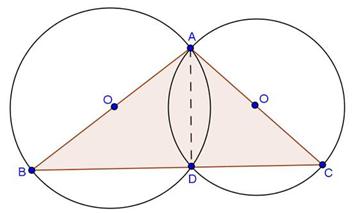
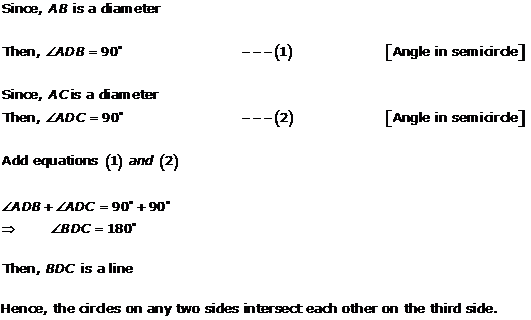
Solution 22
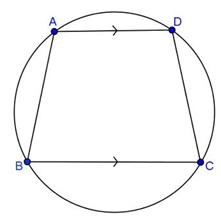
Solution 23
Solution 24
Solution 25
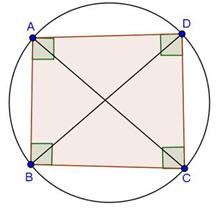
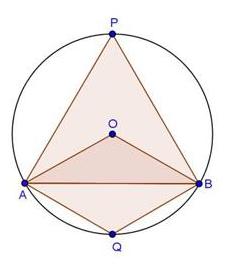
Let O be the centre of the circle circumscribing the cyclic rectangle ABCD. Since 
ABC = 90o and AC is a chord of the circle, so, AC is a diameter of the circle. Similarly, BD is a diameter.
Hence, point of intersection of AC and BD is the centre of the circle.
Solution 26
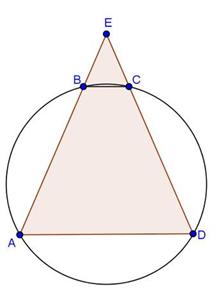
Solution 27
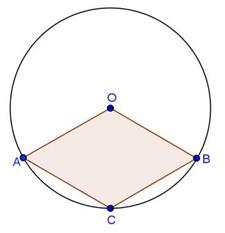
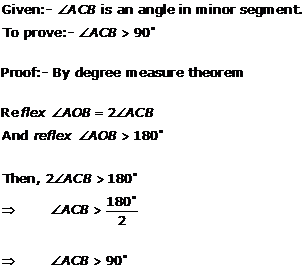
Solution 28
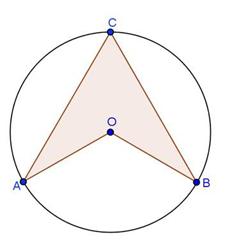
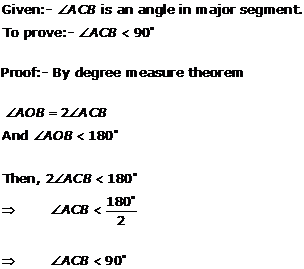
Solution 29
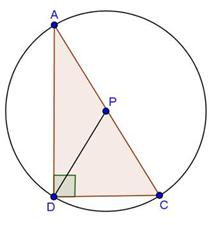
Circles Exercise 15.109
Solution 1
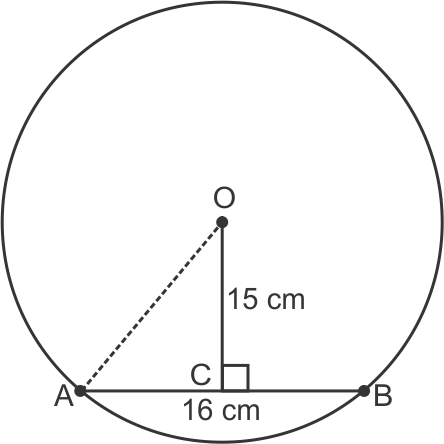
Solution 2
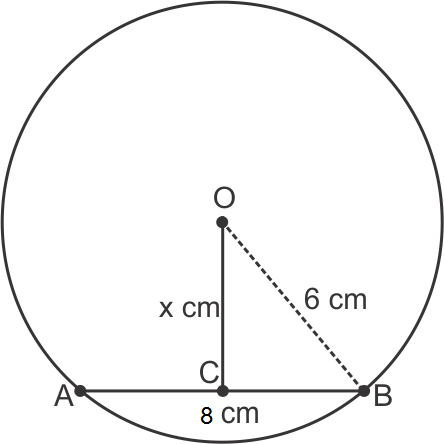
Circles Exercise 15.110
Solution 3
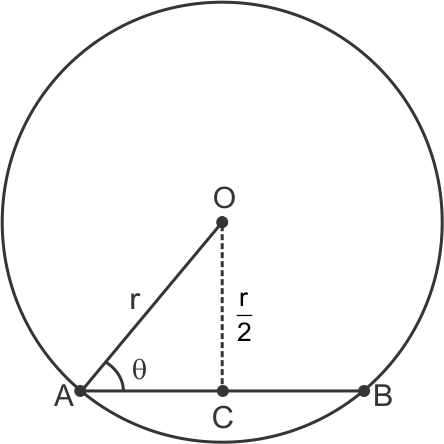
Solution 4
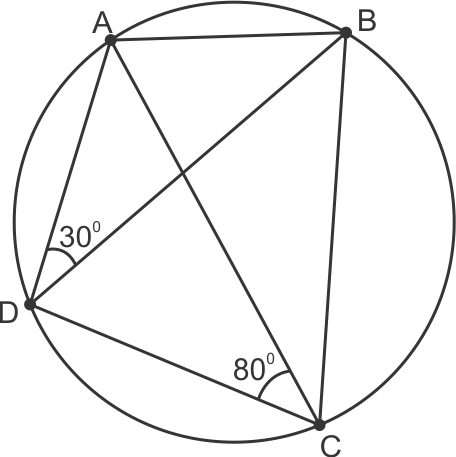
Solution 5
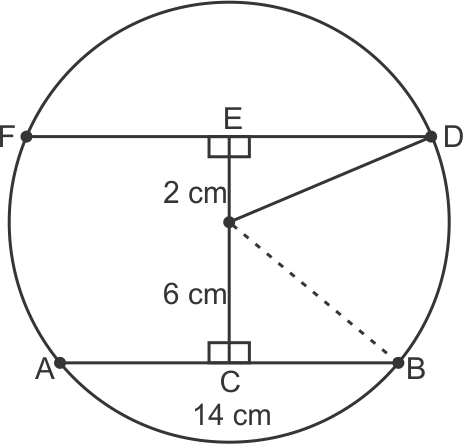
Solution 6
Solution 7
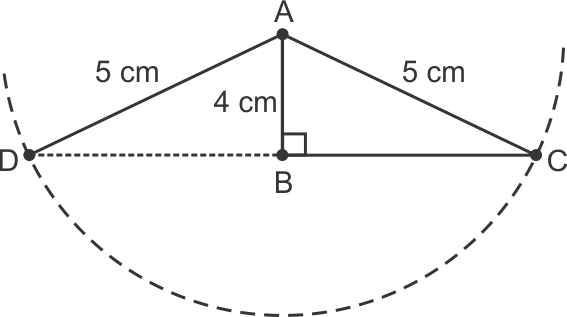
Solution 8
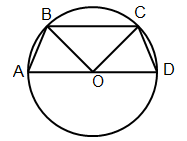
Solution 9
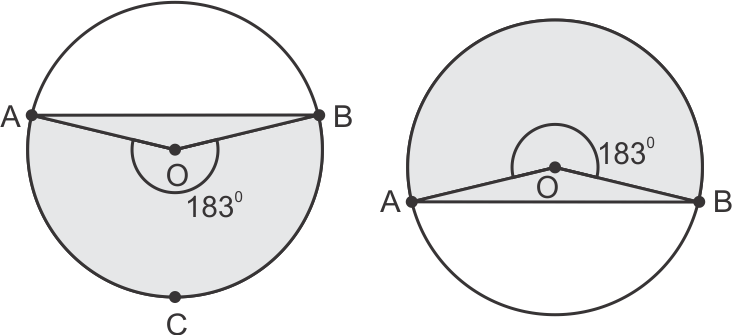
Solution 10
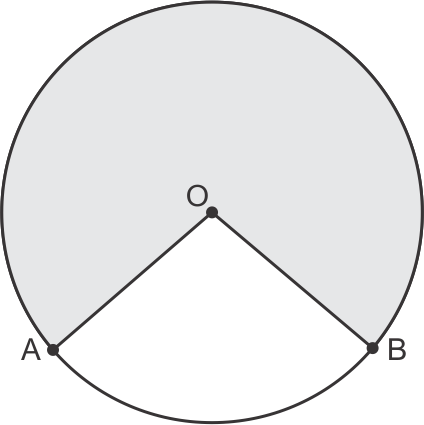
Solution 11
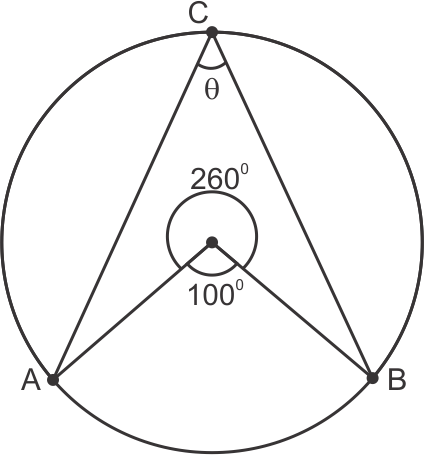
Solution 12
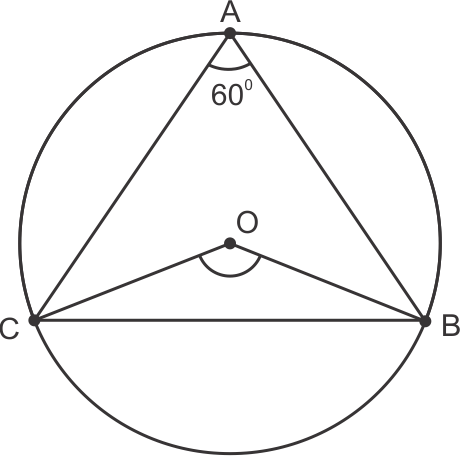
Solution 13
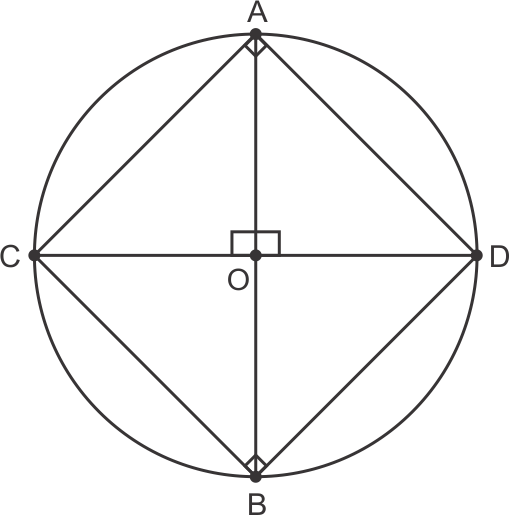
Solution 14
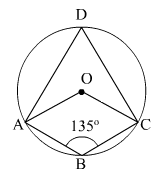
Solution 15
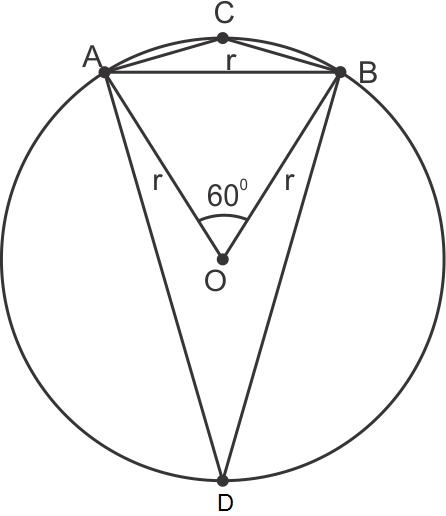
Circles Exercise 15.111
Solution 16
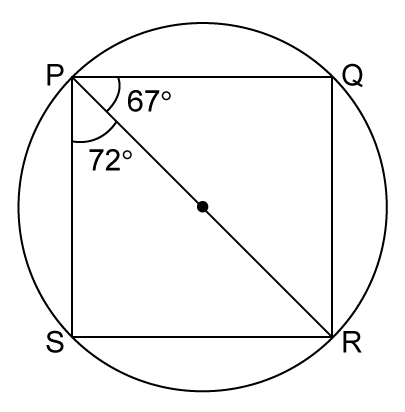
Solution 17
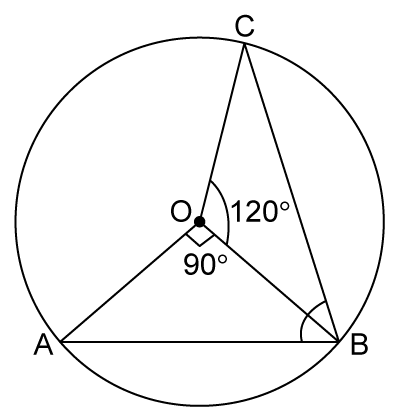
Solution 18
The greatest chord of the circle is diameter of the circle.
Hence, correct option is (c).
Solution 19
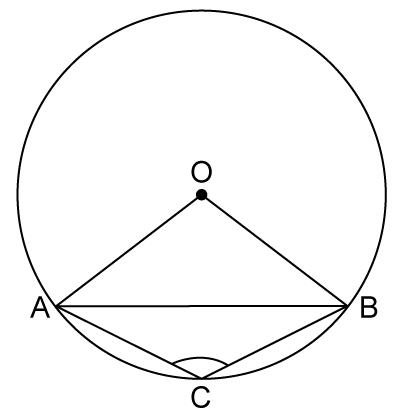
Angle formed in a minor segment is always a obtuse angle.
Hence, correct option is (b).
Solution 20
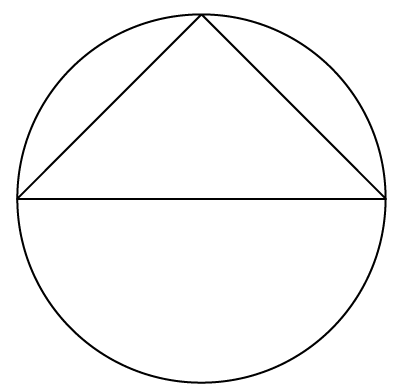
Three non-collinear points make a triangle and there is only one circle that can pass through all three points,
i.e. circumcircle of that triangle.
Hence, correct option is (a).
Solution 21
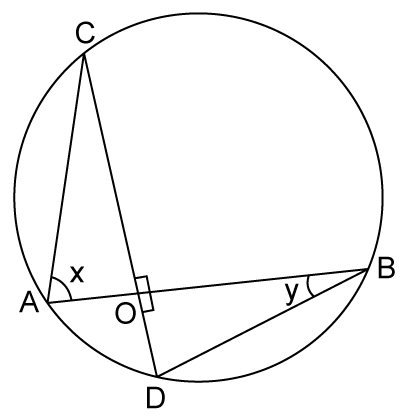
Solution 22
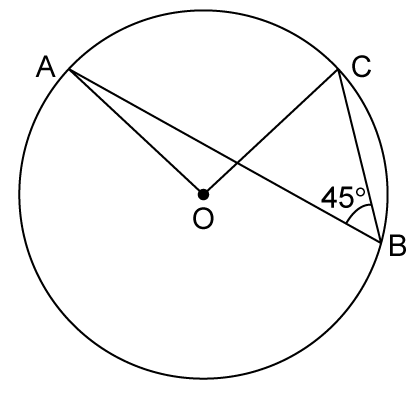
Solution 23
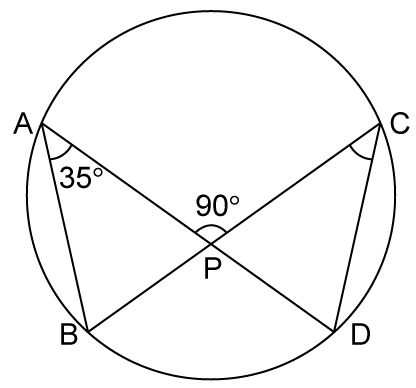
Solution 24
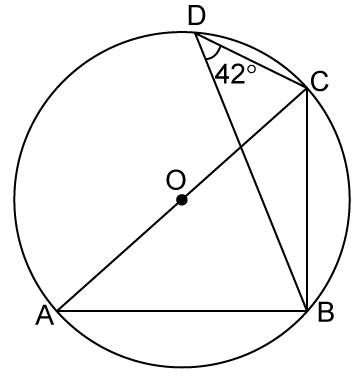
Circles Exercise 15.112
Solution 25
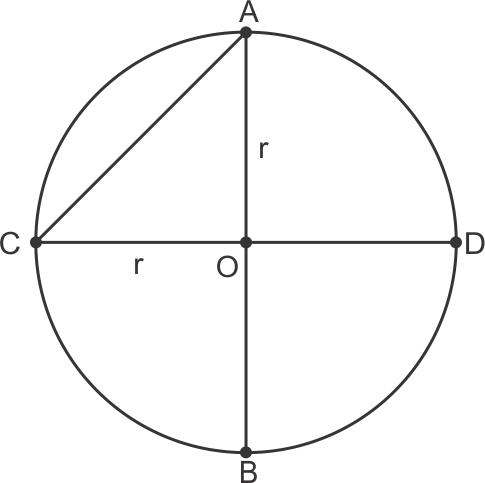
Solution 26
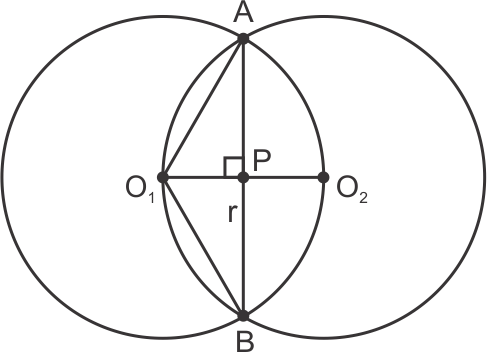
Solution 27
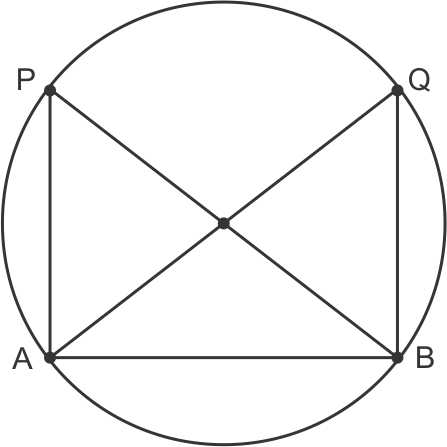
Solution 28
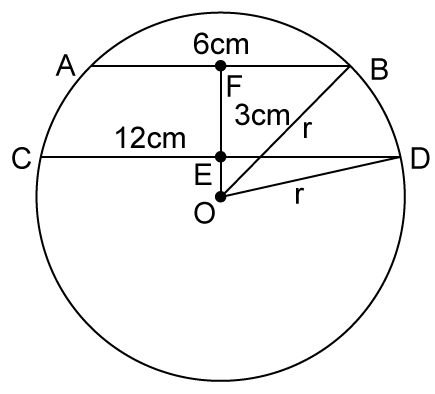
Solution 29
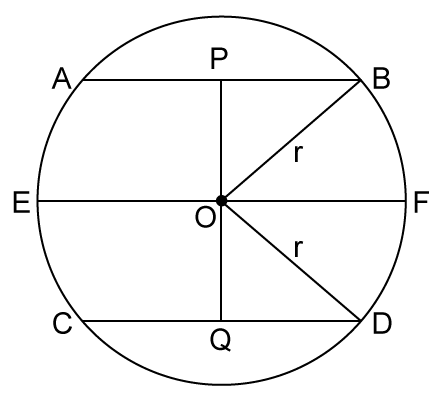
Solution 30
