Class 10 SELINA Solutions Maths Chapter 2 - Banking (Recurring Deposit Accounts)
Students often have issues while computing the lengthy questions of Banking. This is a crucial topic inICSE Class 10 Math as you get a strong base in this area which is helpful for further studies and lifelong applications. Understanding the importance of recurring deposit accounts in mathematical finance is essential. Students are introduced to the concepts of banking, saving, and interest calculations.
For ICSE students who use Math Book by Selina, the Selina Solutions is a guiding light for every chapter, includingBanking– Recurring Deposit Accounts.
Key Concepts Covered
- Explanation of Recurring Deposit Accounts: Learning about the recurring type of deposits basics, their purpose, and how different they are from other account types.
- Interest Calculation: Knowing the formulas and steps of calculation of interest rates on recurring deposits and also about the interest rates.
- Maturity Amount Calculation: Understand the formulae and step-by-step method required to calculate the maturity amount of a recurring deposit.
- Knowing Factors Affecting Maturity Amount: Learn how the maturity amount is affected by variables such as deposit amount, tenure, and interest rates.
- Real-life Applications: Discover practical situations where familiarity with recurring deposit accounts is crucial, such as financial management and attaining savings objectives.
Why Choose Selina Solutions?
You get your trusted companion in Selina Solutions while working on the chapter on Banking– Recurring Deposit Accounts. Let us give you some compelling reasons that will advocate your choosing Selina Solution as your trusted resource:
- Complete Solutions: You can fully understand each idea by using the step-by-step solutions to all the questions and problems included in the chapter.
- Simple and Direct Explanations: Simple explanations that divide difficult ideas into more manageable pieces.
- Exercise and Planning: An array of practice problems and exercises to solidify your comprehension and get you ready for tests.
- Pictorial aids: Pictures and diagrams to help those who learn best visually understand abstract mathematical concepts.
A solid understanding of the chapter is ensured when studying with Selina Solutions. Other options include using sample papers to practise, viewingvideo lessons on important concepts, rehearsingMCQs, and browsing through other study materials.
Banking (Recurring Deposit Accounts) Exercise Ex. 2(A)
Solution 1
Installment per month(P) = Rs. 600
Number of months(n) = 20
Rate of interest (r) = 10% p.a.

The amount that Manish will get at the time of maturity
=Rs (600 x 20)+ Rs 1,050
=Rs 12,000+ Rs 1,050
= Rs 13,050 Ans.
Solution 2
Installment per month(P) = Rs 640
Number of months(n) = 4.5 × 12 = 54
Rate of interest(r)= 12% p.a.

The amount that Manish will get at the time of maturity
=Rs (640 x 54)+ Rs 9,504
=Rs 34,560+ Rs 9,504
= Rs 44,064
Solution 3
For A
Installment per month(P) = Rs 1,200
Number of months(n) = 3 × 12 = 36
Rate of interest(r)= 10% p.a.

The amount that A will get at the time of maturity
=Rs (1,200 x 36)+ Rs 6,660
=Rs 43,200+ Rs 6,660
= Rs 49,860
For B
Installment per month(P) = Rs 1,500
Number of months(n) = 2.5 × 12 = 30
Rate of interest(r)= 10% p.a.

The amount that B will get at the time of maturity
=Rs(1,500 x 30)+ Rs 5,812.50
=Rs 45,000+ Rs 5,812.50
= Rs 50,812.50
Difference between both amounts= Rs 50,812.50 - Rs 49,860
= Rs 952.50
Then B will get more money than A by Rs 952.50 Ans.
Solution 4
Let Installment per month(P) = Rs y
Number of months(n) = 12
Rate of interest(r)= 11%p.a.

Maturity value= Rs (y x 12) + Rs 0.715 y = Rs 12.715 y
Given maturity value= Rs 12,715
Then Rs 12.715 y = Rs 12,715
![]() Ans.
Ans.
Solution 5
Let Installment per month(P) = Rs y
Number of months(n) = 3.5 × 12 = 42
Rate of interest(r) = 12% p.a.

Maturity value= Rs(y x 42) + Rs 9.03y = Rs 51.03y
Given maturity value = Rs 10,206
Then Rs 51.03y = Rs 10206
![]() Ans.
Ans.
Solution 6
(a)
Installment per month(P) = Rs 140
Number of months(n) = 4 × 12 = 48
Let rate of interest(r)= r %p.a.

Maturity value= Rs (140 x 48) + Rs (137.20)r
Given maturity value= Rs 8,092
Then Rs(140 x 48)+Rs (137.20)r = Rs 8,092
![]() 137.20r = Rs 8,092 - Rs 6,720
137.20r = Rs 8,092 - Rs 6,720
![]() r =
r = ![]()
(b)
Installment per month(P) = Rs 300
Number of months(n) = 4 × 12 = 24
Let rate of interest(r)= r %p.a.

Maturity value= Rs (300 x 24)+Rs(75)r
Given maturity value = Rs 7,725
Then Rs(300 x 24) + Rs(75)r = Rs 7,725
![]() 75 r = Rs 7,725 - Rs 7,200
75 r = Rs 7,725 - Rs 7,200
![]() r =
r = ![]()
Solution 7
Installment per month(P) = Rs 150
Number of months(n) = 8
Rate of interest(r)= 8% p.a.

The amount that Manish will get at the time of maturity
=Rs (150 x 8)+ Rs 36
=Rs 1,200+ Rs 36
= Rs 1,236 Ans.
Solution 8
Installment per month(P) = Rs 350
Number of months(n) = 12 + 3 = 15
Let rate of interest(r)= r %p.a.

Maturity value= Rs (350 x 15) + Rs (35)r
Given maturity value= Rs 5,565
Then Rs (350 x 15) + Rs (35)r = Rs 5,565
![]() 35r = Rs 5,565 - Rs 5,250
35r = Rs 5,565 - Rs 5,250
![]() r =
r = ![]()
Solution 9
Installment per month(P) = Rs 1,200
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.

Maturity value= Rs (1,200 x n) + Rs 4n (n + 1)= Rs (1200n + 4n2 + 4n)
Given maturity value= Rs 12,440
Then 1200n + 4n2 + 4n = 12,440
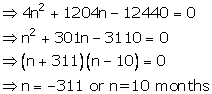
Then number of months = 10 Ans.
Solution 10
Installment per month(P) = Rs 300
Number of months(n) = n
Let rate of interest(r)= 12 %p.a.

Maturity value= Rs (300 x n) + Rs 1.5n(n + 1)
= Rs (300n + 1.5n2 + 1.5n)
Given maturity value = Rs 8,100
Then 300n + 1.5n2 + 1.5n = 8,100
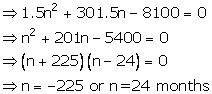
Then time = 2 years
Solution 11
(i)
Maturity value = Rs 67,500
Money deposited = Rs 2,500 x 24 = Rs 60,000
Then total interest earned = Rs 67,500 - Rs 60,000 = Rs 7,500 Ans.
(ii)
Installment per month(P) = Rs 2,500
Number of months(n) = 24
Let rate of interest(r)= r %p.a.

Then 625 r = 7500
![]()
Banking (Recurring Deposit Accounts) Exercise Ex. 2(B)
Solution 1
Installment per month(P) = Rs 600
Number of months(n) = 4 × 12 = 48
Rate of interest(r)= 8%p.a.
_21Maynewformat_files/20140521155159_image015.gif)
The amount that Manish will get at the time of maturity
=Rs (600 x 48)+ Rs 4,704
=Rs 28,800+ Rs 4,704
= Rs 33,504 Ans.
Solution 2
Installment per month(P) = Rs 80
Number of months(n) = 18
Let rate of interest(r)= r % p.a.
_21Maynewformat_files/20140521155159_image017.gif)
Maturity value= Rs (80 x 18) + Rs (11.4r)
Given maturity value= Rs 1,554
Then Rs (80 x 18)+Rs (11.4r) = Rs 1,554
![]() 11.4r = Rs 1,554 - Rs 1,440
11.4r = Rs 1,554 - Rs 1,440
![]()
Solution 3
Installment per month(P) = Rs 400
Number of months(n) = n
Let rate of interest(r)= 8 %p.a.
_21Maynewformat_files/20140521155159_image024.gif)
Maturity value= Rs (400 x n)+![]()
Given maturity value= Rs 16,176
Then Rs (400 x n)+![]() = Rs 16,176
= Rs 16,176
![]() 1200n + 4n2 + 4n = Rs 48,528
1200n + 4n2 + 4n = Rs 48,528
![]() 4n2 + 1204n = Rs 48,528
4n2 + 1204n = Rs 48,528
![]() n2 + 301n - 12132 = 0
n2 + 301n - 12132 = 0
![]() (n + 337)(n - 36)=0
(n + 337)(n - 36)=0
![]() n = -337 or n = 36
n = -337 or n = 36
Then number of months = 36 months = 3 years Ans.
Solution 4
Let installment per month = Rs P
Number of months(n) = 2 × 12 = 24
Rate of interest = 8%p.a.
_21Maynewformat_files/20140521155159_image035.gif)
Maturity value= Rs (P x 24) + Rs 2P = Rs 26P
Given maturity value = Rs 30,000
_21Maynewformat_files/20140521155159_image037.gif)
Solution 5
Let the monthly instalment be P
Interest = Rs. 8,325
Rate of interest = 7.5%
Time = 3 years = 36 months
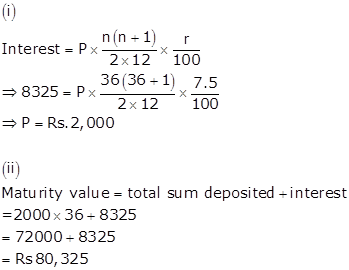
Solution 6
Installment per month(P) = Rs 900
Number of months(n) = 48
Let rate of interest(r) = r %p.a.

Maturity value= Rs (900 x 48) + Rs (882)r
Given maturity value = Rs 52,020
Then Rs (900 x 48) + Rs(882)r = Rs 52,020
![]() 882r = Rs 52,020 - Rs 43,200
882r = Rs 52,020 - Rs 43,200
![]() r =
r = ![]()
Solution 7
Installment per month(P) = Rs 1,800
Number of months(n) = 4 × 12 = 48
Let rate of interest(r)= r %p.a.
_21Maynewformat_files/20140521155159_image049.gif)
Maturity value= Rs (1,800 x 48) + Rs(1,764)r
Given maturity value= Rs 1,08,450
Then Rs (1,800 x 48) + Rs(1764)r = Rs 1,08,450
![]() 1764r = Rs 1,08,450 - Rs 86,400
1764r = Rs 1,08,450 - Rs 86,400
![]() r =
r = ![]()
Solution 8
Let the value of the monthly installment be Rs. P.

Thus, the value of his monthly installment is Rs. 200.
Solution 9

Solution 10

Solution 11
Interest, I = Rs. 1,200
Time, n = 2 years = 2 × 12 = 24 months
Rate, r = 6%
(i) To find: Monthly installment, P
Now,

So, the monthly installment is Rs. 800.
(ii) Total sum deposited = P × n = Rs. 800 × 24 = Rs. 19,200
∴ Amount of maturity = Total sum deposited + Interest on it
= Rs. (19,200 + 1,200)
= Rs. 20,400

