Class 10 SELINA Solutions Maths Chapter 10 - Arithmetic Progression
ICSE board, or Indian Certificate of Secondary Education Board, is one of the most reputed boards in the country and is accepted all around the globe. It has a more comprehensive syllabus compared to other boards and focuses on both academic excellence and the holistic development of the students. The ICSE curriculum builds a strong foundation and helps the students develop critical thinking skills and gain practical knowledge. But to excel in their future academic and professional pursuits, students need more than just classroom learning. Selina Solutions provides complete coverage and solutions for various subjects.
When it comes to ICSE Class 10 Math, the chapter Arithmetic Progressions holds a lot of importance. It requires students to use basic mathematical operations, identify patterns, calculate terms and sums, explore number patterns, and develop sequencing skills. Students must simplify expressions and use their mathematical reasoning, problem-solving abilities, and pattern recognition skills to analyze and manipulate sequences of numbers with a constant difference. To solve such questions, students need a solid understanding of mathematical concepts and the application of appropriate techniques.
Selina Solutions offer comprehensive and detailed solutions to the problems in the Arithmetic Progressions chapter. They cover all the topics and concepts from the ICSE Class 10 Mathematics syllabus. Explanations and step-by-step answers ensure that the students understand the underlying principles and techniques required to solve arithmetic progression problems.
Students get exposed to different problems, from simple to complex arithmetic progressions. This allows them to practice various fractions, decimals, percentages, ratios, proportions, and more. Thus, the solutions offer a range of examples which helps students build proficiency, self-assess their progress and recognise concepts that require further practice or clarification.
TopperLearning offers a conceptualised learning experience and has thus become the country’s leading online education program. Students can find Selina Solutions for Maths, Chemistry, Physics and Biology for their respective classes. Moreover, its extensive study materials, such as textbook solutions, sample papers, video lessons, practice tests, revision notes, and more prepared by a highly experienced and qualified team, ensure that the quality content elevates the students’ learning outcomes.
Arithmetic Progression Exercise Ex. 10(A)
Solution 1

Solution 2
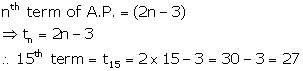
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11
The given A.P. is 1, 4, 7, 10, ……….
Solution 12
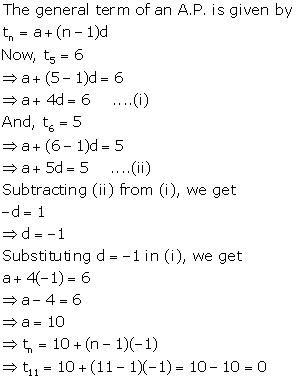
Solution 13

Solution 14

Solution 15

Solution 16
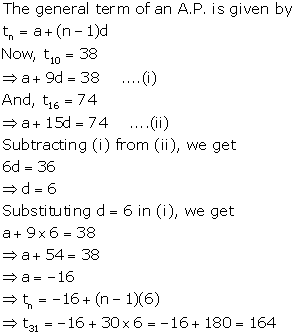
Solution 17

Solution 18
For a given A.P.,
Number of terms, n = 60
First term, a = 7
Last term, l = 125
⇒ t60 = 125
⇒ a + 59d = 125
⇒ 7 + 59d = 125
⇒ 59d = 118
⇒ d = 2
Hence, t31 = a + 30d = 7 + 30(2) = 7 + 60 = 67
Solution 19
Let 'a' be the first term and 'd' be the common difference of the given A.P.
t4 + t8 = 24 (given)
⇒ (a + 3d) + (a + 7d) = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ….(i)
And,
t6 + t10 = 34 (given)
⇒ (a + 5d) + (a + 9d) = 34
⇒ 2a + 14d = 34
⇒ a + 7d = 17 ….(ii)
Subtracting (i) from (ii), we get
2d = 5
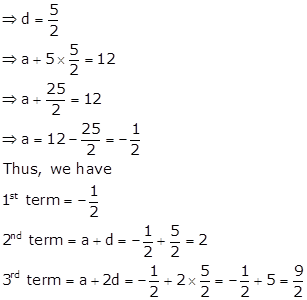
Solution 20
Let 'a' be the first term and 'd' be the common difference of the given A.P.
Now, t3 = 5 (given)
⇒ a + 2d = 5 ….(i)
And,
t7 = 9 (given)
⇒ a + 6d = 9 ….(ii)
Subtracting (i) from (ii), we get
4d = 4
⇒ d = 1
⇒ a + 2(1) = 5
⇒ a = 3
Hence, 17th term = t17 = a + 16d = 3 + 16(1) = 19
Arithmetic Progression Exercise Ex. 10(B)
Solution 1

Solution 2

Solution 3

Solution 4
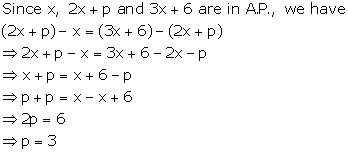
Solution 5

Solution 6

Solution 7
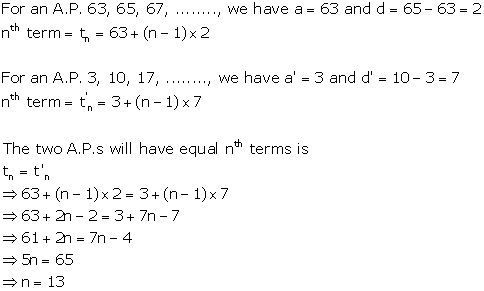
Solution 8

Solution 9
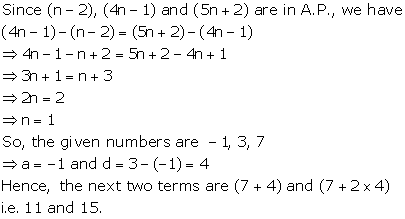
Solution 10
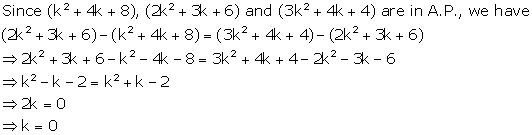
Solution 11

Solution 12
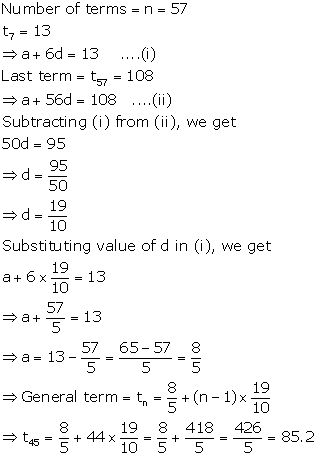
Solution 13

Solution 14

Solution 15
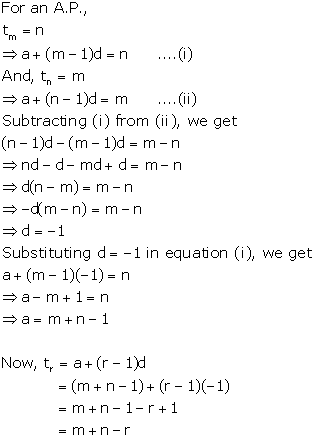
Solution 16

Arithmetic Progression Exercise Ex. 10(C)
Solution 1

Solution 2
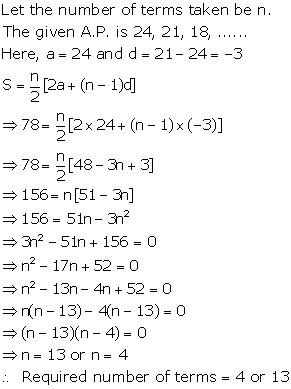
Solution 3

Solution 4(i)

Solution 4(ii)

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13
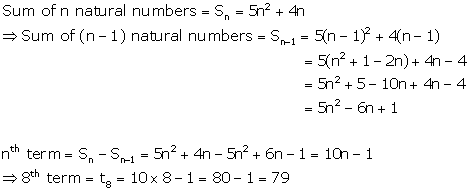
Solution 14

Arithmetic Progression Exercise Ex. 10(D)
Solution 1
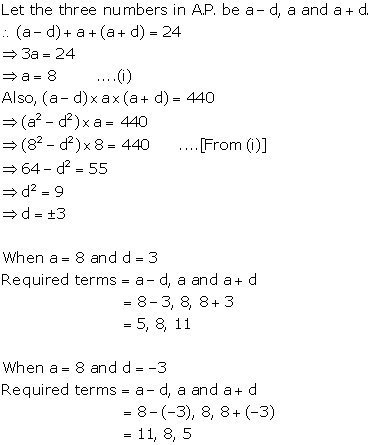
Solution 2

Solution 3

Solution 4
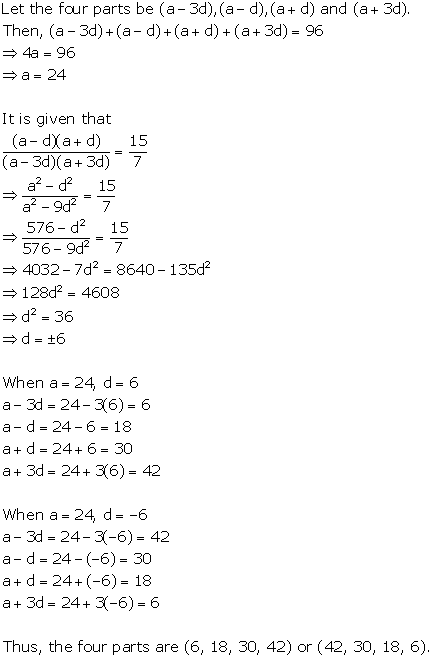
Solution 5
We know that,
Sum of n terms of an A.P = ![]()
Let the first term be 2x and the last term be 3x.
∴ Sum of 5 terms of an A.P = ![]()
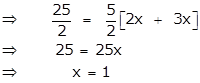
First term = 2x =2 × 1 = 2 and the last term = 3x = 3 × 1 = 3
nth term of an A.P. is given by
tn = a + (n - 1)d
⇒ a5 = 2 + (5 - 1)d
⇒ 3 = 2 + 4d
⇒ 1 = 4d
⇒ d = ![]() = 0.25
= 0.25
Therefore the five numbers in an A.P are 2, 2.25, 2.50, 2.75 and 3.
Solution 6

Solution 7
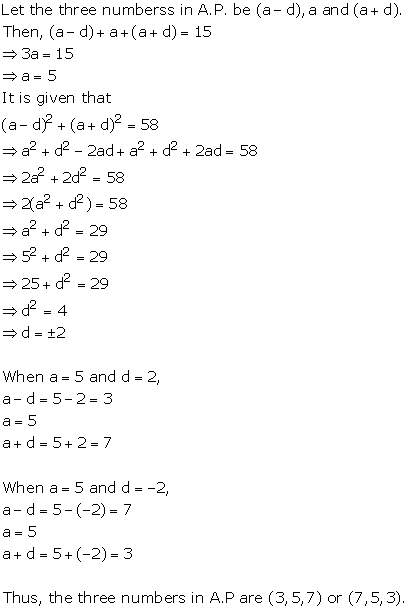
Solution 8
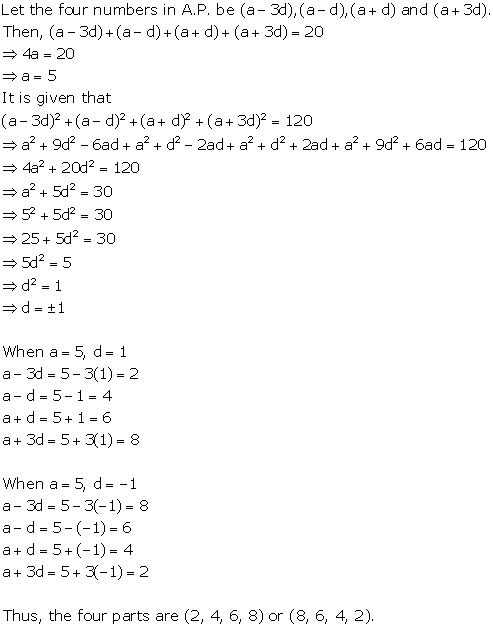
Solution 9
![]()
Solution 10

Solution 11
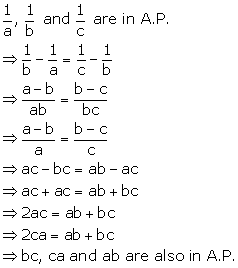
Arithmetic Progression Exercise Ex. 10(E)
Solution 1
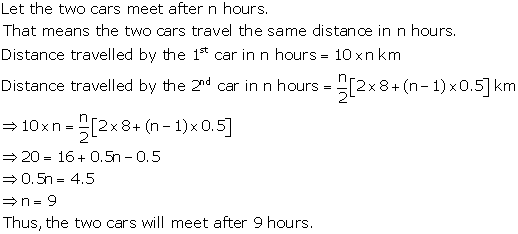
Solution 2
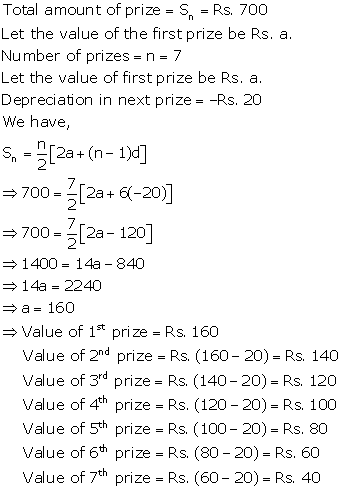
Solution 3

Solution 4
Since the production increases uniformly by a fixed number every year, he sequence formed by the production in different years is an A.P.
Let the production in the first year = a
Common difference = Number of units by which the production increases every year = d

Solution 5
Total amount of loan = Rs. 1,18,00
First instalment = a = Rs. 1000
Increase in instalment every month = d= Rs. 100
30th instalment = t30
= a + 29d
= 1000 + 29 × 100
= 1000 + 2900
= Rs. 3900
Now, amount paid in 30 instalment = S30

= 15 × 4900
= Rs. 73, 500
∴ Amount of loan to be paid after the 30th instalment
= Rs. (1,18,000 - 73500)
= Rs. 44,500
Arithmetic Progression Exercise Ex. 10(F)
Solution 1
Let 'a' be the first term and 'd' be the common difference of the given A.P.
Now, t6 = 16 (given)
⇒ a + 5d = 16 ….(i)
And,
t14 = 32 (given)
⇒ a + 13d = 32 ….(ii)
Subtracting (i) from (ii), we get
8d = 16
⇒ d = 2
⇒ a + 5(2) = 16
⇒ a = 6
Hence, 36th term = t36 = a + 35d = 6 + 35(2) = 76
Solution 2

Solution 3
For a given A.P.,
Number of terms, n = 50
3rd term, t3 = 12
⇒ a + 2d = 12 ….(i)
Last term, l = 106
⇒ t50 = 106
⇒ a + 49d = 106 ….(ii)
Subtracting (i) from (ii), we get
47d = 94
⇒ d = 2
⇒ a + 2(2) = 12
⇒ a = 8
Hence, t29 = a + 28d = 8 + 28(2) = 8 + 56 = 64
Solution 4
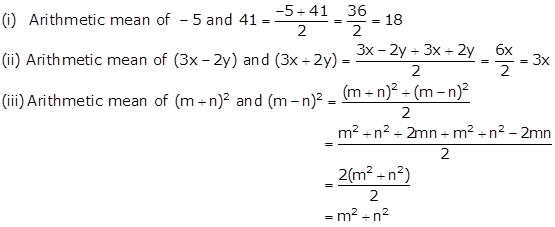
Solution 5
Here,
First term, a = 4
Common difference, d = 6 - 4 = 2
n = 10
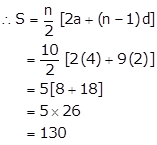
Solution 6
Here,
First term, a = 3
Last term, l = 57
n = 20
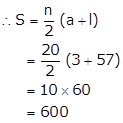
Solution 7
Here, we find that
15 - 18 = 12 - 15 = -3
Thus, the given series is an A.P. with first term 18 and common difference -3.
Let the number of term to be added be 'n'.
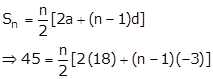
⇒ 90 = n[36 - 3n + 3]
⇒ 90 = n[39 - 3n]
⇒ 90 = 3n[13 - n]
⇒ 30 = 13n - n2
⇒ n2 - 13n + 30 = 0
⇒ n2 - 10n - 3n + 30 = 0
⇒ n(n - 10) - 3(n - 10) = 0
⇒ (n - 10)(n - 3) = 0
⇒ n - 10 = 0 or n - 3 = 0
⇒ n = 10 or n = 3
Thus, required number of term to be added is 3 or 10.
Solution 8
tn = 8 - 5n
Replacing n by (n + 1), we get
tn+1 = 8 - 5(n + 1) = 8 - 5n - 5 = 3 - 5n
Now,
tn+1 - tn = (3 - 5n) - (8 - 5n) = -5
Since, (tn+1 - tn) is independent of n and is therefore a constant.
Hence, the given sequence is an A.P.
Solution 9
The given sequence is 1, -1, -3, …..
Now,
1 - 3 = -1 - 1 = -3 - (-1) = -2
Hence, the given sequence is an A.P. with first term a = 3 and common difference d = -2.
The general term (nth term) of an A.P. is given by
tn = a + (n - 1)d
= 3 + (n - 1)(-2)
= 3 - 2n + 2
= 5 - 2n
Hence, 23rd term = t23 = 5 - 2(23) = 5 - 46 = -41
Solution 10
The given sequence is 3, 8, 13, …..
Now,
8 - 3 = 13 - 8 = 5
Hence, the given sequence is an A.P. with first term a = 3 and common difference d = 5.
Let the nth term of the given A.P. be 78.
⇒ 78 = 3 + (n - 1)(5)
⇒ 75 = 5n - 5
⇒ 5n = 80
⇒ n = 16
Thus, the 16th term of the given sequence is 78.
Solution 11
The given sequence is 11, 8, 5, 2, …..
Now,
8 - 11 = 5 - 8 = 2 - 5 = -3
Hence, the given sequence is an A.P. with first term a = 11 and common difference d = -3.
The general term of an A.P. is given by
tn = a + (n - 1)d
⇒ -150 = 11 + (n - 1)(-5)
⇒ -161 = -5n + 5
⇒ 5n = 166
![]()
The number of terms cannot be a fraction.
So, clearly, -150 is not a term of the given sequence.
Solution 12

Solution 13

Solution 14

Solution 15
Let 'a' be the first term and 'd' be the common difference of the given A.P.
Given,
S14 = 1050
![]()
⇒ 7[2a + 13d] = 1050
⇒ 2a + 13d = 150
⇒ a + 6.5d = 75 ….(i)
And, t14 = 140
⇒ a + 13d = 140 ….(ii)
Subtracting (i) from (ii), we get
6.5d = 65
⇒ d = 10
⇒ a + 13(10) = 140
⇒ a = 10
Thus, 20th term = t20 = 10 + 19d = 10 + 19(10) = 200
Solution 16
nth term of an A.P. is given by tn= a + (n - 1) d.
⇒ t25 = a + (25 - 1)d = a + 24d and
t9 = a + (9 - 1)d = a + 8d
According to the condition in the question, we get
t25 = t9 + 16
⇒ a + 24d = a + 8d + 16
⇒ 16d = 16
⇒ d = 1
Solution 17
Let a and d be the first term and common difference respectively.
⇒(m + n)th term = a + (m + n - 1)d …. (i) and
(m - n)th term = a + (m - n - 1)d …. (ii)
From (i) + (ii), we get
(m + n)th term + (m - n)th term
= a + (m + n - 1)d + a + (m - n - 1)d
= a + md + nd - d + a + md - nd - d
= 2a + 2md - 2d
= 2a + (m - 1)2d
= 2[ a + (m - 1)d]
= 2 × mthterm
Hence proved.
Solution 18
In the first A.P. 58, 60, 62,....
a = 58 and d = 2
tn = a + (n - 1)d
⇒ tn = 58 + (n - 1)2 …. (i)
In the first A.P. -2, 5, 12, ….
a = -2 and d = 7
tn = a + (n - 1)d
⇒ tn= -2 + (n - 1)7 …. (ii)
Given that the nth term of first A.P is equal to the nth term of the second A.P.
⇒58 + (n - 1)2 = -2 + (n - 1)7 … from (i) and (ii)
⇒58 + 2n - 2 = -2 + 7n - 7
⇒ 65 = 5n
⇒ n = 15
Solution 19
Here a = 105 and d = 101 - 105 = -4
Let an be the first negative term.
⇒ an < 0
⇒ a + (n - 1)d < 0
⇒ 105 + (n - 1)(-4)<0
⇒ 105 - 4n + 4 <0
⇒ 109 - 4n < 0
⇒ 109 <4n
⇒ 27.25 < n
The value of n = 28.
Therefore 28th term is the first negative term of the given A.P.
Solution 20
The first three digit number which is divisible by 7 is 105 and the last digit which is divisible by 7 is 994.
This is an A.P. in which a = 105, d = 7 and tn = 994.
We know that nth term of A.P is given by
tn = a + (n - 1)d.
⇒ 994 = 105 + (n - 1)7
⇒ 889 = 7n - 7
⇒ 896 = 7n
⇒ n = 128
∴ There are 128 three digit numbers which are divisible by 7.
Solution 21
Let the three parts of 216 in A.P be (a - d), a, (a + d).
⇒a - d + a + a + d = 216
⇒ 3a = 216
⇒ a = 72
Given that the product of the two smaller parts is 5040.
⇒a(a - d ) = 5040
⇒ 72(72 - d) = 5040
⇒ 72 - d = 70
⇒ d = 2
∴ a - d = 72 - 2 = 70, a = 72 and a + d = 72 + 2 = 74
Therefore the three parts of 216 are 70, 72 and 74.
Solution 22
We have 2n2 - 7,
Substitute n = 1, 2, 3, … , we get
2(1)2 - 7, 2(2)2 - 7, 2(3)2 - 7, 2(4)2 - 7, ….
-5, 1, 11, ….
Difference between the first and second term = 1 - (-5) = 6
And Difference between the second and third term = 11 - 1 = 10
Here, the common difference is not same.
Therefore the nth term of an A.P can't be 2n2 - 7.
Solution 23
Here a = 14 , d = 7 and tn = 168
tn = a + (n - 1)d
⇒ 168 = 14 + (n - 1)7
⇒ 154 = 7n - 7
⇒ 154 = 7n - 7
⇒ 161 = 7n
⇒ n = 23
We know that,

Therefore the sum of the A.P., 14, 21, 28, …, 168 is 2093.
Solution 24
Here a = 20 and S7 = 2100
We know that,
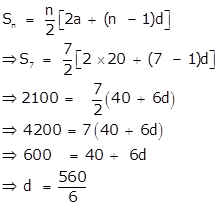
To find: t31 =?
tn = a + (n - 1)d
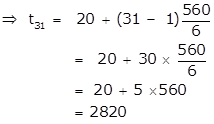
Therefore the 31st term of the given A.P. is 2820.
Solution 25
First we will reverse the given A.P. as we have to find the sum of last 8 terms of the A.P.
58, …., -8, -10, -12.
Here a = 58 , d = -2
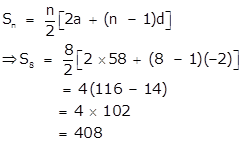
Therefore the sum of last 8 terms of the A.P. -12, -10, -8, ……, 58 is 408.


