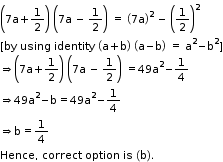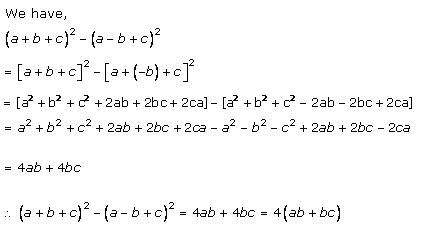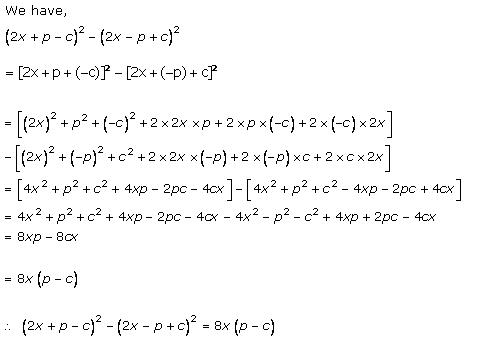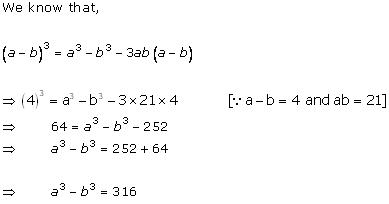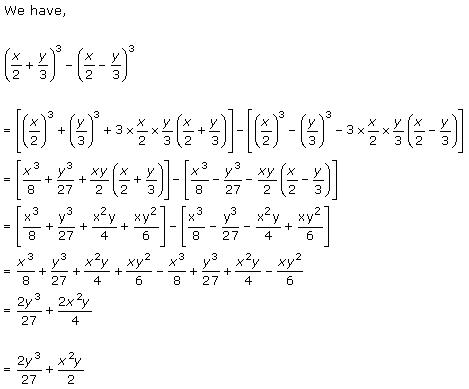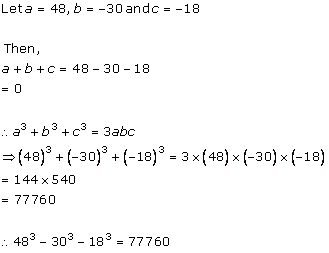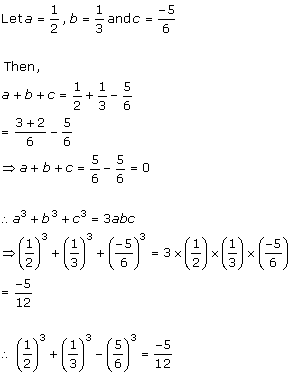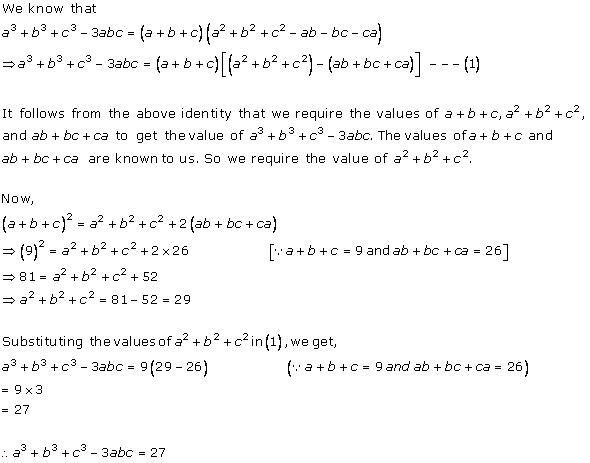Class 9 RD SHARMA Solutions Maths Chapter 4 - Algebraic Identities
Algebraic Identities Exercise Ex. 4.1
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)
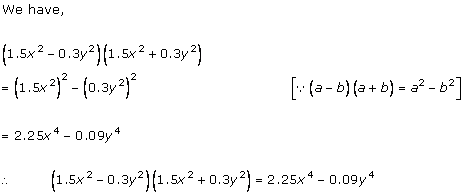
Solution 2(i)
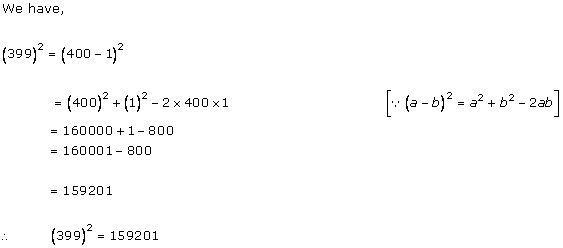
Solution 2(ii)
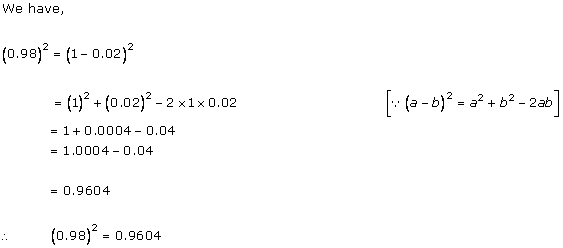
Solution 2(iii)

Solution 2(iv)

Solution 3(i)
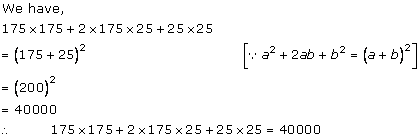
Solution 3(ii)
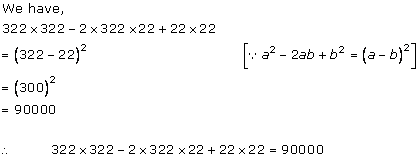
Solution 3(iii)
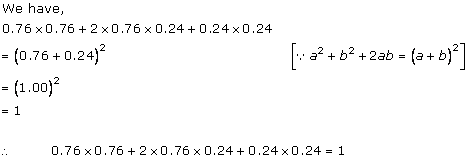
Solution 3(iv)

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10(i)

Solution 10(ii)

Solution 11

Solution 12

Solution 13(i)
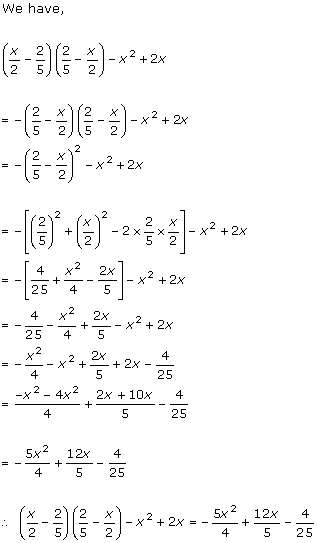
Solution 13(ii)

Solution 13(iii)

Solution 13(iv)

Solution 14
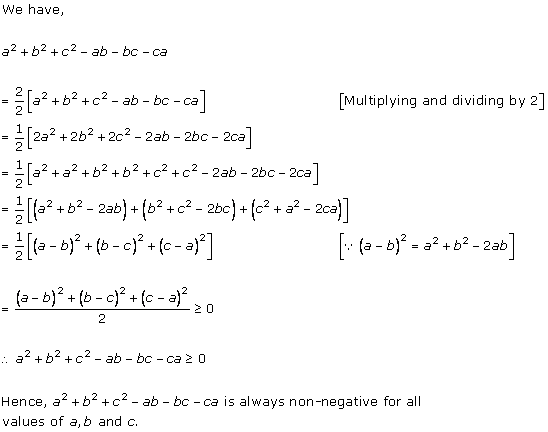
Algebraic Identities Exercise Ex. 4.2
Solution 1(i)

Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 1(vii)

Solution 1(viii)
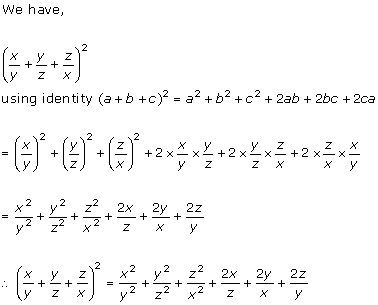
Solution 1(ix)
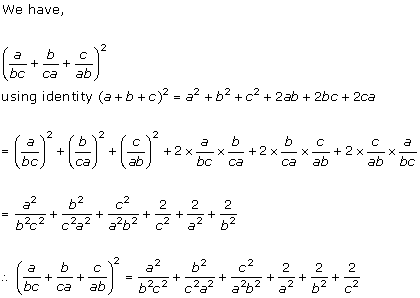
Solution 1 (x)
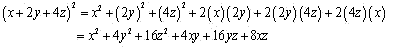
Solution 1 (xi)

Solution 1 (xii)
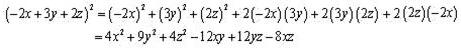
Solution 2

Solution 3

Solution 4

Solution 5

Solution 6(i)
Solution 6(ii)
Solution 6(iii)

Solution 6(iv)
Solution 6(v)
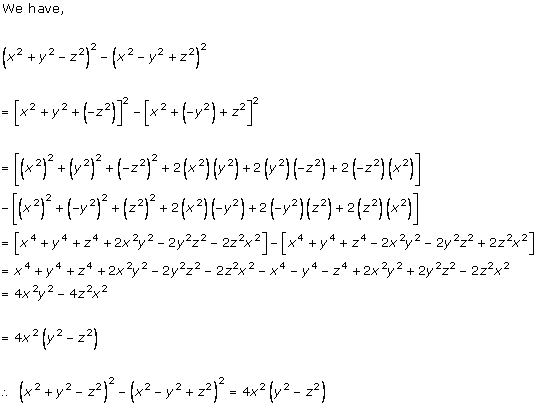
Solution 7(i)

Solution 7(ii)

Solution 7(iii)
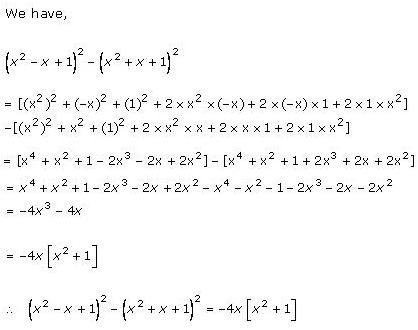
Algebraic Identities Exercise Ex. 4.3
Solution 1(i)

Solution 1(ii)
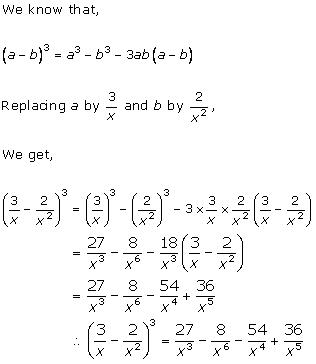
Solution 1(iii)

Solution 1(iv)

Solution 2

Solution 3
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11(i)

Solution 11(ii)

Solution 11(iii)

Solution 11(iv)

Solution 11(v)
Solution 11(vi)

Solution 12(i)

Solution 12(ii)

Solution 12(iii)

Solution 12(iv)

Solution 13
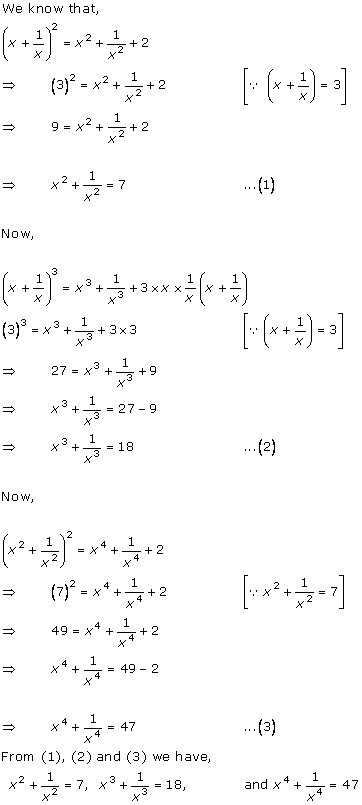
Solution 14(i)

Solution 14(ii)

Solution 15

Solution 16

Solution 17(i)

Solution 17(ii)
Solution 17(iii)

Solution 17(iv)

Solution 18

Solution 19

Algebraic Identities Exercise Ex. 4.4
Solution 1 (i)
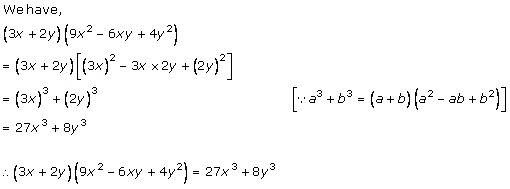
Solution 1 (ii)
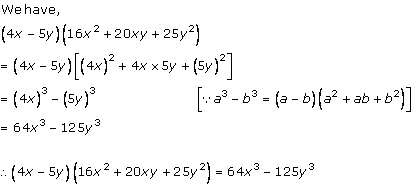
Solution 1 (iii)
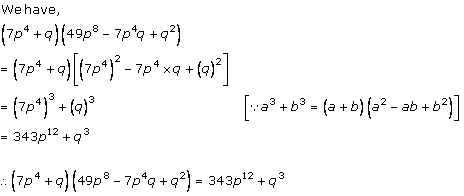
Solution 1 (iv)
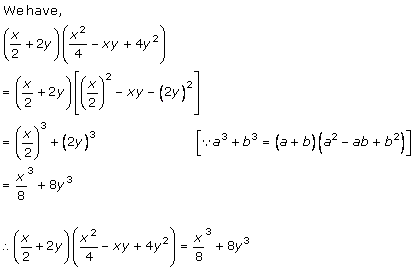
Solution 1 (v)
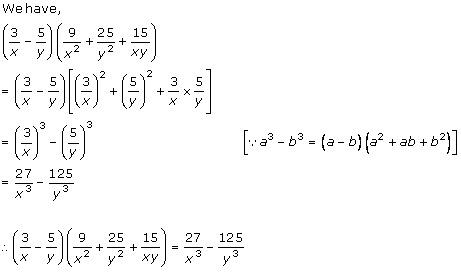
Solution 1 (vi)
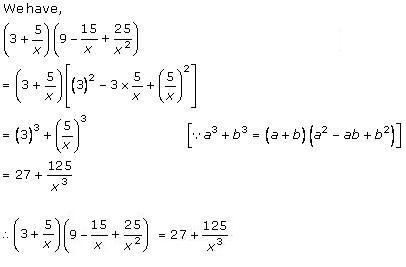
Solution 1 (vii)
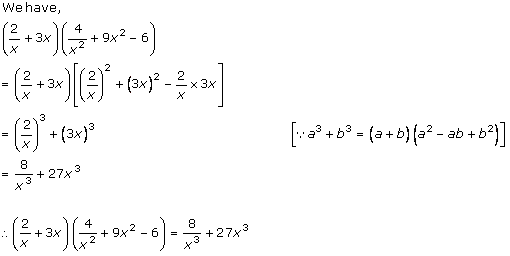
Solution 1 (viii)
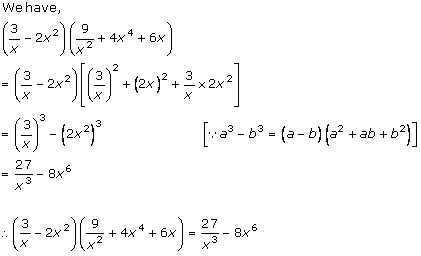
Solution 1 (ix)
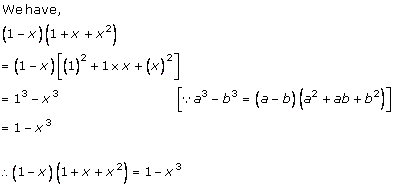
Solution 1 (x)

Solution 1 (xi)
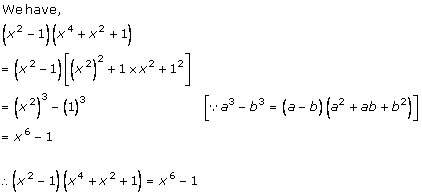
Solution 1 (xii)
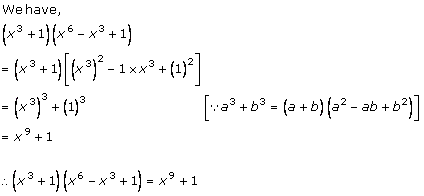
Solution 2 (i)
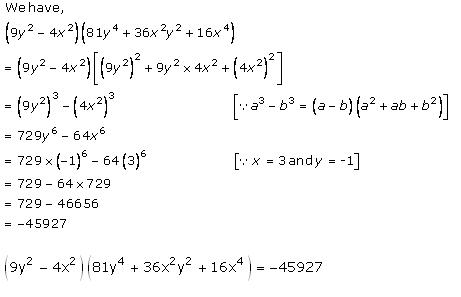
Solution 2 (ii)
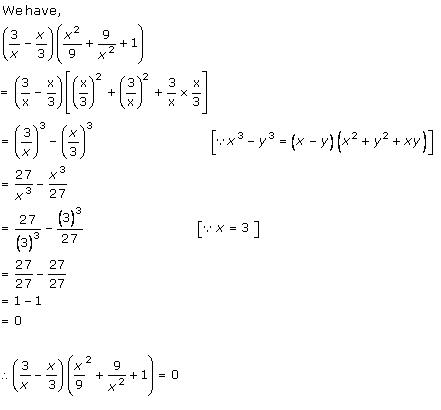
Solution 2 (iii)
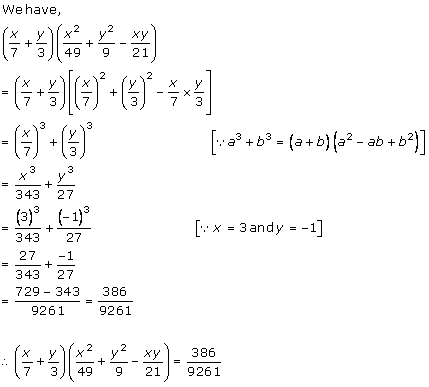
Solution 2 (iv)
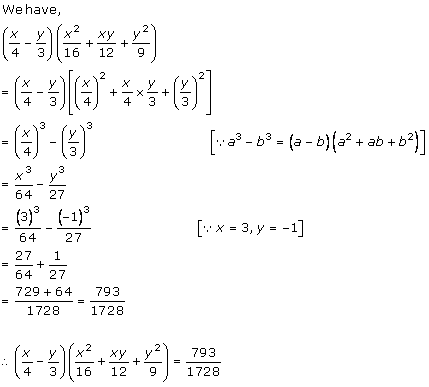
Solution 2 (v)
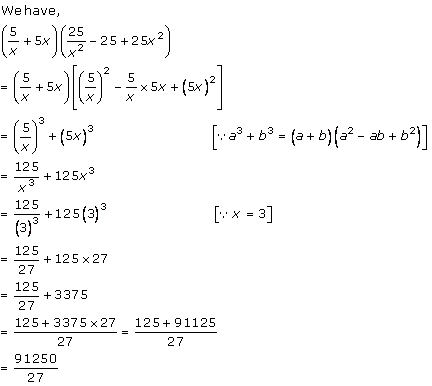
Solution 3

Solution 4
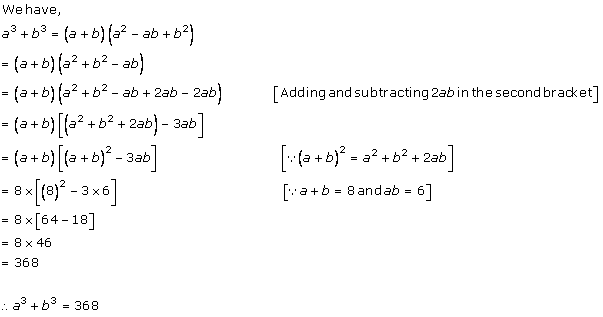
Solution 5
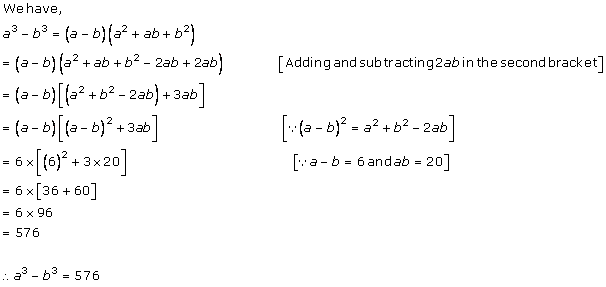
Solution 6 (i)
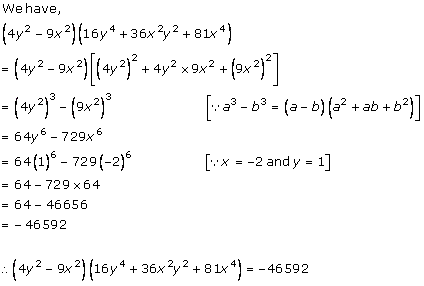
Solution 6 (ii)
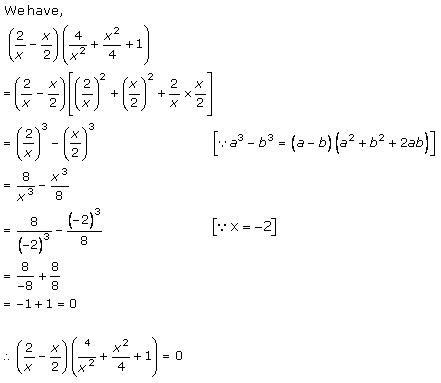
Solution 6 (iii)

Algebraic Identities Exercise Ex. 4.5
Solution 1 (i)

Solution 1 (ii)
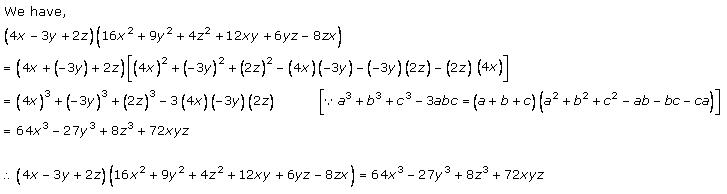
Solution 1 (iii)
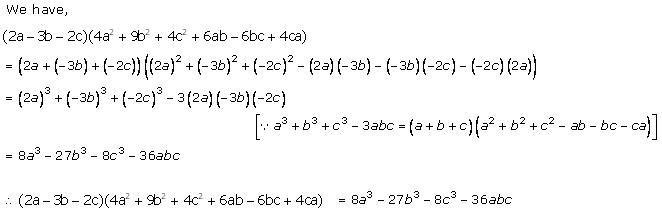
Solution 1 (iv)
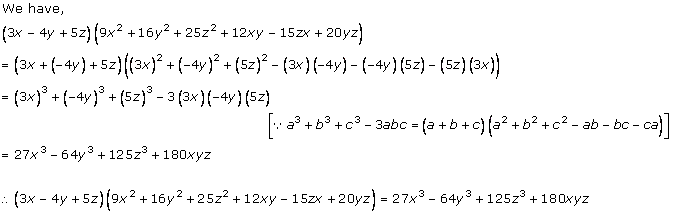
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
Solution 2(iv)
Solution 3
Solution 4
Solution 5
Algebraic Identities Exercise 4.30
Solution 1

Solution 2
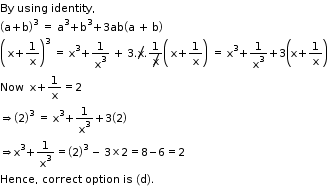
Solution 3
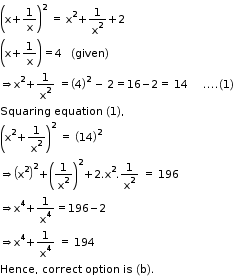
Solution 4
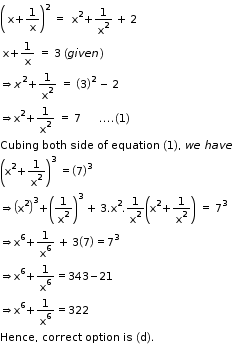
Solution 5

Solution 6
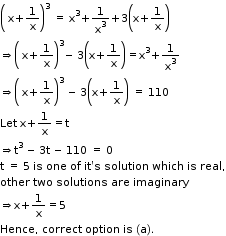
Solution 7
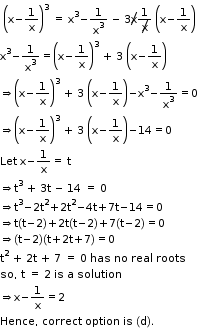
Solution 8
We know that (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
Here, a + b + c = 9, ab + bc + ca = 23
Thus, we have
(9)2 = a2 + b2 + c2 + 2(23)
81 = a2 + b2 + c2 + 46
a2 + b2 + c2 = 81 - 46
a2 + b2 + c2 = 35
Hence, correct option is (a).
Solution 9
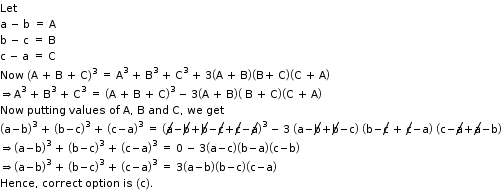
Solution 10

Solution 11
a - b = -8
(a - b)2 = 64
a2 + b2 - 2ab = 64
a2 + b2 - 2ab + 3ab = 64 + 3ab
a2 + b2 + ab = 64 + 3(-12)
a2 + b2 + ab = 64 - 36
a2 + b2 + ab = 28
Now a3 - b3 = (a - b)(a2 + b2 + ab)
= (-8)(28)
= -224
Hence, correct option is (c).
Algebraic Identities Exercise 4.31
Solution 12
Volume of a cuboid of side a, b and c = abc
Now, Volume = 3x2 - 27 (given)
abc = 3(x2 - 9)
abc = 3(x - 3)(x + 3)
So, possible dimensions are 3, x - 3 and x + 3
Hence, correct option is (b).
Solution 13
Given expression is 75 × 75 + 2 × 75 × 25 + 25 × 25
Let 75 = a and 25 = b
Then, we have
a × a + 2 × a × b + b × b
= a2 + 2ab + b2
= (a + b)2
= (75 + 25)2
= (100)2
= 10000
Hence, correct option is (a).
Solution 14
(x - y)(x + y) = x2 - y2 [by identity (a + b)(a - b) = a2 - b2]
(x2 - y2)(x2 + y2) = x4 - y4
(x4 - y4)(x4 + y4) = x8 - y8
Now,
(x - y)(x + y)(x2 + y2)(x4 + y4)
= (x2 - y2)(x2 + y2)(x4 + y4)
= (x4 - y4)(x4 + y4)
= x8 - y8
Hence, correct option is (b).
Solution 15

Solution 16
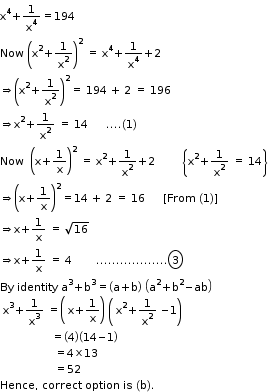
Solution 17
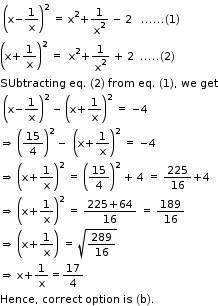
Solution 18
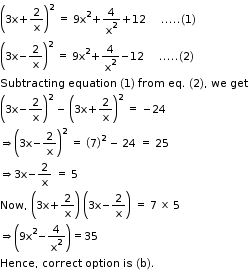
Solution 19
a2 + b2 + c2 - ab - bc - ca = 0
Multiplying by 2 on both the sides, we have
2(a2 + b2 + c2 - ab - bc - ca) = 0
2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca = 0
a2 + a2 + b2 + b2 + c2 + c2 - 2ab - 2bc - 2ca = 0
(a2 + b2 - 2ab) + (b2 + c2 - 2bc) + (a2 + c2 - 2ac) = 0
(a - b)2 + (b - c)2 + (a - c)2 = 0
(a - b)2 = 0, (b - c)2 = 0, (a - c)2 = 0
(a - b) = 0, (b - c) = 0, (a - c) = 0
a = b, b = c, a = c
or we can say a = b = c
Hence, correct option is (d).
Solution 20

Solution 21
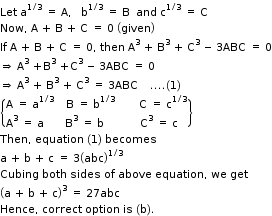
Solution 22
Given, a + b + c = 9
Hence, (a + b + c)2 = 81
So, a2 + b2 + c2 + 2ab + 2bc + 2ca = 81
i.e. a2 + b2 + c2 + 2(ab + bc + ca) = 81
i.e. a2 + b2 + c2 + 2(23) = 81
i.e. a2 + b2 + c2 = 81 - 46 = 35
Now, a3 + b3 + c3 - 3abc
= (a + b + c)(a2 + b2 + c2 - ab - bc - ca)
= (a + b + c)[(a2 + b2 + c2) - (ab + bc + ca)]
= (9)[35 - 23]
= 9 × 12
= 108
Hence, correct option is (a).
Solution 23
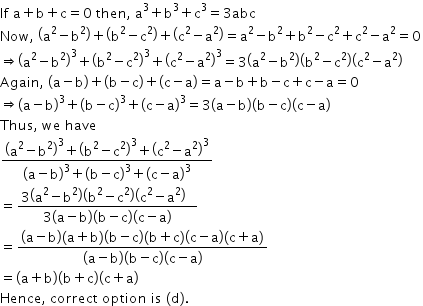
Algebraic Identities Exercise 4.32
Solution 24

Solution 25
Given expression is (x2 - 1)(x4 + x2 + 1)
Let x2 = A and 1 = B
Then, we have
(A - B)(A2 + AB + B2)
= A3 - B3
= (x2)3 - (1)3
= x6 - 1
Hence, correct option is (c).
Solution 26
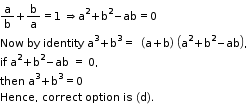
Solution 27